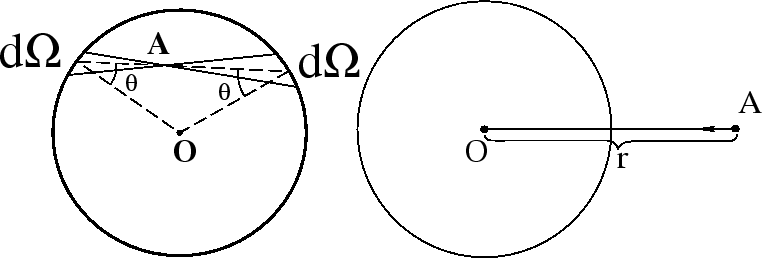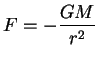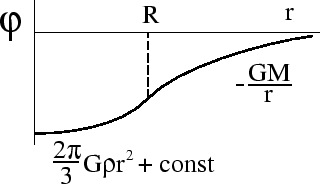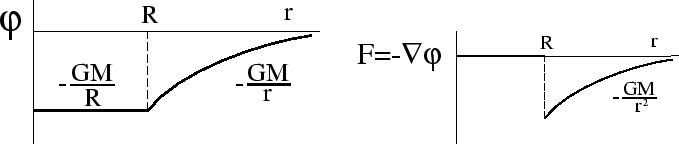<< 1.2 Vektornoe pole uskorenii ... | Oglavlenie | 1.4 Energiya gravitacionnogo vzaimodeistviya >>
1.3 Sfericheski-simmetrichnye polya tyagoteniya, polnaya i tekushaya massy zvezd, eilerovy i lagranzhevy koordinaty
Rassmotrim tonkii sfericheskii sloi s radiusom ![]() , tolshinoi
, tolshinoi
![]() i
poverhnostnoi plotnost'yu
i
poverhnostnoi plotnost'yu ![]() [g/sm
[g/sm![]() ]. Naidem silu prityazheniya so storony sfery,
kotoraya deistvuet na probnuyu chasticu edinichnoi massy, pomeshennuyu v kakoi-libo tochke
]. Naidem silu prityazheniya so storony sfery,
kotoraya deistvuet na probnuyu chasticu edinichnoi massy, pomeshennuyu v kakoi-libo tochke
![]() vnutri sfery. Iz ris.2
naglyadno vidno, chto sily prityazheniya dvuh elementov
mass, vyrezannyh na sfere telesnym uglom
vnutri sfery. Iz ris.2
naglyadno vidno, chto sily prityazheniya dvuh elementov
mass, vyrezannyh na sfere telesnym uglom ![]() , odinakovy po velichine i
protivopolozhny po napravleniyu. Bolee blizkii k tochke
, odinakovy po velichine i
protivopolozhny po napravleniyu. Bolee blizkii k tochke ![]() element
element ![]() imeet
men'shuyu massu, i sila prityazheniya, sozdavaemaya im v tochke
imeet
men'shuyu massu, i sila prityazheniya, sozdavaemaya im v tochke ![]() ,
,
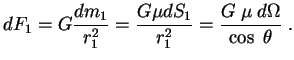
Teper' raspolozhim nashu probnuyu chasticu vne sfery (ris. 3). Sila, deistvuyushaya na chasticu v etom sluchae, ravna
i napravlena k centru sfery. Zdes'
Rassmotrim zvezdu radiusa ![]() c peremennoi plotnost'yu
c peremennoi plotnost'yu ![]() i polnoi massoi
i polnoi massoi
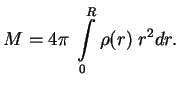
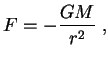
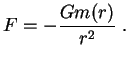
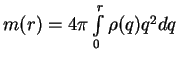 obychno nazyvayut tekushei massoi.
Velichina
obychno nazyvayut tekushei massoi.
Velichina
Reshenie nestacionarnyh zadach szhatiya zvezd, kak i lyubyh gidrodinamicheskih zadach,
mozhno provodit' dvumya sposobami. Vybiraya v kachestve nezavisimyh peremennyh
koordinatu ![]() i vremya
i vremya ![]() , mozhno rassmatrivat' izmeneniya fizicheskih velichin
(plotnosti, davleniya i t.d.) v kakoi-libo fiksirovannoi tochke prostranstva
(eilerov podhod). No chasto byvaet udobno sledit' za povedeniem vybrannyh zaranee
chastic veshestva (lagranzhev podhod), v etom sluchae nezavisimymi peremennymi
yavlyayutsya nachal'nye koordinaty
, mozhno rassmatrivat' izmeneniya fizicheskih velichin
(plotnosti, davleniya i t.d.) v kakoi-libo fiksirovannoi tochke prostranstva
(eilerov podhod). No chasto byvaet udobno sledit' za povedeniem vybrannyh zaranee
chastic veshestva (lagranzhev podhod), v etom sluchae nezavisimymi peremennymi
yavlyayutsya nachal'nye koordinaty ![]() i vremya
i vremya ![]() , a koordinata
, a koordinata ![]() yavlyaetsya funkciei
yavlyaetsya funkciei ![]() . Lagranzhev podhod chashe vsego osushestvlyaetsya v zadachah,
obladayushih kakoi-libo simmetriei dvizhenii, naprimer, pri sfericheski-simmetrichnom
rasshirenii (ili szhatii) zvezdy. Zadadim v nachal'nyi moment v kachestve lagranzhevoi
koordinaty rasstoyanie do centra zvezdy
. Lagranzhev podhod chashe vsego osushestvlyaetsya v zadachah,
obladayushih kakoi-libo simmetriei dvizhenii, naprimer, pri sfericheski-simmetrichnom
rasshirenii (ili szhatii) zvezdy. Zadadim v nachal'nyi moment v kachestve lagranzhevoi
koordinaty rasstoyanie do centra zvezdy ![]() . Sfera s radiusom
. Sfera s radiusom ![]() soderzhit
vpolne opredelennuyu chast' massy zvezdy
soderzhit
vpolne opredelennuyu chast' massy zvezdy ![]() , velichina kotoroi pri sfericheskih
dvizheniyah ne menyaetsya so vremenem. V etom sluchae tekushaya massa
, velichina kotoroi pri sfericheskih
dvizheniyah ne menyaetsya so vremenem. V etom sluchae tekushaya massa ![]() mozhet byt'
vybrana v kachestve nezavisimoi (lagranzhevoi) koordinaty.
mozhet byt'
vybrana v kachestve nezavisimoi (lagranzhevoi) koordinaty.
Rassmotrim neskol'ko primerov:
1. Shar radiusa ![]() imeet postoyannuyu plotnost'
imeet postoyannuyu plotnost' ![]() const. Ochevidno, chto reshenie
uravneniya (1.1) imeet vid
const. Ochevidno, chto reshenie
uravneniya (1.1) imeet vid
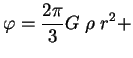 const
const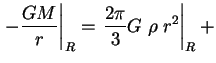 const
const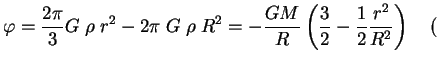 pri
pri2. Teper' predpolozhim, chto
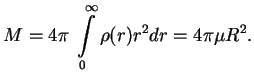
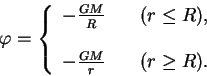
My vidim, chto v etom sluchae
![]() imeet razryv
(ris. 6). Mozhno pokazat',
chto etot rezul'tat sovershenno obshii: konechnaya massa, sosredotochennaya v beskonechno
tonkom sloe s konechnoi poverhnost'yu, daet razryv normal'noi proizvodnoi potenciala:
imeet razryv
(ris. 6). Mozhno pokazat',
chto etot rezul'tat sovershenno obshii: konechnaya massa, sosredotochennaya v beskonechno
tonkom sloe s konechnoi poverhnost'yu, daet razryv normal'noi proizvodnoi potenciala:
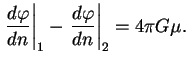
3. Dano:
![]() . Chemu ravno
. Chemu ravno
![]() ? Neposredstvennoe vychislenie
proizvodnyh daet nul' vezde, za isklyucheniem tochki
? Neposredstvennoe vychislenie
proizvodnyh daet nul' vezde, za isklyucheniem tochki ![]() . V samom dele
. V samom dele
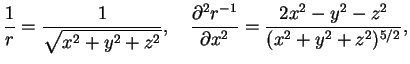
Eshe proshe v dannom sluchae vychislenie v sfericheskih koordinatah. Dlya potenciala, ne
zavisyashego ot ugla
![]() , i podstavlyaya
, i podstavlyaya
![]() , snova poluchim
, snova poluchim
![]() . Odnako nepravil'no bylo by otvechat', chto vezde
. Odnako nepravil'no bylo by otvechat', chto vezde
![]() .
Takoi otvet ne veren, tak kak potok
.
Takoi otvet ne veren, tak kak potok
![]() cherez lyubuyu poverhnost', okruzhayushuyu
nachalo koordinat, otlichen ot nulya i raven
cherez lyubuyu poverhnost', okruzhayushuyu
nachalo koordinat, otlichen ot nulya i raven ![]() . Pravil'nyi otvet:
. Pravil'nyi otvet:
4. Rassmotrim teper' obshii sluchai sfericheski-simmetrichnogo raspredeleniya plotnosti
![]() . Opredelim, kak ran'she, tekushuyu massu
. Opredelim, kak ran'she, tekushuyu massu
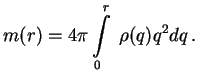
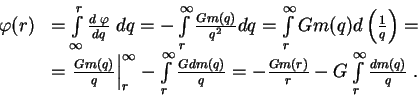
C uchetom sootnosheniya dlya ![]() zapishem vyrazhenie dlya potenciala v vide
zapishem vyrazhenie dlya potenciala v vide
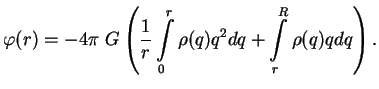
<< 1.2 Vektornoe pole uskorenii ... | Oglavlenie | 1.4 Energiya gravitacionnogo vzaimodeistviya >>
|
Publikacii s klyuchevymi slovami:
Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |