Astronet > 9.4 Obshie svoistva ravnovesiya relyativistskih zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 9.3 Sfericheski-simmetrichnoe pole ... | Oglavlenie | 9.5 Ustoichivost' relyativistskih ... >>

9.4 Obshie svoistva ravnovesiya relyativistskih zvezd

Rassmotrim nekotorye obshie svoistva etih reshenii dlya ravnovesnyh relyativistskih zvezd. Mehanicheskoe ravnovesie sootvetstvuet minimumu energii (t. e. massy) -- v obshem sluchae ekstremumu pri dannom kolichestve barionov i dannom raspredelenii entropii po barionam. V chastnom sluchae holodnogo veshestva entropiya vezde ravna nulyu. Reshenie, ustoichivoe otnositel'no radial'nyh peremeshenii, pri etom vsegda bezrazlichno otnositel'no konvekcii.

1. Pust' dano nekotoroe raspredelenie entropii . V sfericheski-simmetrichnom sluchae yavlyaetsya funkciei tekushego chisla barionov:

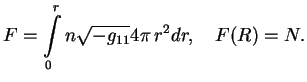
$\displaystyle F=\int\limits^r_0 n\sqrt{-g_{11}}4\pi \,r^2dr,\quad F(R)=N.$

-- lagranzheva koordinata, poetomu pri vseh variaciyah , v otlichie ot , vsegda fiksirovana. Sostoyanie ravnovesiya sootvetstvuet minimumu pri dannom pri variaciyah (ili ). (Vopros o konvektivnoi ustoichivosti zdes' ne stavitsya.)

2. Pust' zvezda izentropichna: const. Mozhno i v etom sluchae deistvovat' po-prezhnemu, t. e. nahodit' minimum pri variaciyah i fiksirovannom , no teper' proyavlyaetsya eshe odna stepen' svobody: my mozhem perestavlyat' chasticy mezhdu lyubymi sloyami. Pri perestanovke energiya ne dolzhna menyat'sya (v pervom poryadke). Otsyuda srazu poluchaetsya uslovie na himicheskii potencial veshestva $\mu$ :

$\displaystyle \mu e^{\nu/2}=$ const

(9.7)

po zvezde. Himpotencial opredelyaetsya kak prirashenie energii sistemy pri dobavlenii edinicy massy pokoya:

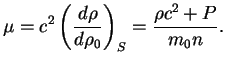
$\displaystyle \mu=c^2\left({d\rho\over{d\rho_0}}\right)_S={\rho c^2+P\over{m_0 n}}.$

Takoi vid vyrazheniya dlya $\mu$ ob'yasnyaetsya tem, chto esli vnutr' zvezdy pomestit' element massy $\Delta m_0$ , to rabota $\Delta m\sim \Delta m_0\rho/\rho_0\;+\;$ (rabota po razdviganiyu okruzhayushego veshestva) $\;\sim\Delta m_0P/\rho_0\,$ . Mnozhitel' $e^{\nu/2}$ igraet rol' gravitacionnogo potenciala (rabota po pereneseniyu barionov iz beskonechnosti ravna $\Delta\,M_0 e^{\nu(R)/2}$ ). Konstantu v (9.7) legko naiti iz uslovii na poverhnosti. Tam $P=0,\,\rho=0,\,\mu=c^2,$

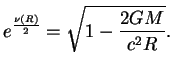
$\displaystyle e^{{\nu(R)\over2}}=\sqrt{1-{2GM\over{c^2R}}}.$

Itak,

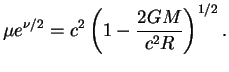
$\displaystyle \mu e^{\nu/2}=c^2\left(1-{2GM\over{c^2R}}\right)^{1/2}.$

Ris. 58.

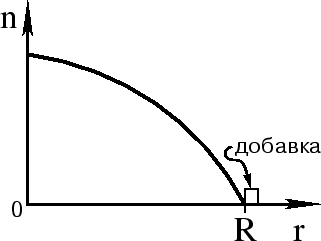
Predpolozhim, chto my hotim podschitat', kak izmenitsya massa zvezdy pri izmenenii chisla barionov, t. e. pri izmenenii . Dlya etogo nam nuzhno sravnit' dva blizkih, no raznyh resheniya. Eti dva resheniya razlichayutsya vo vseh tochkah. No iz principa ekstremuma yasno, chto mozhno snachala dobavit' bariony na poverhnosti (sm. ris. 58). Pri etom, vo-pervyh, izmenitsya massa

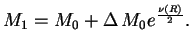
$\displaystyle M_1=M_0+\Delta\,M_0 e^{{\nu(R)\over2}}.$

Vo-vtoryh, eto reshenie ne ravnovesno. Poetomu zvezda perestroitsya. No izmenenie massy pri perestroike okolo ravnovesiya imeet vysshii poryadok malosti, poetomu v pervom poryadke massa i posle perestroiki ta zhe (sm. razdely 1.7, 1.8). V rezul'tate imeem

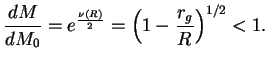
$\displaystyle {dM\over{dM_0}}=e^{{\nu(R)\over2}}=\left(1-{r_g\over R}\right)^{1/2}<1.$


Ris. 59.	Ris. 60.

Sledovatel'no,

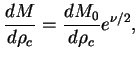
$\displaystyle {dM\over{d\rho_c}}={dM_0\over{d\rho_c}}e^{\nu/2},$

t. e. ekstremumy krivyh $M(\rho_c)$ i $M_0(\rho_c)$ sovpadayut (ris. 59). Interesno, chto pri nekotoroi $\rho_c$ velichina

stanovitsya bol'she

. Kak eto mozhet poluchitsya, esli

vsegda men'she edinicy? Vse ob'yasnyaetsya prosto: krivaya

ne gladkaya (ris. 60), poetomu ona mozhet peresech' bissektrisu

<< 9.3 Sfericheski-simmetrichnoe pole ... | Oglavlenie | 9.5 Ustoichivost' relyativistskih ... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce