Astronet > 9.5 Ustoichivost' relyativistskih zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 9.4 Obshie svoistva ravnovesiya ... | Oglavlenie | 9.6 Nesfericheskie polya ... >>

9.5 Ustoichivost' relyativistskih zvezd

Tochno takzhe, kak i v sluchae belyh karlikov, mozhno pokazat', chto pervyi maksimum na krivoi $M(\rho_c)$ sootvetstvuet ustoichivosti (sm. razdel; 7.2). Odnako poyavlenie minimuma $M(\rho_c)$ zdes' uzhe ne oznachaet vozvrata k ustoichivomu sostoyaniyu. Okazyvaetsya, chto v -om ekstremume krivoi $M(\rho_c)$ teryaet ustoichivost' -ya sobstvennaya moda radial'nyh kolebanii.

Ustoichivymi okazyvayutsya tol'ko zvezdy s $\rho_c<\rho_{c\;\max}$ . Odnako oni ustoichivy tol'ko otnositel'no malyh vozmushenii. Seichas my dokazhem, chto otnositel'no dostatochno bol'shih vozmushenii neustoichivo lyuboe ravnovesie (teorema Zel'dovicha).

Kogda my govorim, chto pri nekotorom $\rho_{c0}$ ravnovesie zvezdy ustoichivo, to eto znachit, chto lyubye neravnovesnye konfiguracii s tem zhe chislom barionov (t. e. s tem zhe ) imeyut v okrestnosti nashego resheniya $M(\rho_c)>M(\rho_{c0})$ . Pokazhem, chto pri bol'shih $\rho_c$ est' konfiguracii s ochen' maloi massoi: $M\ll M(\rho_{c0})$ (pri toi zhe ), t. e. otnositel'no bol'shih vozmushenii vsegda est' neustoichivost'.

Napishem vyrazhenie dlya massy zvezdy, kotoroe, kak my uzhe govorili, verno i dlya neravnovesnyh konfiguracii:

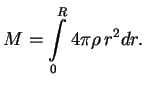
$\displaystyle M=\int\limits^R_0 4\pi\rho\,r^2dr.$

Chislo barionov

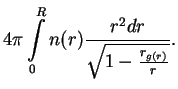
$\displaystyle 4\pi\int\limits^R_0 n(r){r^2dr\over{\sqrt{1-{r_{g(r)}\over r}}}}.$

Schitaem, chto dlya barionov spravedlivo uravnenie sostoyaniya ul'trarelyativistskogo gaza:

$\displaystyle \rho\sim n^{4/3}.$

Pust'

$\displaystyle \rho=A/r^2,\,$ sledovatel'no $\displaystyle ,\,r_g(r)/r=8\pi AG/c^2.$

Teper' poluchim, chto

$\displaystyle M=$ const $\displaystyle \cdot N^{3/2}A^{1/2}(1-8\pi AG/c^2).$

Vidno, chto vsegda mozhno vybrat'

tak, chto

skol' ugodno malo: $M\longrightarrow0$ pri $\rho_c\longrightarrow\infty$ . No yasno, chto pri konechnyh $\rho_c$ dolzhny byt' tochki s malym

, chto i dokazyvaet neustoichivost' lyubogo sostoyaniya.

Ocenim velichinu bar'era, kotoryi nado preodolet', chtoby zvezda poteryala ustoichivost'. Budem rabotat' v sisteme edinic $\hbar=c=1\,(G\ne 1)$ . V etih edinicah razmernost' dliny sovpadaet s razmernost'yu obratnoi massy:

$\displaystyle [px]=[h]=[mcx],\qquad [x]=[h/mc]=[1/m].$

$\displaystyle [$ Energiya $\displaystyle ]=[E]=[mc^2]=[m]=[1/x],\,[Gm^2]=[e^2]=[Ex]=[x^0],$

t. e.

v etih edinicah bezrazmerno.

V ul'trarelyativistskom gaze energiya chasticy $E=cp_F=n^{1/3}$ , sledovatel'no, energiya zvezdy (massa)

$\displaystyle M=EN=Nn^{1/3},$

a radius

$\displaystyle R\sim (N/n)^{1/3}.$

Teper' my hotim, chtoby radius konfiguracii, sostoyashei iz dannogo chisla barionov, ravnyalsya gravitacionnomu radiusu zvezdy

$\displaystyle r_g=GM=GN(n)^{1/3}=N^{1/3}n^{-1/3}=R,$

t. e.

$\displaystyle n=N^{-1}G^{-3/2}.$

Chtoby szhat' veshestvo do takoi plotnosti, nado zatratit' energiyu

$\displaystyle \Delta\,M=N^{2/3}G^{-1/2}-Nm.$

Otsyuda vidno, chto pri $N=N_{\mbox{krit}}(Gm^2)^{-3/2}$ bar'era voobshe net. Eto kriticheskoe chislo barionov sootvetstvuet maksimal'noi ravnovesnoi masse, tak kak ona mozhet skollapsirovat' bez bar'era (sm. razdel 2.4). Dlya malyh $N<N_{\mbox{krit}}$ otnositel'naya velichina bar'era rastet:

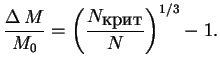
$\displaystyle {\Delta\,M\over{M_0}}=\left({N_{\mbox{krit}}\over N}\right)^{1/3}-1.$

Primer Zemli: $M_{\oplus}=3\cdot10^{-6}\,M_\odot$ . Dlya togo, chtoby pereiti bar'er, neobhodimo zatratit' energiyu okolo 100 $\,M_{\oplus}c^2$ .

Odnako v deistvitel'nosti eta ocenka bar'era ne imeet smysla. My opredelili velichinu bar'era iz soobrazhenii podobiya, t. e. schitali, chto zvezda szhimaetsya gomologicheski. A eto vovse ne obyazatel'no. Ekonomnee szhat' v centre maluyu chast' i zastavit' ee skollapsirovat'. Potom na obrazovavshuyusya chernuyu dyru upadet vse veshestvo. Berya vse men'shee kolichestvo veshestva, neobhodimo zatrachivat' vse men'shee kolichestvo energii, chtoby zastavit' ego skollapsirovat'.

Hotya dlya malyh mass energiya mala, etot rezul'tat nel'zya naiti metodom malyh vozmushenii, tak kak $\delta E/E$ stanovitsya vse bol'she i bol'she. Eshe raz povtorim, chto plotnost', do kotoroi nado szhat' veshestvo, s umen'sheniem massy vozrastaet (sm. razdel 7.1):

$\displaystyle \rho=2\cdot10^{16}\,(M_\odot/M)^2\,[$ g/sm $\displaystyle ^3].$

Takim obrazom, v klassicheskoi OTO bar'er svoditsya k nulyu. Odnako, kak obychno schitayut, kvantovye effekty stanovyatsya vazhnymi pri $r_g<10^{-33}$ sm, t. e. $m\sim 10^{-5}$ g. Zdes' bar'er $\sim mc^2=10^{16}\,$ erg

Dzh (eto ne tak malo). Odnako trudnost' zdes' ne v energii, a v tom, chtoby sozdat' stol' malyi radius. Nado razlichat' yavleniya neobhodimye (t. e. neizbezhnye) i vozmozhnye, po krainei mere, v principe. Kollaps holodnogo veshestva s massoi $M>2\,M_\odot$ neobhodim, t. e. massivnye zvezdy dolzhny kollapsirovat' posle ischerpaniya yadernogo goryuchego. Mozhno somnevat'sya, skol'ko ih v nashei Galaktike:

ili

. No v principe oni dolzhny sushestvovat'.

Te malomassivnye chernye dyry, o kotoryh my vyshe govorili, ne obyazatel'no sushestvuyut, tak kak oni ne poluchayutsya v rezul'tate evolyucii zvezd. Odnako oni mogut v principe obrazovat'sya na samyh rannih stadiyah rasshireniya Vselennoi iz pervichnogo veshestva i privodit' k interesnym kosmologicheskim sledstviyam. Kak pokazal Hoking, takie chernye dyry za schet kvantovyh processov ispuskayut teplovoe izluchenie s effektivnoi dlinoi volny . Pri etom chernaya dyra, teryaya massu, ``isparyaetsya''.

Dlya chernyh dyr zvezdnogo proishozhdeniya $M\sim M_\odot$ effekt ispareniya nichtozhen, uvelichenie massy v rezul'tate processov akkrecii okruzhayushego gaza gorazdo sil'nee. Dlya malyh chernyh dyr, v osobennosti pervichnyh, effekt velik, voznikaet mnozhestvo interesnyh voprosov, kotorye odnako, lezhat za predelami dannoi knigi.

<< 9.4 Obshie svoistva ravnovesiya ... | Oglavlenie | 9.6 Nesfericheskie polya ... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce