Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu
Fizicheskie osnovy stroeniya i evolyucii zvezd
<< 9.5 Ustoichivost' relyativistskih zvezd | Oglavlenie |

9.6 Nesfericheskie polya tyagoteniya

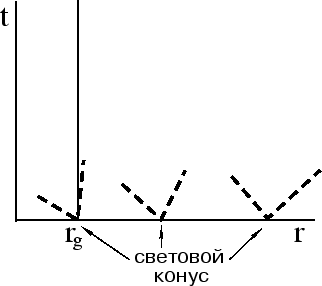
Naibolee harakternoe svoistvo polya Shvarcshil'da -- to, chto na nekotorom rasstoyanii ($ r<r_g$) nevozmozhen pokoi chastic. Sfera Shvarcshil'da kasatel'na svetovomu konusu (sm. ris. 61), poetomu nikakie chasticy (v tom chisle i ul'trarelyativistskie) ne mogut vyiti iz-pod radiusa $ r_g$, t. e. sferu Shvarcshil'da mozhno peresech' tol'ko snaruzhi vnutr'. Reshenie Shvarcshil'da otnositsya k sluchayu sfericheski-simmetrichnogo raspredeleniya veshestva. My znaem, chto ideal'nyh sfericheski-simmetrichnyh ob'ektov ne sushestvuet. Poetomu voznikaet estestvennyi vopros -- naskol'ko svoistva etogo resheniya ustoichivy otnositel'no vozmushenii sfericheskoi simmetrii?

Ustoichivost' shvarcshil'dovskoi singulyarnosti otnositel'no malyh vozmushenii metriki issledovali Redzhe i Uiler. Oni prishli k vyvodu, chto dlya stacionarnyh vozmushenii est' polya tol'ko dvuh tipov -- s osobennost'yu ili na poverhnosti Shvarcshil'da ili na beskonechnosti. Srazu voznikaet podozrenie, chto poverhnost' Shvarcshil'da mozhet byt' neustoichiva.

Ris. 61.

Metodom Redzhe-Uilera mozhno issledovat' ustoichivost' tol'ko otnositel'no malyh vozmushenii. Drugoi put' (pozvolyayushii issledovat' bol'shie vozmusheniya) -- eto poluchenie tochnyh reshenii uravnenii OTO, v kotoryh snyato trebovanie sfericheskoi simmetrii. Staticheskie resheniya dlya osesimmetrichnogo raspredeleniya mass ochen' davno poluchil Veil'. V etom reshenii istochnik polya (t. e. nekotoroe telo) predpolagaetsya ogranichennym. Poetomu na beskonechnosti metrika dolzhna perehodit' v evklidovu. Reshenie Veilya v chastnom sluchae sovpadaet s resheniem Shvarcshil'da (strogo govorya, ego mozhno perevesti v reshenie Shvarcshil'da nekotorym preobrazovaniem koordinat).

A v obshem sluchae sushestvuet kvadrupol'nyi moment gravitacionnogo polya. V etom reshenii poverhnost' $ g_{00}=0$ obladaet sovsem drugimi svoistvami, chem sfera Shvarcshil'da (gde $ g_{00}=1-r_g/r=0$ pri $ r=r_g$). V chastnosti, na poverhnosti $ g_{00}=0$ est' istinnaya osobennost' prostranstva-vremeni. V metrike Shvarcshil'da invariant

$\displaystyle C=R_{iklm}R^{iklm}=12/r_g^2$   pri$\displaystyle \,r=r_g, $

t. e. istinnoi osobennosti net (hotya $ g_{11}=(1-r_g/r)^{-1}\longrightarrow\infty$, odnako v deistvitel'nosti prostranstvo gladko -- est' sistemy otscheta, gde vse $ g_{ik}$ -- gladkie do centra; eto znachit prosto, chto metrika Shvarcshil'da v obychnoi zapisi ne goditsya dlya opisaniya prostranstva pri $ r<r_g$). V reshenii Veilya $ C$ imeet osobennost' na poverhnosti $ g_{00}=0$:

$\displaystyle C=A\,q^2\,g_{00}^{-1}+12/r_g^4+...\;, $

gde $ q$ -- kvadrupol'nyi moment. Krome togo, v otlichie ot polya Shvarcshil'da, svet dostigaet etoi poverhnosti za konechnoe vremya. Eto otrazhaet svoistva, naidennye Redzhe i Uilerom: te vozmusheniya, kotorye konechny na beskonechnosti, imeyut osobennost' na poverhnosti $ g_{00}=0$.

Eti vyvody ne yavlyayutsya svoistvom special'no kvadrupol'nogo otkloneniya ot sfericheskoi simmetrii. Mozhno pokazat', chto oni yavlyayutsya obshimi dlya lyubogo staticheskogo aksial'no-simmetrichnogo resheniya.

Mogut li real'nye tela sozdat' pole Veilya vo vsei oblasti $ g_{00}>0$? Kak uzhe govorilos', na beskonechnosti, v evklidovoi oblasti, pole Veilya sootvetstvuet gravitacionnomu polyu staticheskogo tela s neravnym nulyu kvadrupol'nym momentom. Odnako staticheskoe telo ne mozhet dat' takoe pole vplot' do poverhnosti $ g_{00}=0$ uzhe potomu, chto togda obrashaetsya v beskonechnost' gravitacionnaya sila. Eto bylo verno i v pole Shvarcshil'da, no my znaem, chto ego mozhno realizovat' nestaticheskimi telami, dvizhushimisya sfericheski-simmetrichnym obrazom (kollapsar).

Nel'zya li realizovat' reshenie Veilya nestaticheskimi telami? Okazyvaetsya i eto nevozmozhno. Mozhno pokazat', chto pri kollapse v soputstvuyushei sisteme otscheta moment perehoda granice tela poverhnosti $ g_{00}=0$ nichem ne vydelen: v etot moment na poverhnosti tela net istinnyh osobennostei prostranstva-vremeni ( $ C\ne\infty$), a v reshenii Veilya oni est'. Itak, poyavlenie istinnoi osobennosti v etom reshenii oznachaet, chto takoe raspredelenie mass realizovano byt' ne mozhet. Eto svyazano s tem, chto uravneniya polya odnovremenno yavlyayutsya uravneniyami dvizheniya.

Sovershenno tak zhe mozhno ubeditsya, chto rassmotrenie staticheski malyh vozmushenii resheniya Shvarcshil'da, provedennoe Redzhe i Uilerom, govorit ne o neustoichivosti etogo resheniya, a o fizicheskoi nevozmozhnosti realizovat' takie vozmusheniya. Tochnee govorya, staticheskie vozmusheniya polya Shvarcshil'da mozhno poluchit', tol'ko pomestiv sferu Shvarcshil'da vo vneshnee vozmushayushee pole. V reshenii Redzhe-Uilera eto sootvetstvuet vozmusheniyam konechnym na $ r_g$ i rashodyashimsya na beskonechnosti.

Imeyutsya osesimmetrichnye resheniya uravnenii OTO v vakuume ($ R_{ik}=0$) i drugogo tipa -- eto reshenie Kerra. Privedem metriku Kerra v vide, dannom Boeirom i Lindkvistom:

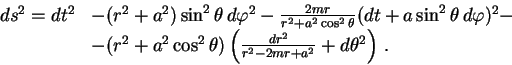\begin{displaymath}\begin{array}{ll} ds^2=dt^2&-(r^2+a^2)\sin^2\theta\,d\varphi^... ...eft({dr^2\over{r^2-2mr+a^2}}+d\theta^2\right)\,.\cr \end{array}\end{displaymath} (9.8)

My zapisali vyrazhenie dlya $ ds^2$ v takih edinicah, chto $ c=1,\,G=1$. Smysl simvolov $ m$ i $ a$, kak vsegda, nahodim issledovaniem predel'nyh sluchaev. Srazu vidno, chto pri $ a\longrightarrow0$ metrika Kerra perehodit v reshenie Shvarcshil'da, t. e. $ m$ mozhno interpretirovat' kak massu tela (v nashih edinicah $ r_g=2m$). Smysl simvola $ a$ vyyasnyaetsya pri perehode k beskonechnosti $ r\longrightarrow\infty$. Ochevidno, togda

$\displaystyle g_{00}=-g_{11}^{-1}=1-r_g/r, $

tak zhe kak dlya polya Shvarcshil'da. No est' i odno sushestvennoe otlichie:

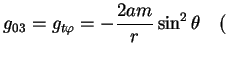$\displaystyle g_{03}=g_{t\varphi}=-{2am\over r}\sin^2\theta\quad($pri$\displaystyle r\longrightarrow\infty), $

t. e. nediagonal'naya komponenta metriki $ g_{03}$ otlichna ot nulya. V OTO pokazyvayut (sm., naprimer, ``Teoriyu polya'' Landau i Lifshica), chto v slabom pole (t. e. pri $ r\longrightarrow\infty$) u vrashayushegosya tela s momentom vrasheniya $ K$ poyavlyaetsya komponenta $ g_{03}$ imenno takogo vida:

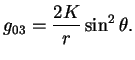
$\displaystyle g_{03}={2K\over r}\sin^2\theta. $

Eto pozvolyaet schitat', chto metrika Kerra opisyvaet vneshnee pole tela, vrashayushegosya s momentom

$\displaystyle K=-am. $

Pri poluchenii vyrazheniya dlya $ g_{03}$ v sluchae $ r\longrightarrow\infty$ my po sushestvu veli razlozhenie po stepenyam $ a/r$, poetomu eto vyrazhenie ostaetsya spravedlivym i v sil'nom pole vplot' do $ r\longrightarrow r_g$, esli $ a\longrightarrow0$. Metrika, zapisannaya v vide (), imeet smysl tol'ko pri $ 0\le a\le m$, t. e. $ a=m$ sootvetstvuet maksimal'no vozmozhnomu momentu central'nogo tela (t. e. $ K_{\rm {max}}=m^2$ ili v obychnyh edinicah $ K_{\rm {max}}=Mcr_g/2=GM^2/c$).

Esli podschitat' skalyar krivizny $ C$, to okazhetsya, chto metrika imeet osobennost' tol'ko pri $ r=0$. eto natalkivaet na mysl', chto metrika Kerra v otlichie ot metriki Veilya mozhet byt' realizovana real'nymi telami.

Rassmotrim, vo chto perehodit poverhnost' Shvarcshil'da v metrike Kerra. V shvarcshil'dovskom sluchae sfera $ r=r_g$ obladala dvumya glavnymi svoistvami: na nei $ g_{00}=0$ i, krome togo, ee kasalsya svetovoi konus. Iz-za vtorogo svoistva sfera Shvarcshil'da yavlyalas' kak by ``klapanom'': nikakie chasticy ne mogli peresech' ee iznutri naruzhu. Etot klapan, t. e. poverhnost', kasatel'nuyu svetovomu konusu, nazyvayut ``gorizontom sobytii''. V metrike Kerra okazyvaetsya, chto poverhnost' $ g_{00}=0$ i gorizont sobytii ne sovpadayut. Mozhno naiti, chto poverhnost' $ g_{00}=0$ opredelyaetsya vyrazheniem

$\displaystyle r_{\mbox{sh}}=m+\sqrt{m^2-a^2\cos^2\theta}\,, $

a gorizont sobytii

$\displaystyle r_{\mbox{gor}}=m+\sqrt{m^2-a^2}\,. $

Ochevidno, chto $ r_{\mbox{sh}}\ge r_{\mbox{gor}}$. Tak zhe kak v pole Shvarcshil'da uslovie $ g_{00}\ge 0$ ogranichivaet oblast', gde mozhno pokoitsya. Odnako v metrike Shvarcshil'da $ r_{\mbox{sh}}=r_{\mbox{gor}}$. Poetomu chasticy s $ r<r_{\mbox{sh}}$ mogli dvigat'sya tol'ko k centru. Teper' chasticy s $ r<r_{\mbox{sh}}$, no $ r>r_{\mbox{gor}}$ mogut dvigat'sya po radiusu v lyubuyu storonu, v chastnosti, mozhet byt' $ r=$const (hotya dlya nih nevozmozhno $ \varphi =$const, oni obyazany dvigat'sya po $ \varphi$ v tu zhe storonu, chto vrashaetsya telo). Oblast' $ r_{\mbox{gor}}\le r \le r_{\mbox{sh}}$ nazyvayut ergosferoi.

Kak budet menyat'sya metrika v prisutstvii svobodno padayushih chastic? Chasticy, kotorye dvizhutsya navstrechu vrasheniyu tela, zahvatyvayutsya ran'she. Poetomu, esli na central'noe telo padayut chasticy, imeyushie izotropnoe raspredelenie po skorostyam na beskonechnosti, to metrika Kerra teryaet moment i perehodit v metriku Shvarcshil'da, a oblako chastic priobretaet moment (tak kak chasticy zahvatyvayutsya vyborochno).

Privedem vyrazhenie dlya pricel'nogo parametra gravitacionnogo zahvata chasticy, dvizhusheisya v ekvatorial'noi ploskosti:

        a) pri $ v_{\infty}\ll c$:

$\displaystyle l={c\over{v_{\infty}}}\left[1+\left(1\pm{\vert a\vert\over m}\right)^{1/2}\right]r_{\mbox{sh}} $

(vybor znaka zavisit ot napravleniya momenta chasticy otnositel'no momenta central'nogo tela). Pri $ a=0,\,l=(2c/v_{\infty})r_g$:         b) pri $ v_{\infty}=c$ (zdes' tozhe vazhen znak momenta chasticy):

$\displaystyle l_+=4\cos^3\left[{1\over 3}(\pi-\arccos\vert a/m\vert)\right]r_{\mbox{sh}}, $

$\displaystyle l_-=4\cos^3\left[{1\over 3}\arccos\vert a/m\vert\right]r_{\mbox{sh}}. $

Ris. 62.

Zavisimost' parametrov zahvata v metrike Kerra ot znaka momenta interesno proyavlyaetsya v sluchae diskovoi akkrecii. Torn pokazal, chto pri $ a\ll m$ svet, izluchaemyi veshestvom pri akkrecii, pogloshaetsya chernoi dyroi tak, chto $ a\longrightarrow m$. Odnako, esli $ a$ pochti ravno $ m$, to moment otbiraetsya. Ustoichivoe znachenie $ a=0,948\,m$.

Penrouz pokazal, chto est' vozmozhnost' izvlekat' energiyu iz polya Kerra. Brosim chasticu tak, chtoby ona v ergosfere ( $ r_{\mbox{gor}}\le r \le r_{\mbox{sh}}$) raspadalas' na dve chasticy. Pust' odna iz novyh chastic uidet pod gorizont, a vtoraya vyletit iz-pod $ r_{\mbox{sh}}$ (ris. 62). Mozhno osushestvit' etot process tak, chto vernuvshayasya chastica prineset energii bol'she, chem otpravlennaya. Yasno, chto pri etom umen'shaetsya energiya central'nogo tela.

Voznikaet zadacha: skol'ko energii mozhno otnyat' u chernoi dyry? Hoking pokazal, chto est' nekotoraya invariantnaya massa, kotoruyu processami takogo roda nel'zya umen'shit'. V metrike Shvarcshil'da ploshad' sfery $ r=r_g$ ravna

$\displaystyle S=4\pi r_g^2=16\pi m^2. $

V metrike Kerra mozhno podschitat' ploshad' gorizonta sobytii:

\begin{displaymath} \begin{array}{ll} S=\int &\sqrt{g_{22}g_{33}}\,d\theta\,d\va... ...a^2)^{1/2})^2+a^2]=8\pi m[m+(m^2-a^2)^{1/2}]\,. \cr \end{array}\end{displaymath}

Teorema Hokinga sostoit v tom, chto $ S$ ne mozhet umen'shat'sya. Eto pozvolyaet opredelit' invariantnuyu massu chernoi dyry

$\displaystyle S\equiv 16\pi m^2_{\rm inv}\,. $

Podobnye issledovaniya pokazali, chto pri ochen' obshih predpolozheniyah edinstvennym tochnym osesimmetrichnym resheniem s otsutstviem singulyarnosti na gorizonte sobytii yavlyaetsya reshenie Kerra. Mozhno pokazat', chto pri kollapse pod $ r_{\mbox{gor}}$ lyubogo vrashayushegosya tela metrika Kerra voznikaet kak predel'naya pri $ t\longrightarrow\infty$ dlya vsei oblasti vne $ r_{\mbox{gor}}$. Vse eto pozvolyaet schitat', chto metrika Kerra opisyvaet pole lyuboi vrashayusheisya chernoi dyry. Otmetim, chto real'naya chernaya dyra dolzhna imet' moment vrasheniya $ a$ skoree blizhe k $ a=m$, chem k $ a=0$. V razmernyh edinicah $ a=m$ sootvetstvuet momentu $ K=GM^2/c$. Dlya $ M=1\,M_\odot$ eto daet znachenie poryadka momenta vrasheniya Solnca. No Solnce -- eto ochen' medlenno vrashayushayasya zvezda. U massivnyh zvezd udel'nyi moment vrasheniya mozhet byt' na dva poryadka bol'she.


<< 9.5 Ustoichivost' relyativistskih zvezd | Oglavlenie |

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu
Ocenka: 3.0 [golosov: 120]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya