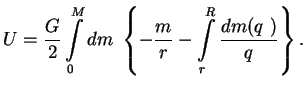Astronet > 1.4 Energiya gravitacionnogo vzaimodeistviya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 1.3 Sfericheski-simmetrichnye polya tyag... | Oglavlenie | 1.5 Davlenie gaza ... >>

1.4 Energiya gravitacionnogo vzaimodeistviya

My videli, chto energiya gravitacionnogo vzaimodeistviya dlya dvuh mass i ravna $U=-{Gm_1m_2\over r}$ . Na sluchai tochechnyh mass vyrazhenie dlya obobshaetsya sleduyushim obrazom:

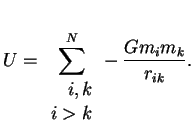
$\displaystyle U=\sum_{\begin{array}{rcl}i,k\\ i>k\\ \end{array}}^N -\,{Gm_im_k\over r_{ik}}.$

Pri takom opredelenii

kazhdaya para $m_i,\;m_k$ vhodit v summu tol'ko odin raz. Vvedem velichinu

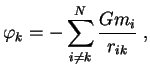
$\displaystyle \varphi_k=-\sum_{i\ne k}^N {Gm_i\over r_{ik}}\;,$

chto, ochevidno, predstavlyaet soboi gravitacionnyi potencial, sozdavaemyi v

-toi tochke vsemi ostal'nymi massami. Teper' dlya

mozhno napisat'

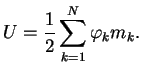
$\displaystyle U={1\over 2}\sum_{k=1}^N \varphi_km_k.$

Koefficient ${1\over 2}$ poyavilsya vsledstvie togo, chto kazhdaya para tochek vhodit v summu dva raza. Eto vyrazhenie legko obobshit' na sluchai nepreryvnoi sredy:

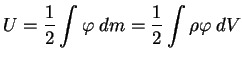
$\displaystyle U={1\over 2}\int \varphi \;dm={1\over 2}\int \rho \varphi\;dV$

(po opredeleniyu $dm=\rho \;dV$ ).

Dlya tochechnyh mass neobhodimo bylo otbrasyvat' energiyu samodeistviya, ogovarivaya pravilo summirovaniya. V sploshnoi srede samodeistvie ne uchityvaetsya avtomaticheski. Po poryadku velichiny $dV \sim \;{(dr)}^3$ , i samodeistvie elementa est' $G{(\rho dV)}^2/dr \sim {(dr)}^5$ , t.e. velichina bolee vysokogo poryadka, chem energiya vzaimodeistviya s ostal'nymi massami, kotoraya $\sim {(dr)}^3$ .

Ispol'zuem teper' vyrazhenie $\varphi$ dlya sfericheski-simmetrichnogo raspredeleniya $\rho (r)$ i vychislim gravitacionnuyu energiyu. Imeem:

$\displaystyle U={G\over 2}\int\limits_0^M dm \;\left\{-{m\over r}-\int\limits_r^R {dm (q\ )\over q}\right\}.$

(1.3)

Eto vyrazhenie mozhno znachitel'no uprostit'. Vvedem vspomogatel'nuyu funkciyu 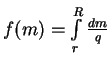$f(m)=\int\limits_r^R {dm\over q}$ . Ochevidno,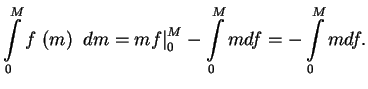

i krome etogo

$\displaystyle \int\limits_0^M f \;(m) \; \left. dm=mf \right\vert _0^M -\int\limits_0^M mdf=-\int\limits_0^M mdf.$

Imeem takzhe

Takim obrazom, integral ot pervogo chlena v vyrazhenii (1.3) raven integralu ot vtorogo, i okonchatel'no poluchim

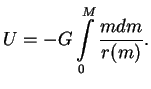
$\displaystyle U=-G\int\limits_0^M{mdm\over r(m)}.$

Eto vyrazhenie proshe poluchit' inym putem, rassmatrivaya, kakuyu rabotu sovershayut gravitacionnye sily pri narashivanii dannoi konfiguracii posledovatel'nymi sloyami. Pust' massa

s radiusom

uzhe izgotovlena. Pribavim k etoi masse novyi sfericheskii sloi

. Togda sovershennaya rabota, ochevidno, ravna $dU= {Gmdm\over r}$ i t.d. V rezul'tate poluchim

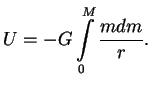
$\displaystyle U=-G\int\limits_0^M {mdm\over r}.$

<< 1.3 Sfericheski-simmetrichnye polya tyag... | Oglavlenie | 1.5 Davlenie gaza ... >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce