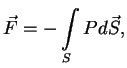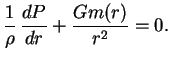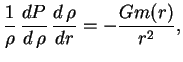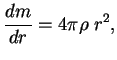<< 1.4 Energiya gravitacionnogo vzaim... | Oglavlenie | 1.6 Osnovy termodinamiki zvezd >>
1.5 Davlenie gaza. Uravnenie ravnovesiya
zvezdy
Dlya zvezdy, nahodyasheisya v ravnovesii, sila gravitacionnogo prityazheniya,
deistvuyushaya na kakoi-libo element massy ![]() , dolzhna byt' skompensirovana
ravnoi po velichine i protivopolozhnoi po napravleniyu siloi. Takaya uravnoveshivayushaya
gravitaciyu sila v zvezdah obuslovlena davleniem veshestva (tochnee, gradientom
davleniya).
, dolzhna byt' skompensirovana
ravnoi po velichine i protivopolozhnoi po napravleniyu siloi. Takaya uravnoveshivayushaya
gravitaciyu sila v zvezdah obuslovlena davleniem veshestva (tochnee, gradientom
davleniya).
V obshem sluchae davlenie ![]() yavlyaetsya velichinoi, pozvolyayushei opisat' silu,
deistvuyushuyu na vydelennyi v zhidkosti ili gaze ob'em
yavlyaetsya velichinoi, pozvolyayushei opisat' silu,
deistvuyushuyu na vydelennyi v zhidkosti ili gaze ob'em ![]() proizvol'noi formy
so storony okruzhayushego ego veshestva, kak integral po razdelyayushei poverhnosti
proizvol'noi formy
so storony okruzhayushego ego veshestva, kak integral po razdelyayushei poverhnosti
gde davlenie
Dlya zhidkosti, v kotoroi davlenie odnorodno (
![]() const), imeem ochevidnoe vyrazhenie
dlya sily, deistvuyushei na zamknutuyu poverhnost':
const), imeem ochevidnoe vyrazhenie
dlya sily, deistvuyushei na zamknutuyu poverhnost': ![]() . Pust' teper' davlenie
neodnorodno. V obshem sluchae v maloi okrestnosti nekotoroi tochki, raskladyvaya v
ryad, mozhno zapisat':
. Pust' teper' davlenie
neodnorodno. V obshem sluchae v maloi okrestnosti nekotoroi tochki, raskladyvaya v
ryad, mozhno zapisat':
Podstavlyaya (1.5) v (1.4), naidem, chto s tochnost'yu do velichin vtorogo poryadka malosti sila, deistvuyushaya na ob'em
V ravnovesii dlya nevrashayusheisya zvezdy eti dve sily dolzhny kompensirovat' drug druga, t.e.
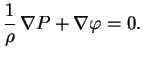
Dlya sfericheski-simmetrichnyh zvezd uravnenie gidrostaticheskogo ravnovesiya imeet vid
Sila gravitacionnogo prityazheniya napravlena k centru zvezdy. Uravnoveshivayushaya
sila davleniya proporcional'na
![]() , t.e. dlya podderzhaniya ravnovesiya
zvezdy davlenie dolzhno s neobhodimost'yu monotonno rasti ot poverhnosti k centru
zvezdy.
, t.e. dlya podderzhaniya ravnovesiya
zvezdy davlenie dolzhno s neobhodimost'yu monotonno rasti ot poverhnosti k centru
zvezdy.
Vydelim vnutri zvezdy edinichnyi cilindricheskii ob'em (
![]() sm
sm![]() sm
sm![]() sm
sm![]() ) tak, chtoby osnovaniya cilindra byli
perpendikulyarny radiusu. Dlya takogo ob'ema sila, obuslovlennaya davleniem, ravna
) tak, chtoby osnovaniya cilindra byli
perpendikulyarny radiusu. Dlya takogo ob'ema sila, obuslovlennaya davleniem, ravna
![]() din/sm
din/sm![]() . Vydelim teper' sharovoi sektor s rastvorom
telesnogo ugla
. Vydelim teper' sharovoi sektor s rastvorom
telesnogo ugla ![]() (sm. ris. 7).
Kazalos' by, poskol'ku sila davleniya na
vneshnyuyu poverhnost' sharovogo sektora ravna
(sm. ris. 7).
Kazalos' by, poskol'ku sila davleniya na
vneshnyuyu poverhnost' sharovogo sektora ravna
![]() , to rezul'tiruyushaya
sila davleniya, deistvuyushaya na edinichnyi ob'em etogo sektora, ravna
, to rezul'tiruyushaya
sila davleniya, deistvuyushaya na edinichnyi ob'em etogo sektora, ravna
![]() . Ne budet li bolee pravil'nym podstavlyat' eto
vyrazhenie v (1.6) vmesto velichiny
. Ne budet li bolee pravil'nym podstavlyat' eto
vyrazhenie v (1.6) vmesto velichiny
![]() ? Okazyvaetsya net. Pri
vyvode sily, deistvuyushei na sharovoi sektor, my ne uchli davlenie na bokovye
poverhnosti sektora, chto daet dobavochnuyu silu vdol' radiusa
? Okazyvaetsya net. Pri
vyvode sily, deistvuyushei na sharovoi sektor, my ne uchli davlenie na bokovye
poverhnosti sektora, chto daet dobavochnuyu silu vdol' radiusa
![]() . S uchetom poslednego my opyat' prihodim k vyrazheniyu dlya sily
gazovogo davleniya
. S uchetom poslednego my opyat' prihodim k vyrazheniyu dlya sily
gazovogo davleniya
![]() .
.
V obshem sluchae neizotropnogo davleniya sleduet primenyat' vyrazhenie
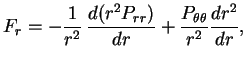
Predpolozhim, chto nam izvestno uravnenie sostoyaniya v vide
![]() , t.e.
davlenie yavlyaetsya funkciei tol'ko plotnosti. Zadadimsya znacheniyami v centre
, t.e.
davlenie yavlyaetsya funkciei tol'ko plotnosti. Zadadimsya znacheniyami v centre
![]() i
i
![]() . Togda imeem sistemu dvuh obyknovennyh differencial'nyh
uravnenii pervogo poryadka:
. Togda imeem sistemu dvuh obyknovennyh differencial'nyh
uravnenii pervogo poryadka:
reshaya kotoruyu, poluchaem raspredelenie plotnosti i davleniya vdol' radiusa.
Rassmotrim asimptoticheskoe povedenie resheniya v centre (![]() ) i na krayu
zvezdy (
) i na krayu
zvezdy (![]() ). Pri
). Pri ![]() poluchim
poluchim
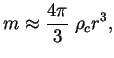
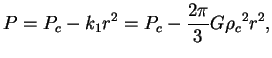
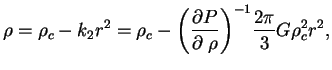
Na krayu zvezdy imeem ![]() i, integriruya uravnenie ravnovesiya (1.7),
poluchim
i, integriruya uravnenie ravnovesiya (1.7),
poluchim
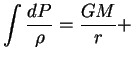 const
const
Esli davlenie yavlyaetsya stepennoi funkciei plotnosti
![]() , to
neobhodimym (no ne dostatochnym) usloviem konechnosti atmosfery yavlyaetsya
, to
neobhodimym (no ne dostatochnym) usloviem konechnosti atmosfery yavlyaetsya ![]() . V etom sluchae
. V etom sluchae
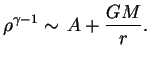
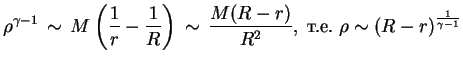
Pri opredelennom uravnenii sostoyaniya ![]() ne vsegda mozhno reshit' zadachu
dlya dannoi massy (mozhet okazat'sya, chto reshenii dlya vybrannoi massy voobshe ne
sushestvuet). Odnako, zadavayas' central'noi plotnost'yu
ne vsegda mozhno reshit' zadachu
dlya dannoi massy (mozhet okazat'sya, chto reshenii dlya vybrannoi massy voobshe ne
sushestvuet). Odnako, zadavayas' central'noi plotnost'yu ![]() , mozhno naiti
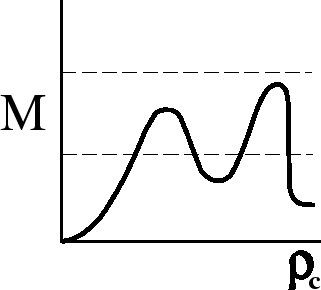
nabor reshenii s razlichnymi massami, t.e. postroit' krivuyu
, mozhno naiti
nabor reshenii s razlichnymi massami, t.e. postroit' krivuyu ![]() (ris. 8).
Posle etogo uzhe vidno, kakie resheniya sootvetstvuyut dannoi masse, pri kakih
massah sushestvuyut resheniya (t.e. sostoyaniya ravnovesiya) i t.p.
(ris. 8).
Posle etogo uzhe vidno, kakie resheniya sootvetstvuyut dannoi masse, pri kakih
massah sushestvuyut resheniya (t.e. sostoyaniya ravnovesiya) i t.p.
Takoi zhe podhod primenim i v OTO. Kachestvenno vse ostaetsya po-prezhnemu: reshenie mozhno nahodit', integriruya ot centra, tak kak vneshnie sloi ne sozdayut uskoreniya.
<< 1.4 Energiya gravitacionnogo vzaim... | Oglavlenie | 1.6 Osnovy termodinamiki zvezd >>
|
Publikacii s klyuchevymi slovami:
Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |