Astronet > 1.6 Osnovy termodinamiki zvezd

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Fizicheskie osnovy stroeniya i evolyucii zvezd

<< 1.5 Davlenie gaza... | Oglavlenie | 1.7 Variacionnyi princip >>

1.6 Osnovy termodinamiki zvezd

Ogranichimsya sluchaem himicheski odnorodnoi zvezdy. Odnoi iz samyh vazhnyh termodinamicheskih funkcii veshestva yavlyaetsya udel'naya teplovaya energiya . Pust' izvestna kak funkciya udel'nogo ob'ema $v={1/ \rho}\;[$ smg i udel'noi entropii .

Po I zakonu termodinamiki . Poetomu, znaya , mozhno naiti i drugie termodinamicheskie velichiny. Naprimer,

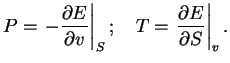
$\displaystyle P=\left.-{\partial E\over \partial v}\right\vert _S; \quad T=\left.{\partial E\over \partial S}\right\vert _v.$

Pri zadannoi temperature inogda pri raschetah udobno pol'zovat'sya svobodnoi energiei sistemy :

$\displaystyle dF=-Pdv-SdT.$

Takim obrazom, . Odnako pri issledovanii mehanicheskoi ustoichivosti ravnovesnoi zvezdy vazhno znat' , tak kak processy teploprovodnosti v zvezde ochen' medlennye i poetomu pul'sacii proishodyat adiabaticheski, t.e. s sohraneniem entropii, no ne temperatury.

Vvedem eshe odnu vazhnuyu termodinamicheskuyu funkciyu -- ental'piyu

$\displaystyle dH=TdS+vdP.$

$\begin{wrapfigure}{r}{0.5\textwidth} \epsfxsize =0.45\textwidth \hbox to0.5\textwidth{\hss\epsfbox{fig/f09.ai}\hss} \end{wrapfigure}$

Ris. 9.

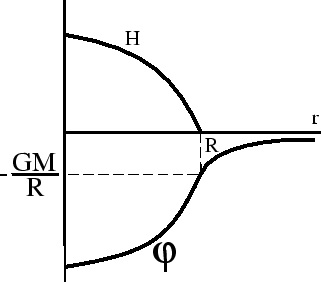
Esli entropiya fiksirovana, to $\left.dH\right\vert _S=vdP={dP\over \rho}$ . Ispol'zuya eto sootnoshenie, zapishem uslovie ravnovesiya zvezdy $-{1\over \rho} \,\nabla P- \,\nabla \varphi=0$ v vide $- \,\nabla {(H+\varphi)}=0$ . Itak, dlya izentropicheskih zvezd ( const) uslovie ravnovesiya est' $H+\varphi=$ const po zvezde. Na krayu $P=0, \;\rho=0, \;H=0,$ poetomu const $=-{GM\over R}$ . Vnutri zvezdy ental'piya yavlyaetsya ``zerkal'nym otrazheniem'' $\varphi$ (ris. 9).

Kakov fizicheskii smysl sootnosheniya $H+\varphi=$ const? Voz'mem 1 g holodnogo veshestva na beskonechnosti i pomestim ego v zvezdu na rasstoyanii ot centra. Rabota gravitacionnogo polya pri etom ravna $\varphi (r)$ . Chtoby etot gramm nahodilsya v ravnovesii s veshestvom zvezdy, ego neobhodimo nagret' do temperatury okruzhayushei sredy , pridat' ob'em , t.e. sovershit' rabotu . Krome etogo, neobhodimo proizvesti rabotu , osvobozhdaya polost' ob'ema , v kotoruyu my pomestim nash element. Itak, polnaya rabota ravna $\varphi+E+Pv= \varphi+H$ . Uslovie $\varphi+H=$ const govorit o tom, chto zatrachennaya rabota ne zavisit ot mesta, v kotorom my razmeshaem element veshestva.

Vmesto togo, chtoby brat' element veshestva na beskonechnosti, my mozhem vzyat' ego v drugom meste zvezdy. Togda uslovie $H+\varphi=0$ oznachaet, chto polnaya rabota pri perestanovke dvuh elementov ravna nulyu, t.e. izentropicheskaya zvezda nahoditsya v bezrazlichnom ravnovesii otnositel'no takih perestanovok.

<< 1.5 Davlenie gaza... | Oglavlenie | 1.7 Variacionnyi princip >>

Publikacii s klyuchevymi slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy Publikacii so slovami: Evolyuciya zvezd - vnutrennee stroenie zvezd - termoyadernye reakcii - fizicheskie processy
Sm. takzhe: Pererabotka veshestva v Kassiopee A NGC 7789: Roza Karoliny Planetarnaya tumannost' NGC 2818 ot Habbla Nauchnaya konferenciya "Nablyudaemye proyavleniya evolyucii zvezd" v SAO RAN Planetarnye tumannosti Proshlye i budushie zvezdy Andromedy Tumannost' Ozherel'e Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce