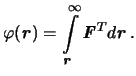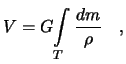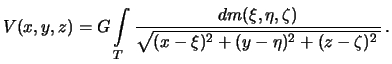<< 2.6 Zemletryaseniya | Oglavlenie | 3.2 Svoistva potenciala >>
3. Gravitacionnoe pole planety
Razdely
- 3.1 Gravitacionnyi potencial
- 3.2 Svoistva gravitacionnogo potenciala
- 3.3 Gravitacionnyi potencial shara
- 3.4 Gravitacionnoe pole planety
3.1 Gravitacionnyi potencial
Podrazdely
Potencialom nazyvaetsya rabota, kotoruyu nuzhno sovershit', kotoruyu nuzhno
sovershit', chtoby peremestit' dannuyu material'nuyu tochku s massoi, ravnoi
edinice, iz zadannoi tochki v beskonechnost'. Pust'
est'
vektor-sila, prilozhennaya k material'noi tochke,
-- radius-vektor
etoi tochki. Togda potencialom budet velichina
Vvedem ponyatie silovoi funkcii 
. Po opredeleniyu chastnaya proizvodnaya
silovoi funkcii vdol' lyubogo napravleniya 
ravna komponente sily vdol' etogo
napravleniya. Otsyuda sleduet, chto
.
Takim obrazom, podyntegral'noe vyrazhenie v formule (3.1) est' ne chto inoe, kak polnyi differencial silovoi funkcii, poetomu
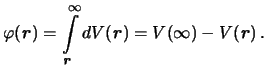
Silovuyu funkciyu na beskonechnosti mozhno priravnyat' nulyu, poetomu budem schitat', chto potencial i silovaya funkciya otlichayutsya lish' znakom.
V gravimetrii, kak razdele geofiziki, tradicionno ne razdelyayut eti dva ponyatiya, i pod terminom gravitacionnyi potencial obychno ponimayut silovuyu funkciyu. V nashem kurse my takzhe budem priderzhivat'sya etih tradicii.
3.1.1 Gravitacionnyi potencial material'noi tochki
Soglasno zakonu N'yutona, dve material'nye tochki prityagivayutsya drug k drugu s
siloi, pryamo proporcional'noi ih massam i obratno proporcional'no kvadratu
rasstoyaniya mezhdu nimi. Vyberem sistemu koordinat tak, chtoby odna iz
material'nyh tochek okazalas' v nachale etoi sistemy. Togda drugaya
material'naya tochka budet imet' radius-vektor
. Vektor
napryazhennosti gravitacionnogo polya v tochke s radius-vektorom
raven sile, kotoraya deistvuet na material'nuyu tochku s massoi, ravnoi
edinice. Vektor etoi sily mozhno izobrazit' sleduyushim obrazom
, gde 
-- gravitacionnaya postoyannaya. Proekcii
etoi sily na osi dekartovoi sistemy koordinat budut ravny
,
,
. Absolyutnaya velichina etogo
vektora, ravna
Zametim, chto razmernost' napryazhennosti polya tyagoteniya sovpadaet s razmernost'yu uskoreniya, poetomu chasto vmesto sily prityazheniya edinicy massy, ili udel'noi sily prityazheniya govoryat ob uskorenii sily prityazheniya, hotya, mozhet byt', v etom slovosochetanii mozhno usmotret' i smyslovuyu nelepicu.
Formulu (3.2) eshe nazyvayut kak zakon obratnyh kvadratov. Ves' opyt nebesnoi mehaniki govorit o tom, chto v masshtabah Solnechnoi sistemy on rabotaet ochen' horosho: ne naideno kakih libo podozrenii, chto ego nuzhno podpravlyat'. Laboratornye eksperimenty po opredeleniyu gravitacionnoi postoyannoi G dali povod podozrevat', chto etot zakon ne absolyutno strog. Hotya prichinoi nesootvetstviya teorii i praktiki vpolne mogli byt' i neizvestnye sistematicheskie pogreshnosti. V konce minuvshego veka nablyudalsya povyshennyi interes k zakonu obratnyh kvadratov. V raznyh stranah provodilis' eksperimenty i primenyalis' sovremennye samye vysokotochnye instrumenty dlya obnaruzheniya kakih-libo nevyazok mezhdu teoriei i praktikoi. Odnako, nikakih znachimyh rashozhdenii ne obnaruzheno.
Netrudno ubedit'sya, chto gravitacionnyi potencial tochki (silovaya funkciya)
raven,
, gde 
-- rasstoyanie mezhdu prityagivayushimisya
tochkami (skalyarnaya velichina).
3.1.2 Gravitacionnyi potencial tela
Strogo govorya, zakon obratnyh kvadratov rabotaet tol'ko dlya material'nyh tochek. Odnako, fiziki-teoretiki i eksperimentatory dokazyvayut, chto dlya gravitacionnogo polya vypolnyaetsya princip superpozicii: gravitacionnoe pole dvuh material'nyh tochek (ili tel) ravno summe gravitacionnyh polei kazhdoi iz etih tochek (ili tel) po otdel'nosti. Inache govorya, sily tyagoteniya ne ekraniruyutsya.
Soglasno principa superpozicii, gravitacionnyi potencial 
tochek raven summe
gravitacionnyh potencialov vseh tochek
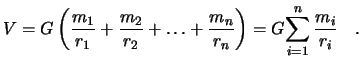
Esli tochek beskonechnoe chislo, a massy ih beskonechno maly, to imeem delo s integral'noi summoi, i nashu formulu sleduet zapisat' tak
gde 
-- rasstoyanie mezhdu fiksirovannoi tochkoi 
i elementom prityagivayushei massy
.
Pust' 
, 
, 
-- koordinaty tochki , a 
, 
, 
-- koordinaty tekushei tochki s massoi dm togda
formulu (3.3) mozhno perepisat' sleduyushim obrazom m
Privedennyi integral beretsya po vsemu ob'emu tela, eto trehkratnyi integral.
Ego velichina zavisit ot raspredeleniya plotnostei vnutri tela.
<< 2.6 Zemletryaseniya | Oglavlenie | 3.2 Svoistva potenciala >>
|
Publikacii s klyuchevymi slovami:
gravimetriya - geofizika - solnechnaya sistema - seismologiya
Publikacii so slovami: gravimetriya - geofizika - solnechnaya sistema - seismologiya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
