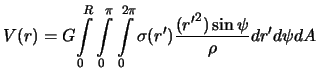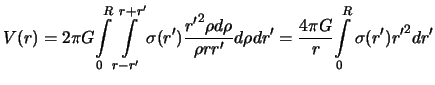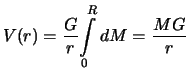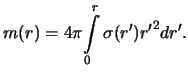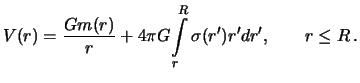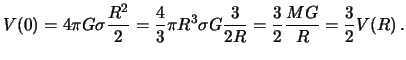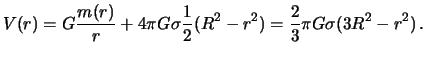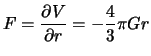po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu

Razdely

• 3.3.1 Potencial shara vo vnutrennei tochke
• 3.3.2 Gravitacionnyi potencial odnorodnogo shara

3.3 Gravitacionnyi potencial shara

Vse planety Solnechnoi sistemy imeyut sfericheskuyu formu. Poetomu imeet smysl opredelit' gravitacionnyi potencial shara. Dlya uprosheniya zadachi, my budem predpolagat', chto plotnost' shara zavisit tol'ko ot rasstoyaniya do ego centra Netrudno ubedit'sya, chto takoi shar prityagivaet tochno tak zhe, kak i material'naya tochka s massoi ravnoi masse shara i pomeshennaya v ego centr. Chtoby v etom ubedit'sya, neobhodimo dlya formuly (3.4) vybrat' takuyu sistemu koordinat, s pomosh'yu kotoroi bylo by udobno vypolnyat' integrirovanie.

Dlya nachala, predstavim sebe, chto tochka nahoditsya vne shara. Soedinim etu tochku s centrom shara (tochka O), poluchennyi radius-vektor oboznachim cherez . Radius-vektor elementa massy budem oboznachat' bukvoi . Sledovatel'no rasstoyanie mezhdu elementom massy i tochkoi , kotoroe my oboznachili grecheskoi bukvoi , budet imet' vid , gde -- ugol s vershinoi v centre shara, obrazovannyi radius-vektorami i . Nakonec, element massy opredelyaetsya proizvedeniem plotnosti na ob'em elementarno malogo parallelepipeda so storonami , , i . Zdes' my vveli eshe odnu stepen' svobody -- povorot vokrug osi na ugol . Takim obrazom,

Teper' vmesto formuly (3.4) zapisat'

(3.5)

Zamenim peremennuyu integrirovaniya na . Opredelim predely integrirovaniya. Ochevidno, chto vmesto 0 i nuzhno vzyat' i , a . Peremennuyu podyntegral'noe vyrazhenie ne soderzhit, poetomu vnutrennii integral legko beretsya. Vmesto (3.5) teper' budem imet'

(3.6)

Netrudno dogadat'sya, chto est' massa beskonechno tonkoi sfery , poetomu

(3.7)

Takim obrazom, my prishli k ochen' vazhnomu vyvodu: shar so sfericheski simmetrichno raspredelennoi massoi prityagivaet tak zhe, kak i material'naya tochka s massoi ravnoi masse shara i pomeshennoi v ego centre.

3.3.1 Potencial shara vo vnutrennei tochke

Rassmotrim snachala beskonechno tonkii sharovoi sloi s vnutrennei polost'yu, ne soderzhashei massy. Togda mozhno dokazat', chto vnutri etoi polosti potencial (silovaya funkciya) est' postoyannaya velichina, to est' etot sharovoi sloi vnutrennyuyu tochku ne prityagivaet. Obratimsya k risunku. Cherez tochku provedem konicheskuyu poverhnost' s vershinoi v etoi tochke. Togda eta poverhnost' vyrezhet na sfericheskoi poverhnosti elementarnuyu ploshadku , a na drugoi storone sfery -- elementarnuyu ploshadku . Tochka lezhit pod ploshadkoi na rasstoyanii i ispytyvaet so storony etoi ploshadki prityazhenie, ravnoe , gde -- koefficient proporcional'nosti, zavisyashii ot poverhnostnoi plotnosti etogo shara i ot napravleniya vneshnei normali k ploshadke po otnosheniyu k radiusu-vektoru tochki . Elementarnaya ploshadka raspolozhena na rasstoyanii ot tochki . Poskol'ku obe ploshadki vidny iz tochki pod odnim i tem zhe telesnym uglom, to

Itak, obe sily ravny i napravleny v protivopolozhnye storony. Teper' budem rassuzhdat' sleduyushim obrazom. Cherez tochku R provedem ploskost' perpendikulyarnuyu radius-vektoru etoi tochki. Ona razdelit sfericheskii "puzyr'" na dve chasti, nazovem ih uslovno verhnyuyu i nizhnyuyu. Poskol'ku kazhduyu iz chastei mozhno predstavit' kak beskonechnuyu summu elementarnyh ploshadok, to dlya kazhdoi elementarnoi ploshadki verhnei polusfery naidetsya simmetrichnaya ei ploshadka v nizhnei polusfere. Sily prityazheniya material'noi tochki, pomeshennoi v tochku , so storony verhnei i nizhnei polusfer ravny i protivopolozhny po napravleniyu. Otsyuda vyvod: material'naya tochka, pomeshennaya vnutri poloi sfery, etoi sferoi ne prityagivaetsya

Rassuzhdeniya, privedennye zdes', nel'zya schitat' strogo matematicheski obosnovannymi. My rasschityvaem bol'she na intuiciyu, chem na stroguyu matematicheskuyu logiku. Odnako, v teorii potenciala prityazheniya matematicheski strogo dokazano, chto obolochka ne prityagivaet material'nuyu tochku i v sluchae, kogda eta obolochka imeet ellipsoidal'nuyu formu.

My pokazali, chto gravitacionnyi potencial v polosti, okruzhennoi sfericheskoi poverhnost'yu, yavlyaetsya postoyannoi velichinoi. Odnako, eto imeet mesto lish' v tom sluchae, kogda eta polost' prityagivayushih mass ne soderzhit. Teper' otkazhemsya ot etogo usloviya, i budem schitat', chto shar ne polyi, no plotnost' zavisit tol'ko ot rasstoyaniya do centra shara. Provedem cherez tochku sferu tak, chto ona razdelit shar na vnutrennii shar s massoi i sharovoi sloi s massoi . Material'naya tochka budet prityagivat'sya tol'ko vnutrennim sharom, tak kak sharovoi sloi, kak my videli, vnutrennyuyu tochku ne prityagivaet. Poetomu gravitacionnaya sila v tochke napravlena v centr shara i ravna .

Znak "minus" my postavili, chtoby podcherknut', chto sila napravlena v storonu, protivopolozhnuyu radius-vektoru. Massu vnutrennego shara mozhno poluchit', integriruya massu beskonechno tonkoi sfery v predelah ot 0 do

(3.8)

Poskol'ku , to dlya gravitacionnogo potenciala vo vnutrennei tochke shara poluchim

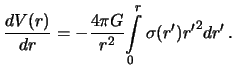
Integriruya, budem imet'

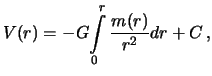
gde S -- postoyannaya integrirovaniya. Poluchennoe vyrazhenie mozhno prointegrirovat' po chastyam. . Soglasno formule (3.8) : , poetomu 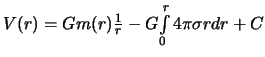. Opredelim teper' postoyannuyu . My znaem, chto , poetomu 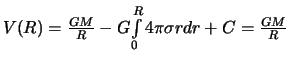. Sledovatel'no .

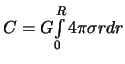Okonchatel'no, formula dlya gravitacionnogo potenciala vo vnutrennei tochke shara so sfericheski simmetrichnoi raspredelennoi massoi prinimaet vid

(3.9)

Pri perehode cherez poverhnost' potencial sohranyaet nepreryvnost'. Ochevidno, chto pri , budem imet' -- potencial tochki s massoi, ravnoi , raspolozhennoi v centre shara. V sluchae, kogda tochka nahoditsya v centre shara, to est' pri , , a 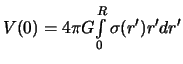, to eta velichina zavisit ot zakona izmeneniya plotnosti s glubinoi. V chastnosti, esli shar -- odnorodnyi, to ego potencial v centre shara raven

(3.10)

Otsyuda sleduet vyvod, chto gravitacionnyi potencial v centre odnorodnogo shara v poltora raza bol'she, chem na ego poverhnosti.

3.3.2 Gravitacionnyi potencial odnorodnogo shara

Gravitacionnyi potencial odnorodnogo shara vo vneshnei tochke nichem ne otlichaetsya ot potenciala shara, so sfericheski simmetrichnym raspredeleniem massy, poetomu my etot sluchai rassmatrivat' ne budem. Gravitacionnyi potencial odnorodnogo shara vo vnutrennei tochke mozhet byt' vychislen po formule (3.9), v kotoroi nuzhno polozhit' plotnost' postoyannoi velichine. Imeem

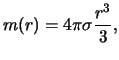
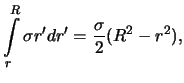
sledovatel'no

(3.11)

V centre shara ()      -- znachenie, sovpadayushee s privedennym znacheniem v formule (3.10). Na ego poverhnosti .

Opredelim silu prityazheniya vo vnutrennei tochke:

(3.12)

Takim obrazom: sila prityazheniya vnutrennei material'noi tochki so storony mass sfericheskogo tela lineino rastet po absolyutnoi velichine s rasstoyaniem ot centra shara i napravlena k ego centru. Drugimi slovami, zakon N'yutona, ili, kak eshe ego nazyvayut, zakon obratnyh kvadratov, prevrashaetsya v zakon Guka -- zakon pryamoi proporcional'nosti "uprugoi" sily ot velichiny otkloneniya tela ot polozheniya ravnovesiya.

Nuzhno otmetit', chto esli ravnomerno raspredelennaya prityagivayushaya massa zanimaet ob'em, ogranichennyi ellipsoidal'noi poverhnost'yu, to i v etom sluchae vmesto zakona N'yutona sleduet brat' zakon Guka.

Pokazhem teper', chto vo vnutrennei tochke gravitacionnyi potencial podchinyaetsya zakonu Puassona: , gde -- plotnost' veshestva v tochke .

Budem schitat', chto my imeem delo s proizvol'nym telom, ogranichennym zamknutoi poverhnost'yu . Vydelim vnutri nego fiksirovannuyu tochku i okruzhim ee sferoi s ochen' malen'kim radiusom, s tem, chtoby plotnost' maloi sfery schitat' postoyannoi velichinoi. Pust' -- potencial vseh mass tela v tochke za isklyucheniem maloi sfery, -- potencial maloi sfery, togda . Potencial udovletvoryaet uravneniyu Laplasa, tak kak tochka yavlyaetsya vneshnei po otnosheniyu k rassmatrivaemoi oblasti, a dlya potenciala vo vnutrennei tochke odnorodnogo malogo shara my poluchili

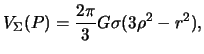
gde -- radius maloi sfery. Opredelim operator Laplasa dlya gravitacionnogo potenciala v tochke . Uchityvaya skazannoe vyshe, budem imet'

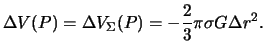
Poskol'ku , to , sledovatel'no , a eto i est' uravnenie Puassona.

Pri perehode tochki cherez poverhnost', gde plotnost' izmenyaetsya skachkom, izmenitsya skachkoobrazno i pravaya chast' uravneniya Puassona, levaya chast' kotorogo predstavlyaet soboi summu vtoryh proizvodnyh. Otsyuda sleduet i razryv nepreryvnosti vtoryh proizvodnyh gravitacionnogo potenciala.

Versiya dlya pechati