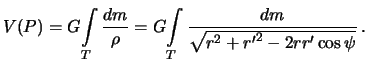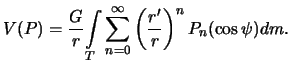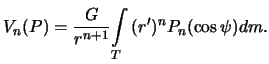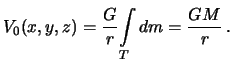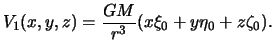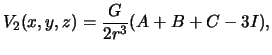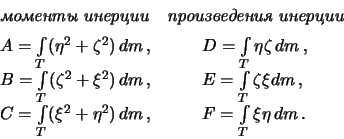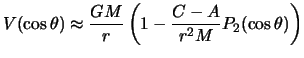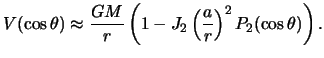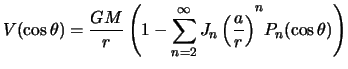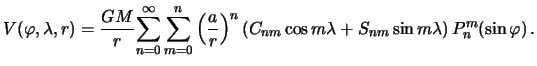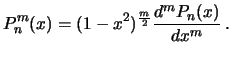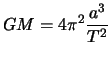<< 3.3 Gravitacionnyi potencial shara | Oglavlenie | 4. Gravitacionnoe pole i ... >>
3.4 Gravitacionnoe pole planety
Vse planety Solnechnoi sistemy imeyut formu, blizkuyu k sfericheskoi. Poetomu, gravitacionnoe pole shara mozhno rassmatrivat', kak pervoe priblizhenie k gravitacionnomu polyu planety. Vo vtorom priblizhenii mozhno uchest' tot fakt, chto nekotorye planety, v tom chisle i Zemlya, gorazdo luchshe mogut byt' predstavleny ellipsoidom vrasheniya, chem sharom. V tret'em priblizhenii my mozhem uchest' i nekotorye osobennosti v raspredelenii mass vnutri planety i t.d. Koroche govorya, gravitacionnoe pole planety obychno predstavlyayut ryadom po sharovym funkciyam. V zavisimosti ot reshaemoi zadachi, pred'yavlyayutsya raznye trebovaniya k detal'nosti ishodnyh dannyh, k chislu chlenov razlozheniya i k chislu ishodnyh parametrov.
Itak, budem schitat', chto nasha fiksirovannaya tochka 
, v kotoroi nam neobhodimo
poluchit' gravitacionnyi potencial planety, -- vneshnyaya. Snova, kak i v
privedennyh vyshe formulah, budem schitat', chto vektor
opredelyaet koordinaty fiksirovannoi tochki , a absolyutnaya velichina etogo
vektora -- rasstoyanie tochki ot nachala koordinat. Radius-vektor elementa
massy 
my snova budem oboznachat' bukvoi
.
Rasstoyanie mezhdu fiksirovannoi tochkoi i elementom massy --
bukvoi 
.
Integrirovanie po ob'emu tela planety my budem pomechat' nizhnim predelom 
.
Zapishem gravitacionnyi potencial planety v vide integrala
Poskol'ku tochka lezhit vne planety i, kak pravilo, dostatochno daleko ot nee
udalena, to podyntegral'noe vyrazhenie mozhno razlozhit' v ryad po stepenyam
otnosheniya 
. My tut zhe stolknemsya s tak nazyvaemymi polinomami Lezhandra, na nekotoryh
svedeniyah o ih svoistvah neobhodimo ostanovit'sya.
Funkciei, proizvodyashei polinomy Lezhandra, nazyvaetsya funkciya
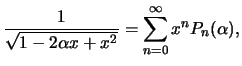
gde
-- polinomy Lezhandra stepeni 
. Vot neskol'ko pervyh
polinomov Lezhandra:
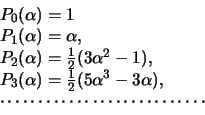
Kazhdyi sleduyushii polinom mozhno vychislit', pol'zuyas' rekurrentnoi formuloi
Sushestvuet i obshaya formula dlya polinomov Lezhandra. Eto tak nazyvaemaya
formula Rodriga
Vernemsya snova k nashemu integralu (3.13). Vynesem iz pod kornya velichinu 
,
poluchim
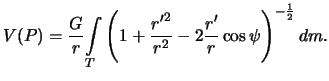
Pod znak integrala teper' vhodit proizvodyashaya funkciya polinomov Lezhandra.
Razlagaya podyntegral'noe vyrazhenie v stepennoi ryad otnositel'no otnosheniya
, budem imet'
Predstavim poluchennoe razlozhenie v vide
gde
Poluchennyi ryad nazyvayut ryadom Laplasa, a sootvetstvuyushie funkcii
-- funkciyami Laplasa. Ispol'zuetsya i drugaya terminologiya. Funkcii Laplasa mogut byt'
opredeleny cherez garmonicheskie (udovletvoryayushie uravneniyu Laplasa) odnorodny
polinomy, kotorye nosyat nazvanie sharovyh funkcii. Poetomu ryad (3.14) posle vypolneniya
ukazannogo integrirovaniya, nazyvayut razlozheniem gravitacionnogo potenciala v ryad po sharovym funkciyam.
Opredelim pervye tri funkcii Laplasa. Chtoby vypolnit' integrirovanie, nam
nuzhno vybrat' sistemy koordinat. Dopustim, chto tochka 
-- nachalo dekartovoi
sistemy koordinat. Napravleniya osei, v principe, ne imeyut znacheniya.
Koordinaty fiksirovannoi tochki my budem oboznachat' cherez 
, a dlya elementa
massy -- koordinaty 
, 
, 
.
Takim obrazom vektor
,
a radius-vektor elementa massy est'
.
Pervyi chlen razlozheniya.
Soglasno formule (3.15), imeem
Poluchennaya sharovaya funkciya daet lish' massu planety. Esli ogranichivat'sya tol'ko pervym chlenom razlozheniya, to eto ravnosil'no tomu, chto planeta otozhdestvlyaetsya s sharom so sfericheski simmetrichno raspredelennymi massami ili s material'noi tochkoi.
Vtoroi chlen razlozheniya
Sleduyushaya sharovaya funkciya imeet vid
.
Poskol'ku
, budem imet'
.
Podyntegral'noe vyrazhenie est' ne chto inoe, kak skalyarnoe proizvedenie dvuh
vektorov
i
:
,
poetomu
V astronomicheskih prilozheniyah etot chlen razlozheniya chasto ne prinimayut vo vnimanie: predpolagayut, chto nachalo sistemy koordinat vybrano tochno v centre mass. Odnako, bolee detal'nyi analiz gravitacionnyh polei planet inogda privodit k vyvodu o smeshenii centra mass po otnoshenii k geometricheskomu centru ob'ema planety.
Tretii chlen razlozheniya
Dlya 
poluchim
.
Zametim, chto
. Poetomu
Posle neobhodimyh preobrazovanii, poluchennuyu formulu mozhno privesti k vidu
gde ispol'zovany sleduyushie oboznacheniya:
a 
-- moment inercii planety otnositel'no osi, provedennoi cherez nachalo
koordinat i tochku . Opredelim napravlyayushie kosinusy tochki :
,
,
.
Kak sleduet iz teoreticheskoi mehaniki,
Takim obrazom, sharovaya funkciya nulevoi stepeni est' massa planety (moment inercii nulevogo poryadka), pervoi stepeni opredelyaetsya cherez koordinaty centra mass (moment inercii pervogo poryadka) sharovaya funkciya vtoroi stepeni opredelyaetsya cherez momenty inercii vtorogo poryadka. Prodolzhaya rassuzhdeniya, my ubedimsya v tom, s uvelicheniem stepeni sharovoi funkcii, uvelichivaetsya i poryadok momentov inercii planety, cherez kotorye eti sharovye funkcii opredelyayutsya. Poetomu govoryat, chto chleny razlozheniya gravitacionnogo potenciala vysokogo poryadka opredelyayutsya cherez mul'tipol'nye momenty ee massy.
V zadachah nebesnoi mehaniki chasto ispol'zuyutsya sleduyushie uprosheniya predstavleniya gravitacionnogo potenciala, v predpolozhenii, chto
- -- nachalo koordinat sovpadaet s centrom mass,
- -- napravleniya osei parallel'ny glavnym osyam inercii,
- -- figura planety -- telo vrasheniya.
Pri etih predpolozheniyah koordinaty centra mass i proizvedeniya inercii ravny
nulyu, a 
. Vyberem dekartovu sistemu koordinat sleduyushim obrazom:
os' Oz sovpadaet
s os'yu vrasheniya figury, a osi Ox i Oy
lezhat v ekvatorial'noi ploskosti. Togda
Odnako,
, poetomu
.
Podstavlyaya eto vyrazhenie v formulu dlya sharovoi funkcii vtoroi stepeni,
poluchim
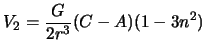
Kak my videli, velichina ravna kosinusu ugla mezhdu os'yu vrasheniya planety i
napravleniem na tochku .
Oboznachim etot ugol grecheskoi bukvoi 
, takim
obrazom
,
. Po opredeleniyu polinomov Lezhandra, imeem
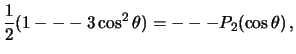
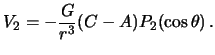
Esli ogranichit'sya tol'ko etimi chlenami razlozheniya, to gravitacionnyi potencial planety mozhno zapisat' v vide
Formula (3.21) pokazyvaet,
chto napryazhennost' gravitacionnogo polya v tochke
zavisit ne tol'ko ot sfericheskih koordinat etoi tochki: rasstoyaniya i
polyarnogo rasstoyaniya (ili shiroty) , no i ot otlichiya momentov inercii okolo
polyarnoi i ekvatorial'nyh osei. V kachestve fundamental'noi postoyannoi polya
planety berut ne raznost' 
, kotoraya zavisit ot massy i razmerov planety, a
bezrazmernuyu velichinu
. Teper' vmesto formuly (3.21)
mozhno zapisat'
Prinimaya vo vnimanie drugie chleny razlozheniya potenciala, no sohranyaya glavnoe uslovie -- vnutrennee stroenie planety sootvetstvuet telu vrasheniya -- my mozhem poluchit' formulu dlya gravitacionnogo potenciala, soderzhashuyu polinomy Lezhandra bolee vysokih stepenei
Koefficienty razlozheniya 
i 
otnosyatsya
k fundamental'nym postoyannym astronomii.
V kachestve harakteristiki planety ispol'zuyut takzhe bezrazmernyi moment inercii, kotoryi opredelyaetsya
sleduyushim obrazom
. Eta velichina malaya, esli pochti
vsya massa planety sosredotochena v ee centre, ona ravna 0.4, esli planeta --
odnorodnyi shar. Real'no 0.0 < 
< 0.4. Lyubopytno, chto amerikanskii
uchenyi Ekhard dlya Luny opredelil > 0.4, chto oznachaet Luna vnutri
pustaya! Bolee pozdnie opredeleniya bezrazmernogo momenta inercii Luny
ustanovili, chto on raven 0.391, chto ukazyvaet na ee odnorodnost', no
nikakih protivorechii s ustanovivshimisya vzglyadami na stroenie planet net. Eshe
odna fundamental'naya postoyannaya, takzhe svyazannaya s momentami inercii, --
postoyannaya precessii
igraet vazhnuyu rol' v teorii vrasheniya
planety.
V zaklyuchenii razdela privedem chislennye znacheniya fundamental'nyh postoyannyh dlya nekotoryh planet i Luny.
Real'no gravitacionnoe pole vo vneshnem prostranstve zavisit ne tol'ko ot
polyarnogo rasstoyaniya ili shiroty tochki , no i ot ee dolgoty -- ot ugla mezhdu
ploskost'yu meridiana, v kotoroi lezhit tochka , i ploskost'yu nulevogo
meridiana. Dlya Zemli -- eto grinvichskii meridian. Pust' 
-- shirota,
a 
--
dolgota tochki . Uchityvaya, chto
, v
privedennyh formulah funkciyu
, kotoraya vhodit v kachestve
argumenta dlya polinomov Lezhandra, my dolzhny zamenit' na
. Ne
ostanavlivayas' podrobno na vyvode formuly razlozheniya gravitacionnogo
potenciala v ryad po sharovym funkciyam, privedem gotovyi rezul'tat
Funkcii
i
nazyvayutsya sfericheskimi, tak kak znacheniya ih zavisyat tol'ko
ot polozheniya tochki na sfere (zadany shirota i dolgota). Parametry i 
sootvetstvenno nazyvayutsya stepen'yu i poryadkom otdel'noi sfericheskoi garmoniki. Funkciya
nazyvaetsya prisoedinennoi (associativnoi) funkciei Lezhandra. Ona opredelyaetsya cherez polinomy Lezhandra
sleduyushim obrazom
Obratim vnimanie na vnutrennyuyu summu v formule (3.24). Ee verhnii predel raven
, tak kak pri 
poryadok proizvodnoi v formule (3.25) budet bol'she stepeni polinoma i vse
sootvetstvuyushie chleny budut ravny nulyu.
Garmoniki nazyvayutsya zonal'nymi, esli ih znacheniya izmenyayutsya tol'ko s shirotoi. Eto
budet imet' mesto pri =0. Vnutri odnoi zony, otdelennoi ot drugih s severa i
s yuga parallelyami, zonal'naya garmonika sohranyaet svoi znak.
Garmoniki nazyvayutsya sektorial'nymi, esli ih znak mozhet izmenyat'sya tol'ko s dolgotoi. Eto
imeet mesto pri 
. Prisoedinennaya funkciya Lezhandra, pri etom, ravna
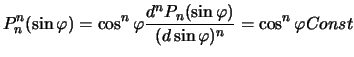
Poskol'ku kosinus shiroty ne menyaet znaka, to vnutri odnogo sektora ne izmenyaet znaka i sfericheskaya garmonika. Shar okazyvaetsya raschlenennym na sektora -- polosy, kotorye soedinyayut severnyi i yuzhnyi polyusa.
Garmoniki, dlya kotoryh 
na poverhnosti shara obrazuyut mozaichnuyu
kartinu, podobno shahmatnoi doske i nazyvayutsya tesseral'nymi ot latinskogo tessera-
mozaichnyi kubik. Sektorial'nye i tesseral'nye garmoniki pri vrashenii planety
sozdayut vo vneshnem prostranstve peremennoe vo vremeni gravitacionnoe pole,
chto znachitel'no oslozhnyayut teoriyu dvizheniya iskusstvennyh i estestvennyh
sputnikov planety.
3.4.1 Opredelenie massy planety
Pervyi chlen razlozheniya gravitacionnogo potenciala imeet vid 
. Esli by
drugie chleny razlozheniya ne okazyvali nikakogo deistviya na dvizhenie
sputnikov, ili, hotya by vozmusheniya ot nih byli za predelami tochnosti
nablyudeniya, dvizhenie sputnika podchinyalos' by zakonu Keplera.
Pust' 
-- massa planety, kotoruyu nuzhno opredelit', -- massa sputnika. Pod
deistviem sil prityazheniya, podchinyayushihsya zakonu obratnyh kvadratov, oba
nebesnyh tela dvizhutsya po ellipticheskim orbitam, v fokuse kazhdoi iz nih
raspolozhen centr mass sistemy (baricentr). V chastnom sluchae -- eto mogut byt'
i krugovye orbity. Dlya uprosheniya voprosa imenno etot sluchai my i budem
rassmatrivat'. Pust' 
-- rasstoyanie sputnika ot planety, 
-- rasstoyanie
sputnika ot baricentra, togda
. Dvigayas' po krugovoi orbite, sputnik
imeet uskorenie, ravnoe
, gde
, a -- period obrasheniya sputnika.
Otsyuda
Pri 
vyrazhenie v skobkah mozhno ne otlichat' ot
edinicy i formulu dlya opredeleniya massy planety perepisat' v sleduyushem vide
Poluchennaya formula est' ne chto inoe, kak tretii zakon Keplera: kvadraty periodov obrasheniya planet, otnosyatsya tak zhe, kak kuby ih rasstoyanii do central'nogo tela (Solnca).
Pravda, formulu (3.26) my poluchili dlya chastnogo sluchaya krugovogo dvizheniya,
hotya v nebesnoi mehanike dokazano, chto ona spravedliva i dlya ellipticheskogo
dvizheniya. V etom sluchae pod nuzhno ponimat' bol'shuyu poluos' ellipticheskoi
orbity.
Formula (3.26) daet vozmozhnost' opredelit' massu planety tol'ko v tom sluchae,
kogda gravitacionnaya postoyannaya nam izvestna. Ee opredelyayut s pomosh'yu
fizicheskogo eksperimenta. K sozhaleniyu, tochnost' etih eksperimentov poka eshe
ne dostatochno vysoka, hotya so vremeni Kavendisha -- angliiskogo uchenogo,
kotoryi odnim iz pervyh opredelil gravitacionnuyu postoyannuyu, tochnost' ee
opredeleniya vyrosla na dva poryadka za 150 let. Seichas prinyato
SI. Proizvedeniya gravitacionnoi
postoyannoi na massu opredelyayutsya znachitel'no tochnee. Naprimer, dlya Zemli eta
velichina ravna
, to est' otnositel'naya
pogreshnost' ravna 
, togda kak otnositel'naya pogreshnost'
gravitacionnoi postoyannoi sostavlyaet priblizitel'no 
. V kachestve
fundamental'nyh postoyannyh chasto rassmatrivayut imenno proizvedeniya mass na
gravitacionnuyu postoyannuyu, kotorye nazyvayut planetocentricheskimi gravitacionnymi postoyannymi (
geocentricheskaya, selenocentricheskaya, areocentricheskaya i t.d.)
3.4.2 Opredelenie harakteristik gravitacionnogo polya Zemli
Chem detal'nee nam nuzhno znat' gravitacionnoe pole, tem bol'shee chislo parametrov opredelyayut analiticheskoe vyrazhenie dlya silovoi funkcii polya tyagoteniya planety. V epohu, kogda sputniki eshe byli nedostupny, osnovnym metodom issledovaniya gravitacionnogo polya byl gravimetricheskii. Gravimetriya -- oblast' geofiziki, izuchayushaya sposoby naibolee vysokotochnogo opredeleniya udel'noi sily tyazhesti i ee geologicheskoi interpretacii. Etoi naukoi zanimayutsya kak fiziki, mehaniki tak i geologi.
Do 20-h godov HH stoletiya nauka ne raspolagala sredstvami dlya izmereniya
udel'noi sily tyazhesti na moryah i okeanah s tochnost'yu dostatochnoi, dlya ee
geologicheskogo istolkovaniya. V 1922-1929 gg gollandskii uchenyi-geodezist
Vening-Meines razrabotal sposob nablyudeniya kolebanii mayatnikov na slabo
kachayushemsya osnovanii. Ispol'zuya podvodnuyu lodku v kachestve laboratorii, on
sovershil ryad plavanii v Yugo-Vostochnuyu Aziyu, issledoval region, soderzhashii
ostrovnye dugi i glubokovodnye vpadiny. Idei Vening-Meinesa byli realizovany
v Gosudarstvennom astronomicheskom institute im. P.K. Shternberga professorom
L.V.Sorokinym. Do Velikoi Otechestvennoi voiny L.V,Sorokin s uchenikami
sovershil ryad plavanii na podvodnyh lodkah na Chernom more, v Barencovom,
Ohotskom i Beringovom moryah. Tol'ko voina ostanovila eti issledovaniya.
Odnako, posle voiny oni vnov' aktivizirovalis'. Byli razrabotany i drugie
metody dlya izmereniya sily tyazhesti na obychnyh issledovatel'skih sudah, byli
izobreteny morskie gravimetry, sposobnye izmeryat' prirashenie sily tyazhesti s
otnositel'noi tochnost'yu ne huzhe . V morskih gravimetricheskih
issledovaniyah posle voiny prinimali aktivnoe uchastie i drugie strany, v
chastnosti SShA, Angliya, Germaniya, Franciya, Italiya i Yaponiya. Oni i seichas
prodolzhayut aktivnoe issledovanie gravitacionnyh polei akvatorii, v
osobennosti neftegazonosnyh akvatorii.
Nakopilsya dostatochno bol'shoi material dlya opredeleniya modeli gravitacionnogo polya Zemli kak planety. Po mere nakopleniya novyh dannyh proizvodilas' reviziya etih modelei.
Odna iz poslednih modelei gravitacionnogo polya po geofizicheskim dannym byla postroena v GAISh professorom N.P. Grushinskim.
Nastoyashuyu revolyuciyu v opredelenii gravitacionnogo polya planety proizveli
pervye zapuski iskusstvennyh sputnikov Zemli. Byl otmechen rezkii skachek v
tochnosti opredeleniya postoyannoi -- postoyannoi, otvetstvennoi za
szhatie planety -- odnim iz osnovnyh parametrov, neobhodimyh dlya
razvertyvaniya kart na Zemnoi poverhnosti. Seichas razrabotany novye metody
nablyudeniya ISZ, kotorye pozvolyayut opredelit' polozhenie sputnika s tochnost'yu
2 sm. Vozniklo novoe napravlenie nebesnoi mehaniki, pozvolyayushee
po vidimym neravenstvam v dvizhenii sputnika opredelyat' vozmushayushie sily --
gravitacionnoe pole planety. Kak izvestno obratnye zadachi dinamiki otnosyatsya
k tipu nekorrektnyh, teoriyu kotoryh razrabotali uchenye MGU i uspeshno
ispol'zuyutsya dlya resheniya zadach kak geofiziki, tak i astrofiziki.
Seichas postroeno dostatochno mnogo modelei gravitacionnogo polya Zemli raznoi detal'nosti i tochnosti. Otmecheno, chto s uvelicheniem stepeni i poryadka razlozheniya padaet tochnost' opredeleniya koefficientov. Dlya opisaniya regional'nogo polya chasto pribegayut k modeli stepeni i poryadka 36 (36h36). Naibolee detal'naya iz izvestnyh modelei, po-vidimomu, model', poluchivshaya shifr EGM-96 (360h360).
<< 3.3 Gravitacionnyi potencial shara | Oglavlenie | 4. Gravitacionnoe pole i ... >>
|
Publikacii s klyuchevymi slovami:
gravimetriya - geofizika - solnechnaya sistema - seismologiya
Publikacii so slovami: gravimetriya - geofizika - solnechnaya sistema - seismologiya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
