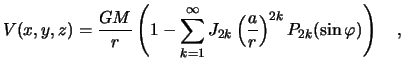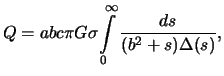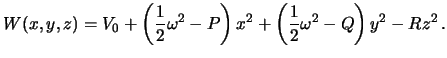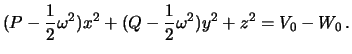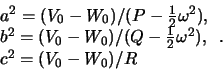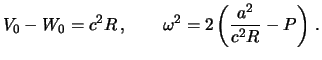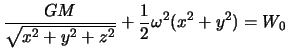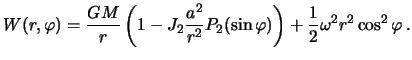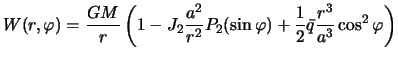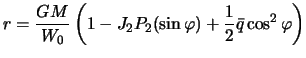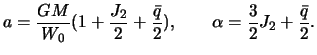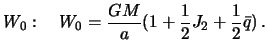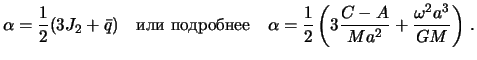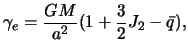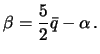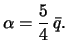<< 4.1 Potencial tyazhesti | Oglavlenie | 4.3 Gravitacionnye anomalii i ... >>
- 4.2.1 Osnovnye teoremy
- 4.2.2 Ellipsoid kak figura ravnovesiya
- 4.2.3 Model' "planety Rosha"
- 4.2.4 Sferoid Klero
- 4.2.5 Dva predela szhatiya dlya figur ravnovesiya
4.2 Figury ravnovesiya nebesnyh tel
Vse planety Solnechnoi sistemy nahodyatsya v sostoyanii, blizkom k
gidrostaticheskomu ravnovesiyu.
My uzhe govorili, chto planety s massoi bol'she 
t imeyut sharoobraznuyu
formu, potomu chto massy, slagayushie telo planet, obladayut svoistvom
plastichnosti. Planety priobretayut formu, kak esli by oni byli zhidkimi. V
etom sluchae urovennaya poverhnost' budet poverhnost'yu planety. V
deistvitel'nosti poverhnost' planety ne sovpadaet s urovennoi poverhnost'yu.
Eti otlichiya svidetel'stvuyut ob otkloneniyah ot sostoyaniya gidrostaticheskogo
ravnovesiya i yavlyayutsya predmetom izucheniya geofizikov i geodezistov. Vvedeny
special'nye terminy tlya oboznacheniya poverhnostei urovnya dlya planet.
Ekvipotencial'naya poverhnost' Zemli, po predlozheniyu Listinga, nazyvaetsya
geoidom. Po analogii, urovennuyu poverhnost' dlya Luny nazyvayut selenoidom, urovennuyu poverhnost'
Marsa -- areoidom, i t.p
4.2.1 Osnovnye teoremy
Teorema Lyapunova
Edinstvenno ustoichivoi figuroi ravnovesiya pokoyasheisya zhidkosti yavlyaetsya sfera.
Sledstviem etoi teoremy mozhno usmotret' sharoobraznost' vseh planet Solnechnoi sistemy.
Teorema Puankare
Edinstvenno vozmozhnym dvizheniem zhidkosti, nahodyasheisya v sostoyanii otnositel'nogo ravnovesiya, yavlyaetsya ravnomernoe vrashenie vokrug odnoi iz glavnyh osei inercii. Ponyatno, chto v sluchae, kogda planeta blizka k sostoyaniyu gidrostaticheskogo ravnovesiya, ee os' vrasheniya pochti sovpadaet s glavnoi os'yu inercii.
Teorema Lihtenshteina
Figura ravnovesiya odnorodnoi zhidkosti vsegda simmetrichna otnositel'no ploskosti, prohodyashei cherez centr inercii i perpendikulyarnoi k osi vrasheniya.
Etu teoremu nazyvayut eshe teoremoi o sushestvovanii ekvatora.
Issledovaniya pokazali, chto potencial prityazheniya gidrostaticheski ravnovesnoi planety soderzhit lish' chetnye zonal'nye garmoniki :
prichem mul'tipol'nye momenty 
ubyvayut kak 
4.2.2 Ellipsoid kak figura ravnovesiya
Kak my uzhe govorili, vnutri odnorodnogo ellipsoida, kak i dlya shara, sila
prityazheniya podchinyaetsya zakonu Guka: ona pryamo proporcional'na otkloneniyu
material'noi tochki ot polozheniya ravnovesiya. V teorii potenciala dokazano,
chto silovaya funkciya dlya vnutrennei tochki imeet vid
.
Togda komponenty sily prityazheniya proporcional'ny
koordinatam prityagivaemoi tochki
. Zdes'
, 
, 
i 
-- postoyannye, zavisyashie ot plotnosti i parametrov ellipsoida i
ne zavisyashie ot koordinat tochki. Privedem eti formuly bez vyvoda
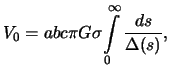
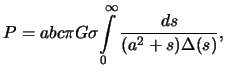
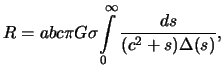
gde
Esli prityagivaemaya material'naya tochka -- vneshnyaya, to dlya nee silovaya funkciya
sohranyaet tot zhe vid, no
perestayut byt' postoyannymi, a
zavisyat ot koordinat tochki. Dlya ih vychisleniya spravedlivy te zhe integraly,
chto i dlya vnutrennei tochki, no nizhnii predel ne nul', a velichina 
,
kotoraya vybiraetsya takim obrazom, chtoby ellipsoid
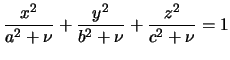
prohodil cherez zadannuyu vneshnyuyu tochku.
Potencial tyazhesti ot potenciala prityazheniya otlichaetsya tem, chto additivno soderzhit potencial
centrobezhnoi sily
. Podstavlyaya syuda vyrazhenie dlya potenciala prityazheniya
ellipsoida, poluchim
Esli poverhnost' ellipsoida yavlyaetsya poverhnost'yu urovnya, to takoi ellipsoid
budet gidrostaticheski ravnovesnym. Uravneniem urovennoi poverhnosti budet
, gde 
-- postoyannaya velichina. Voznikaet vopros,
mozhno li podobrat' takuyu uglovuyu skorost' vrasheniya dlya trehosnogo ellipsoida
s zadannymi poluosyami, chtoby ego poverhnost' okazalas' poverhnost'yu urovnya? Netrudno
ubedit'sya, chto nel'zya.
Uravneniem trehosnogo ellipsoida v dannom sluchae budet vyrazhenie
Opredelim bol'shie poluosi
Ochevidno, chto esli iz pervogo uravneniya my opredelim uglovuyu skorost', to sovsem ne obyazatel'no, chtoby eta uglovaya skorost' udovletvoryala vtoromu uravneniyu. Tem ne menee specialistami v oblasti teorii figur ravnovesiya nebesnyh tel dokazano sushestvovanie ravnovesnyh trehosnyh ellipsoidov, kotorye poluchili nazvanie ellipsoidov Yakobi.
4.2.2.1 Ellipsoid Maklorena
V chastnom sluchae 
, poetomu 
. Iz uravnenie (4.6) poluchim
Poluchennye uravneniya opredelyayut i postoyannuyu
i 
. Po-vidimomu, dlya lyubyh zadannyh poluosyah
ellipsoida vrasheniya mozhno naiti uglovuyu skorost' vrasheniya, takuyu, chto dannyi
ellipsoid stanovitsya figuroi ravnovesiya.
4.2.3 Model' "planety Rosha"
Pod "planetoi Rosha" my budem ponimat' takuyu figuru ravnovesiya, v kotoroi vsya prityagivayushaya massa sosredotochena v i odnoi tochke -- centre mass, a vektor sily tyazhesti obrazuyut vektornaya summa sily prityazheniya i centrobezhnoi sily. Togda uravneniem "poverhnosti" takoi planety budet
Rassmotrim, snachala, kak vyglyadit poverhnost' urovnya vblizi nachala
koordinat. V etom sluchae velichinu
mozhno
schitat' maloi, a , naoborot, bol'shoi. Prenebregaya v (4.8) vtorym
slagaemym v levoi chasti formuly, poluchim
. Eto
uravnenie zamknutoi poverhnosti, kotoraya po mere priblizheniya k nachalu
koordinat stanovitsya vse bolee pohozhei na sferu. Nazovem ee psevdosferoi.
Po mere otdaleniya ot nachala koordinat v ploskosti 
my dostignem takih
tochek, v kotoryh sila prityazheniya i centrobezhnaya sila stanovyatsya ravnymi i
protivopolozhno napravlennymi, to est'
,
Otsyuda
. My poluchili uravnenie okruzhnosti s
radiusom, ravnym
Ponyatno, chto vo vseh
tochkah etoi okruzhnosti sily tyazhesti ravna nulyu.
Esli dvigat'sya dal'she ot nachala koordinat, my pridem k variantu, kogda
budet bol'shoi velichinoi, a 
, naoborot, maloi. Togda
prenebregaya pervym chlenom v formule (4.8), poluchim uravnenie poverhnosti,
blizkoi k krugovomu cilindru
.
Eto uzhe razomknutaya poverhnost' urovnya. Planety s takoi poverhnost'yu
sushestvovat' ne mozhet.
Takim obrazom, gidrostaticheski ravnovesnaya planeta mozhet sushestvovat' tol'ko vnutri "polosti Rosha", gde sila tyazhesti vsyudu otlichna ot nulya i napravlena po normali vnutr' etoi poverhnosti. Poverhnost' takoi planety imeet oval'nuyu formu, splyusnutuyu s polyusov.
4.2.4 Sferoid Klero
Sferoidom v geodezii nazyvayut poverhnost' vrasheniya, blizkuyu k sfere. V pervom priblizhenii v kachestve uravneniya sferoida mozhno prinyat'
Ochevidno, chto na ekvatore 
, a na polyusah
,
. Figura, uravnenie
kotoroi udovletvoryaet formule (4.9) obladaet szhatiem: polyarnyi radius ee men'she
ekvatorial'nogo. Iz opredeleniya sleduet, chto
.
Ustanovim svyaz' mezhdu koefficientom 
i szhatiem planety. Iz formuly
(3.18) sleduet, chto potencial prityazheniya raven
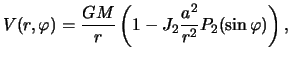
a potencial tyazhesti --
V privedennoi formule my ogranichilis' lish' koefficientom , otbrosiv
vse ostal'nye mul'tipol'nye momenty, tak kak v sluchae gidrostaticheski
ravnovesnoi figury, oni budut imet' bolee vysokii poryadok malosti, chem
postoyannaya .
Vvedem oboznachenie
. Novaya malaya velichina est', grubo govorya,
otnoshenie centrobezhnoi sily na ekvatore k sile prityazheniya. Sledovatel'no
. Podstavim poluchennoe
vyrazhenie v (4.10) i vynesem za obshie skobki otnoshenie :
Priravnivaya poluchennoe vyrazhenie postoyannoi , poluchim uravnenie
sferoida.
Teorema Klero ustanavlivaet svyaz' mezhdu parametrami sferoida, siloi tyazhesti na ego poverhnosti i koefficientami razlozheniya gravitacionnogo potenciala.
Szhatie sferoida Klero.
Sravnim formulu (4.11) s (4.9).
Uchityvaya, chto
-- malye
velichiny, zapishem priblizhennoe ravenstvo
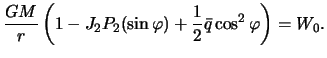
Reshim poluchennoe vyrazhenie otnositel'no 
Chtoby otozhdestvit' poluchennuyu formulu s uravneniem sferoida (4.9), primem vo vnimanie, chto
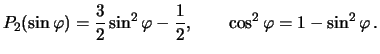
Postavlyaya eti ravenstva v (4.12), poluchim
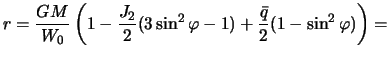
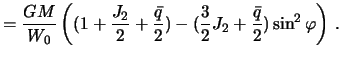
Sravnivaya poluchennoe vyrazhenie s (4.9) i uchityvaya, chto
i 
-- malye velichiny, poluchim
Otsyuda opredelyaem postoyannuyu
Itak, pervaya chast' teoremy Klero ustanavlivaetsya svyaz' mezhdu szhatiem ravnovesnoi planety s pervym koefficientom zonal'noi garmoniki razlozheniya gravitacionnogo potenciala i uglovoi skorost'yu vrasheniya planety.
Vtoraya chast' teoremy Klero opredelyaet zavisimost' sily tyazhesti na poverhnosti ravnovesnoi planety ot shiroty.
Sila tyazhesti na poverhnosti sferoida Klero.
Vernemsya snova k formule potenciala tyazhesti dlya sferoida (4.11). Dlya togo, chtoby poluchit' silu tyazhesti nam nuzhno potencial prodifferencirovat' po normali k poverhnosti urovnya. Odnako, poskol'ku nash sferoid malo otlichaetsya ot sfery, differencirovanie po normali my zamenim differencirovaniem po radius-vektoru, chto znachitel'no proshe.
Oboznachiv proizvodnuyu po radius-vektoru bukvoi 
, poluchim
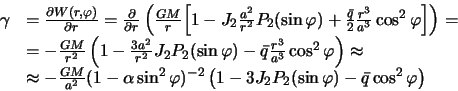
S tochnost'yu do malyh velichin pervogo poryadka budem imet'
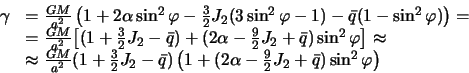
Sila tyazhesti na ekvatore, soglasno poluchennoi formule, ravna
a dlya lyuboi shiroty
gde
.
S pomosh'yu (4.15)
isklyuchim :
, to est'
zdes'
.
Formulami (4.17) i (4.18) my i zavershim izlozhenie teoremy Klero.
4.2.5 Dva predela szhatiya dlya figur ravnovesiya
Kosnemsya snachala istorii nashego voprosa. I.N'yuton (1643-1727) dlya ob'yasneniya
yavleniya, kotoroe zametili mnogoe astronomy, ot'ezzhayushie v ekspedicii dlya
nablyudenii solnechnogo zatmeniya v ekvatorial'nuyu zonu, astronomicheskie chasy
mayatnikovogo tipa otstayut po sravneniyu s Parizhskoi observatoriei, gde oni
strogo vyveryalis', na 2,5 minuty v sutki. N'yuton predpolozhil, chto vinoi tomu
sluzhit ellipsoidal'naya forma Zemli i, estestvenno, ee sutochnoe vrashenie.
Predpolagaya, chto Zemlya -- odnorodnyi ellipsoid vrasheniya, on poluchil, chto
szhatie zemnogo ellipsoida dolzhno byt' ravnym 1,25 
=1:230.
Sovremennik N'yutona Gyuigens (1629-1695) reshaet tu zhe zadachu, no drugim
putem. On predpolozhil, chto sily prityazheniya napravleny k centru, a ellipsoidal'nost'
poverhnosti urovnya voznikaet tol'ko za schet centrobezhnoi sily. Takim
obrazom, esli N'yuton v kachestve figury ravnovesiya bral ellipsoid Maklorena,
to Gyuigens -- figuru, kotoruyu my nazvali "planetoi Rosha". On poluchil, chto
szhatie ravno 0.5 = 1:576. Rezul'tat, kotoryi znachitel'no otlichaetsya
N'yutonovskoi ocenki szhatiya.
Vernemsya k teorii Klero. Soglasno ego teorii szhatie ravnovesnoi planety
dolzhno byt' ravno
. Pervyi predel szhatiya poluchim, esli primem Zemli odnorodnym
dvuhosnym ellipsoidom, dlya kotorogo
,
. Otsyuda
.
No
,
,
.
Sledovatel'no
i, nakonec,
My poluchili to zhe znachenie, chto i N'yuton, pravda s tochnost'yu do pervoi stepeni szhatiya.
Vtoroi predel szhatiya, my poluchim, esli budem schitat' vse prityagivayushie massy
sharom, togda 
i
Takim obrazom. real'noe szhatie lezhit mezhdu etimi dvumya predelami
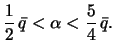
Dlya illyustracii skazannogo privedem szhatiya nekotoryh planet Solnechnoi sistemy, a takzhe ih vozmozhnye predel'nye znacheniya
Sravnivaya znacheniya szhatiya, my vidim, chto figura planety v znachitel'no stepeni zavisit ot ee vnutrennego stroeniya. Planety Zemlya i Mars ves'ma daleki ot togo stroeniya, kotoroe prinyal Gyuigens: planeta imeet kompaktnoe tverdoe prityagivayushee telo, okruzhennoe ryhloi obolochkoi. Po velichine szhatiya mozhno sudit' o tom, chto k takoi modeli bolee podhodyat planety giganty.
Privedennye dannye vzyaty iz knigi akad. A.A. Mihailova "Kurs gravimetrii i teorii figury Zemli", opublikovannoi v 1939 godu. Sovremennye dannye mogut neskol'ko otlichat'sya ot privedennyh, hotya obshaya kartina ne izmenitsya.
<< 4.1 Potencial tyazhesti | Oglavlenie | 4.3 Gravitacionnye anomalii i ... >>
|
Publikacii s klyuchevymi slovami:
gravimetriya - geofizika - solnechnaya sistema - seismologiya
Publikacii so slovami: gravimetriya - geofizika - solnechnaya sistema - seismologiya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
