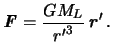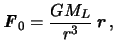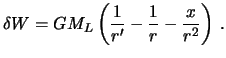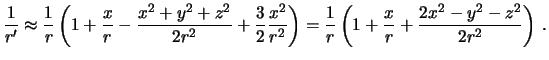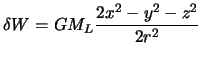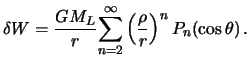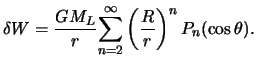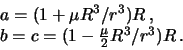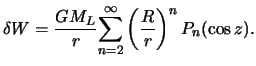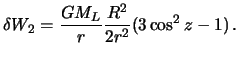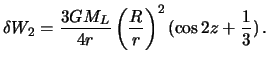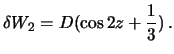<< 5.2 Temperatura v nedrah | Oglavlenie | 6.2 Tipy prilivnyh voln >>
6. Prilivy
Razdely
- 6.1 Prilivoobrazuyushii potencial
- 6.2 Tipy prilivnyh voln
- 6.3 Nablyudeniya prilivnyh yavlenii na Zemle
- 6.4 Kosmogonicheskoe znachenie issledovaniya prilivov
6.1 Prilivoobrazuyushii potencial
Podrazdely- 6.1.1 Prilivnaya deformaciya urovennoi poverhnosti planety
- 6.1.2 Preobrazovanie formuly dlya prilivoobrazuyushego potenciala
Vsem horosho izvesten morskoi priliv, kogda dva raza v sutki voda podnimaetsya u morskih beregov, zatem vnov' otkatyvaetsya ot berega. No priliv sushestvuet ne tol'ko na more, no i na sushe. Dva raza v sutki poverhnost' zemli, na kotoroi vystroeny vse doma, ulicy, dorogi, podnimayutsya i opuskayutsya. V Moskve amplituda etih kolebanii sostavlyaet priblizitel'no 0,5 m. No my etogo ne zamechaem. Otchego eto proishodit?
Kak izvestno, rezul'tatom deistviya sily na telo yavlyaetsya libo ego uskorenie, esli ono svobodno i ne vzaimodeistvuet s drugimi telami, libo ego deformaciya, esli takoe vzaimodeistvie sushestvuet. Prityazheniya Luny i Solnca nashei planety soobshayut ei uskorenie, kotoroe ona imeet, sovershaya dvizhenie po orbite. Odnako ne vse chasti planety ispytyvayut odinakovoe prityazhenie. V kachestve prityagivayushego tela voz'mem poka tol'ko Lunu. Maksimal'noe prityazhenie Lunoi ispytyvayut te chasti Zemli, dlya kotoryh ona nahoditsya strogo v zenite, a minimal'noe -- v nadire. Centr mass Zemli nahoditsya v promezhutochnom polozhenii. Rezul'tiruyushaya sila prityazheniya planety prilozhena k centru mass. Ona soobshaet Zemle postupatel'noe uskorenie. Dlya opisaniya processov v sisteme otscheta, svyazannoi s Zemlei, to est' v neinercial'noi sisteme koordinat, krome upomyanutyh sil prityazheniya neobhodimo vvesti silu inercii, ravnuyu masse kakogo-libo probnogo tela umnozhennuyu na uskorenie sistemy otscheta i napravlennuyu v storonu, protivopolozhnuyu uskoreniyu sistemy otscheta.
Prenebregaya razmerom, stroeniem i formoi Luny, zapishem udel'nuyu silu
prityazheniya probnogo tela, nahodyashegosya na Zemle. Pust' 
-- radius-vektor, napravlennyi ot probnogo tela v storonu Luny, -- dlina
etogo radius-vektora, togda sila prityazheniya etogo tela Lunoi budet ravna
Zdes' 
-- selenocentricheskaya gravitacionnaya postoyannaya. Probnoe telo
pomestim v tochku 
. Sila prityazheniya probnogo tela pomeshennogo v centr
mass Zemli budet ravna
gde
i 
sootvetstvenno radius-vektor, soedinyayushii centry mass
Zemli i Luny, i ego absolyutnaya velichina. Togda prilivnoi siloi nazyvaetsya raznost' etih
dvuh sil prityazheniya
V formulah (6.1) i (6.2) prityagivayushee telo (Luna) rassmatrivaetsya kak material'naya tochka ili shar so sfericheski simmetrichnym raspredeleniem mass
Silovaya funkciya prityazheniya probnogo tela Lunoi nichem ne otlichaetsya ot
silovoi funkcii prityazheniya shara (material'noi tochki), to est' ona ravna
. Chto kasaetsya vtoroi sily, prilozhennoi k centru mass i
yavlyayusheisya siloi inercii dlya vseh material'nyh tochek Zemli, to ona strogo
postoyannaya. Dlya polucheniya silovoi funkcii dlya etoi sily nam neobhodimo
vvesti vremennuyu sistemu koordinat. Os' Ox provedem iz centra Zemli i napravim
v storonu Luny. Napravleniya dvuh drugih osei -- proizvol'nye. Togda silovaya
funkciya dlya sily
, ochevidno, ravna
. Prilivoobrazuyushii potencial raven raznosti etih dvuh silovyh funkcii. Oboznachiv ego cherez
, budem imet'
Postoyannuyu
opredelim pri uslovii, chto prilivoobrazuyushii potencial v centra
Zemli raven nulyu. Pri etom 
, 
.
Poetomu
. Sledovatel'no, dlya
prilivoobrazuyushego potenciala mozhno zapisat'
Poskol'ku
, to
.
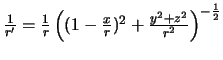Polagaya otnosheniya
malymi, poslednee vyrazhenie mozhno predstavit' sleduyushim
obrazom
Podstavim poluchennoe vyrazhenie v (6.4), poluchim
Vyrazhenie dlya prilivoobrazuyushego potenciala mozhno utochnit', esli v (6.4)
otnoshenie 
zamenit' razlozheniem v ryad po polinomam Lezhandra, podobno tomu,
kak my delali pri vyvode gravitacionnogo potenciala planety.
Pust' 
--
rasstoyanie tochki ot centra planety ( ot nachala sfericheskoi sistemy
koordinat), a 
-- geocentricheskoe zenitnoe rasstoyanie prityagivayushego tela
(Luny), togda
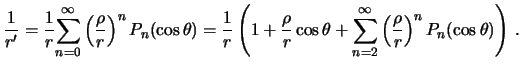
Poskol'ku
, poluchim
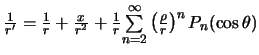. Postavlyaya poluchennoe vyrazhenie v formulu dlya prilivoobrazuyushego
potenciala (6.4), okonchatel'no poluchim
Ostaetsya opredelit' prilivoobrazuyushii potencial na poverhnosti planety.
Poskol'ku na poverhnosti sfericheskoi planety 
, to
6.1.1 Prilivnaya deformaciya urovennoi poverhnosti planety
Prilivnoe vozmushenie potenciala neizbezhno deformiruet urovennuyu poverhnost'
planety. Vypolnim priblizhennuyu ocenku etih iskazhenii. Dlya prostoty budem
schitat', chto Zemlya shar so sfericheski simmetrichno raspredelennoi massoi.
Togda ee nevozmushennyi gravitacionnyi potencial na poverhnosti planety imeet
prostoi vid 
. Dlya tochki , nahodyasheisya na rasstoyanii ot centra sfery
gravitacionnyi potencial Zemli raven 
.
Dobavlyaya syuda prilivnoi potencial,
poluchim vozmushennuyu poverhnost' urovnya
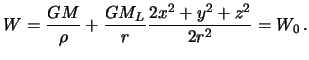
V kachestve konstanty my voz'mem nevozmushennyi gravitacionnyi potencial na poverhnosti. Togda, posle deleniya na gravitacionnuyu postoyannuyu, poluchim
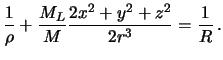
Zdes' peremennymi velichinami yavlyayutsya 
i .
Oboznachim otnoshenie mass
gravitiruyushego tela k masse planety grecheskoi bukvoi 
i reshim poluchennoe
vyrazhenie otnositel'no :
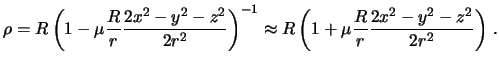
Tak kak
, s toi zhe stepen'yu tochnosti
poluchim
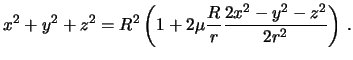
Preobrazuem poluchennoe vyrazhenie
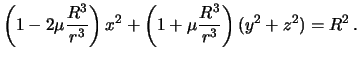
Uchityvaya, chto otnosheniya 
-- malye velichiny poslednee vyrazhenie mozhno
perepisat' tak
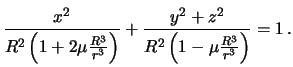
My poluchili uravnenie dvuhosnogo ellipsoida, u kotorogo os' vrasheniya
sovpadaet s os'yu 
, to est' s pryamoi, soedinyayushei prityagivayushee telo s centrom
Zemli. Poluosi etogo ellipsoida, ochevidno, ravny
Itak, urovennaya poverhnost', zadannaya v vide shara, vsledstvie prilivnogo
deistviya drugogo nebesnogo tela vytyagivaetsya v storonu etogo tela i
prevrashaetsya v ellipsoid vrasheniya. Bol'shaya poluos' budet prevyshat' radius
planety na velichinu
, a malye poluosi budut men'she radiusa na velichinu
.
Zametim, kstati, chto s toi zhe stepen'yu tochnosti proizvedenie vseh treh
poluosei ostayutsya postoyannymi, chto govorit o neizmennosti ob'ema,
ogranichennogo poverhnost'yu urovnya.
Dlya illyustracii skazannogo privedem chislennyi primer. Vychislim prilivnoi
"gorb" na Zemle, vyzvannyi prityazheniem Luny. Radius Zemli raven
= 6378 km,
rasstoyanie mezhdu centrami Zemli i Luny ravno
km,
otnoshenie mass Luna/Zemlya ravno 1:81. Podstavlyaya eti dannye v formulu dlya
uvelicheniya bol'shoi poluosi, poluchim 0,36 m Netrudno podschitat', chto na Lune
analogichnyi prilivnoi gorb, napravlennyi v storonu Zemli budet raven 13 m.
Neobhodimo podcherknut', chto v privedennyh rassuzhdeniyah ne uchityvaetsya prilivnye deformacii samoi Zemli, chto takzhe izmenit poverhnost' urovnya. Dlya strogih vykladok neobhodimo zadat' model' Zemli, ee stroenie, uprugie postoyannye i t.p., chto, konechno, vyhodit daleko za ramki nashego kursa.
6.1.2 Preobrazovanie formuly dlya prilivoobrazuyushego potenciala
Vernemsya k formule (6.10). Zdes' argumentom polinomov Lezhandra yavlyaetsya
geocentricheskoe zenitnoe rasstoyanie prityagivayushego nebesnogo tela .
Rassmotrim treugol'nik OPL. Storona OR,
kak my znaem, ravna radiusu Zemnogo shara
(esli tochka P nahoditsya na poverhnosti zemnogo
shara), storona OL ravna rasstoyaniyu mezhdu centrami mass prityagivayushego i
prityagivaemogo tela , ugol mezhdu etimi storonami raven geocentricheskomu
zenitnomu rasstoyaniyu , ugol mezhdu storonami PL
i prodolzheniem storony OR raven
zenitnomu rasstoyaniyu z. Proekciya storony OL na prodolzhenie storony
OR ravna
. Otsyuda
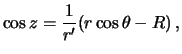
Mozhno li zamenit' geocentricheskoe zenitnoe rasstoyanie topocentricheskim,
kotoroe ispol'zuetsya v astronomii? Kakuyu oshibku my sdelaem, esli zamenim v
formule (6.8) ugol zenitnym rasstoyaniem 
? Ochevidno, chto my dolzhny ocenit'
velichinu
Pust' otnoshenie 
yavlyaetsya maloi velichinoi, togda
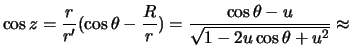
sledovatel'no
. Eta velichina maksimal'na pri
.
Tak esli gravitiruyushee telo --
Luna, to 
=6.371/384.4=0.0166. Sledovatel'no, maksimal'noe iskazhenie
zenitnogo rasstoyaniya v sisteme Zemlya-Luna ne prevoshodit 1,7%. Dlya
bol'shinstva zadach etim otlichiem mozhno prenebrech' i v kachestve
prilivoobrazuyushego potenciala brat'
Ponyatno, chto naibol'shii vklad v prilivnye yavleniya sozdaet pervyi chlen formuly (6.10). Ochen' chasto im i ogranichivayutsya, hotya pri strogom analize prilivnyh yavlenii prihoditsya uchityvat' i ostal'nye chleny razlozheniya (6.10).
Itak, prilivoobrazuyushii potencial s tochnost'yu do
imeet vid
Vypolnim nekotorye preobrazovaniya poluchennoi formuly i privedem k
obsheprinyatomu vidu. Poskol'ku
,
to podstavlyaya eto vyrazhenie v formulu (6.11) osle neslozhnyh preobrazovanii,
poluchim
Velichina
nazyvaetsya postoyannoi Dudsona.
Teper' vmesto (6.12) mozhno
zapisat'
Zametim, chto tak nazyvaemaya postoyannaya Dudsona vovse ne yavlyaetsya, postoyannoi velichinoi, tak kak rasstoyanie mezhdu prityagivayushim i prityagivaemym telami izmenyayutsya iz-za togo chto oni dvizhutsya po orbitam, strogo govorya, ne ellipticheskim, podchinyayas' zakonam nebesnoi mehaniki. V knige bel'giiskogo uchenogo P. Mel'hiora izvestnogo specialista po prilivam privodyatsya chislennye znacheniya postoyannyh Dudsona:
| dlya Luny |  = 2,6206 m
  , |
| dlya Solnca | = 1,2035 m
. |
<< 5.2 Temperatura v nedrah | Oglavlenie | 6.2 Tipy prilivnyh voln >>
|
Publikacii s klyuchevymi slovami:
gravimetriya - geofizika - solnechnaya sistema - seismologiya
Publikacii so slovami: gravimetriya - geofizika - solnechnaya sistema - seismologiya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
