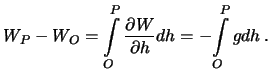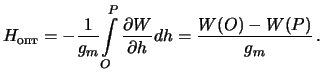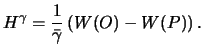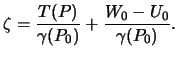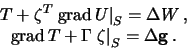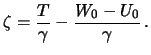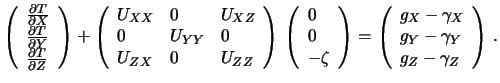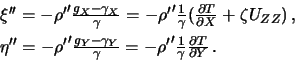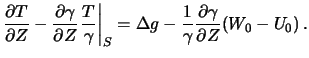<< Lekciya 8. Opredelenie figury geoida | Oglavlenie |
Lekciya 9. Kvazigeoid Molodenskogo
Osnovnye trudnosti resheniya problemy Stoksa. Problema regulyarizacii Zemli. Sistema vysot. Geodezicheskaya, ortometricheskaya i normal'naya vysoty. Kvazigeoid. Anomaliya vysoty. Telluroid. Kraevye usloviya zadachi Molodenskogo.
9.1 Kritika klassicheskoi teorii Stoksa
Primenenie formuly Stoksa dlya opredeleniya vysot geoida otnositel'no obshego zemnogo ellipsoida natalkivaetsya na ser'eznye trudnosti. Vo-pervyh, dlya integrirovaniya neobhodimo, chtoby gravitacionnye anomalii byli izvestny po vsei poverhnosti Zemli, bolee dvuh tretei kotoroi pokryta moryami i okeanami. Izmerenie sily tyazhesti na poverhnosti okeanov stalo vozmozhno lish' v HH stoletii.
V 1922-1929 gody gollandskii uchenyi F.A.Vening-Meines rabotal nad sozdaniem apparatury dlya izmereniya sily tyazhesti na podvizhnom osnovanii. Nakonec, v 1929 godu im byl sozdan okonchatel'nyi variant mayatnikovogo pribora s kotorym Vening-Meines sovershil plavanie na podvodnoi lodke v akvatoriyu yugo-vostochnoi Azii, gde v to vremya u Gollandii byli kolonii. Tochnost' gravimetricheskoi s'emki uchenyi ocenil v 3-4 mGal, chto bylo dostatochno dlya izucheniya sostoyaniya zemnoi kory v tom regione. Na osnovanii etih dannyh predlozhil novuyu teoriyu izostazii.
Uzhe v 1930 godu zaveduyushii kafedroi gravimetrii mehaniko-matematicheskogo fakul'teta MGU professor L.V.Sorokin sovershil pervoe plavanie v Chernom more takzhe na podvodnoi lodke s original'noi apparaturoi, izgotovlennoi v masterskih GAISh. V 1954 godu silami instituta VNIIGeofizika byl sozdan pervyi v mire morskoi gravimetr, a v 1955 godu proshel morskie ispytaniya na podvodnoi lodke vo vremya plavaniya vokrug Novoi Zemli. Rezul'taty ubeditel'no pokazali, chto tochnost' gravimetra ne ustupaet tochnosti mayatnikovogo pribora, trebuet gorazdo bolee prostoi obrabotki nablyudenii. Mayatnikovye pribory nazemnoi gravimetrii, kak izvestno, byli vytesneny gravimetrami, to zhe proizoshlo i s morskimi priborami. Morskie gravimetry seichas yavlyayutsya osnovnymi instrumentami morskoi gravimetrii. Vse men'she i men'she ostaetsya "belyh" pyaten na Zemle, gde sila tyazhesti neizvestna
Vtoraya problema -- bolee ser'eznaya. Teoriya Stoksa trebuet, chtoby vse massy lezhali pod urovennoi poverhnost'yu, nazyvaemoi geoidom. Krome togo, izmereniya sily tyazhesti vypolnyayutsya na fizicheskoi poverhnosti, ne sovpadayushei s geoidom. Zadacha sostoit v tom, chtoby v izmerennoi znachenie vnesti takie popravki, kotorye by perenesli vse massy pod uroven' morya, ne izmenyaya samoi urovennoi poverhnosti, a sila tyazhesti okazalas' by otnesennoi k urovnyu morya (geoidu). Eta problema shiroko obsuzhdalas' v nauchnoi literature i poluchila nazvanie problemy regulyarizacii Zemli.
Okazalos', chto dlya uspeshnogo resheniya problemy regulyarizacii neobhodimo znat' vnutrennee stroenie Zemli. V nauchnyi spor o tom, kak reshat' problemu regulyarizacii, v 50-h godah vmeshalsya M.S.Molodenskii, kotoryi dokazal, chto razlichnye varianty resheniya prakticheski ekvivalentny, no oni ne reshayut zadachu vpolne strogo. On predlozhil strogoe reshenie zadachi opredeleniya figury Zemli. Pri etom opredelyayutsya vysoty ne poverhnosti, kotoruyu my nazyvaem geoidom, a drugoi poverhnosti, dostatochno blizkoi k geoidu, kotoruyu on nazval kvazigeoidom.
M.S. Molodenskii razrabotal teoriyu postroeniya kvazieoida, predlozhil algoritmy priblizhennogo resheniya problemy. Vo-pervyh, redukciya (perenos) sily tyazhesti ili potenciala vypolnyaetsya v lineinom priblizhenii. Vo-vtoryh, hotya vse izmereniya i redukcii otnosyatsya k fizicheskoi poverhnosti ili k ellipsoidu, integrirovanie malyh funkcii, gde eto trebuetsya, vypolnyaetsya po sfere (sfericheskoe priblizhenie). Konechno, teoriya Molodenskogo ne okonchatel'naya. Ona postoyanno sovershenstvuetsya ego uchenikami. V Sovetskom Soyuze voznikla shkola Molodenskogo, kotoraya shiroko izvestna ne tol'ko u nas, no i za rubezhom.
9.2 Sistema vysot
Opredelit' figuru kakoi-libo poverhnosti -- eto znachit opredelit' rasstoyaniya kazhdoi tochki etoi poverhnosti do tela otscheta, za kotoroe beretsya ellipsoid vrasheniya. Eti rasstoyaniya obychno nazyvayut geodezicheskimi vysotami. Ponyatie vysoty, na pervyi vzglyad, ne trebuet utochneniya. Odnako eto ne tak. M.S.Molodenskii razrabotal celuyu sistemu vysot dlya geodezii.
Dopustim, chto imeem dve tochki 
i 
, prichem tochka vyshe tochki .
Esli soedinit'
eti tochki kanalom i pustit' vodu, kuda ona potechet? Kazhetsya vpolne
estestvennym otvet: iz tochki k tochke . Odnako eto ne sovsem tak. Ves'
vopros v tom, kak prohodit urovennaya poverhnost' cherez eti tochki. Esli obe
tochki lezhat na odnoi urovennoi poverhnosti, to voda nikuda ne potechet. Esli
urovennaya poverhnost', prohodyashaya cherez tochku okazhetsya pod urovennoi
poverhnost'yu tochki , to budet nablyudat'sya obratnaya kartina: voda potechet ot
tochki k tochke . Takim obrazom, dlya gidrotehnicheskih sooruzhenii sistema
geodezicheskih vysot okazyvaetsya neprigodnoi.
V geodezii vysoty opredelyayut nivelirovaniem. Nivelir -- eto opticheskaya truba, vizirnaya liniya kotoroi ustanavlivaetsya strogo gorizontal'no s pomosh'yu dostatochno vysoko chuvstvitel'nogo urovnya. Chtoby opredelit' prevyshenie odnoi tochki nad drugoi, v etih tochkah ustanavlivayutsya special'nye vertikal'nye reiki. S pomosh'yu nivelira s kazhdoi reiki poocheredno berut otschety, togda raznost' etih otschetov est' nivelirnoe prevyshenie odnoi tochki nad drugoi.
Nivelirnyi hod ot tochki 
,
raspolozhennoi, naprimer, na urovne morya, k tochke 
dast izmerennuyu
vysotu tochki nad urovnem morya
,
gde 
nivelirnoe
prevyshenie odnogo zvena. Esli nivelirnyi hod imeet mnogo zven'ev, to summu
mozhno zamenit' integralom
.
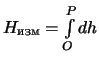Vychislim raznost' potencialov medu tochkami i .
Takim obrazom, dlya opredeleniya raznosti potencialov nuzhno imet' nivelirnye prevysheniya i silu tyazhesti vdol' vsego profilya.
Vvedem v rassmotrenie eshe odnu tochku. Cherez tochku prohodit silovaya liniya,
kotoruyu mozhno prodolzhit' do poverhnosti geoida (uroven' morya). Ona
peresechetsya s etoi poverhnost'yu v toke textitR'. Takim obrazom tochki
i R' lezhat na odnoi
poverhnosti urovnya (na geoide) Poskol'ku rezul'tat opredeleniya raznosti
potencialov ne zavisit ot puti integrirovaniya, vyberem takoi marshrut
O-R'-R. Prirashenie
potenciala my poluchim lish' na otrezke silovoi linii
R'-R:
.
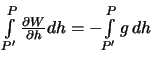Pri dvizhenii po silovoi linii sila tyazhesti nepreryvno menyaetsya. Soglasno
teoreme o srednem, v kurse matematicheskogo analiza, mozhno naiti takoe
znachenie podyntegral'noi funkcii, kotoroe ona prinimaet vnutri intervala
integrirovaniya, kotorym mozhno zamenit' podyntegral'noe vyrazhenie
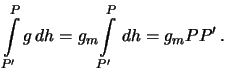
Otrezok silovoi linii RR'
nazyvaetsya ortometricheskoi vysotoi tochki
nad urovnem morya (to est' nad geoidom). Itak
Chtoby vychislit' ortometricheskuyu vysotu, neobhodimo znat' ne tol'ko
prirashenie potenciala, no i umet' vychislit' srednee znachenie sily tyazhesti na
otrezke silovoi linii, a dlya etogo neobhodimo znat' kak menyaetsya sila
tyazhesti na etom otrezke vnutri Zemli. M.S.Molodenskii predlozhil zamenit'
na srednee znachenie normal'no sily tyazhesti. Vysotu, kotoruyu my takim
obrazom poluchim on nazval normal'noi.
Takaya zamena neizbezhno vneset pogreshnost',
kotoraya, vprochem, nevelika. Soglasno opredeleniyu, normal'naya vysota mozhet
byt' opredelena po formule
Poskol'ku ortometricheskaya vysota est' vysota tochki nad urovnem morya, to malo otlichayushayasya ot nee normal'naya vysota budet ravna vysote tochki ot poverhnosti malo otlichayusheisya ot geoida. Molodenskii nazval etu poverhnost' kvazigeoidom.
Otlichie istinnoi (geodezicheskoi) vysoty ot normal'noi umestno nazvat' anomaliei vysoty. Eto ponyatie takzhe vvel Molodenskii. Itak, anomaliya vysoty est'
Anomaliya vysoty est' rasstoyanie kvazigeoida ot ellipsoida, ili ravna vysote
pochtigeoida. Ochevidno, chto
.
V klassicheskom ponimanii, opredelit'
figuru Zemli -- eto znachit opredelit' vysoty geoida 
.
Odnako, my ne sdelaem
bol'shoi pogreshnosti, esli budem schitat' figuroi Zemli -- figuru kvazigeoida,
a dlya etogo my dolzhny opredelit' anomalii vysot.
Svedem zadachu snova k kraevoi zadache dlya garmonicheskih funkcii. Sledovatel'no, anomaliyu vysoty nuzhno opredelit' cherez vozmushayushii potencial (sm lekciyu 8, razdel 8.1). Itak, imeem:
- potencial tyazhesti v tochke 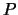raven
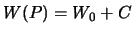, S -- prirashenie
potenciala ot urovnya morya (tochka );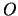
- normal'nyi potencial v tochke
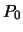, ravnyi
.
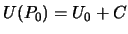Takim obrazom, tochka ne sovpadaet s tochkoi , tak kak ona podbiraetsya
tak, chtoby prirashenie potenciala real'nogo i normal'nogo byli odinakovymi
Zdes' postoyannye 
i 
oznachayut sleduyushee: pervaya postoyannaya
est' velichina potenciala tyazhesti na geoide, a vtoraya -- velichina normal'nogo
potenciala na urovennom ellipsoide. Netrudno ubedit'sya, chto otrezok 
raven anomalie vysoty 
. Sledovatel'no
.
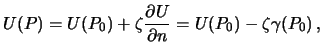
S drugoi storony
, poetomu
Otsyuda sleduet
My poluchili vnov' formulu Brunsa, odnako ona otlichaetsya tem, chto soderzhit
dopolnitel'nyi chlen
, kotoryi v "klassicheskoi" formule
otsutstvuet. V teorii Stoksa predpolagaetsya, chto obe eti postoyannye ravny:
potencial tyazhesti na urovne morya raven potencialu urovennogo ellipsoida.
Drugoe otlichie: normal'naya sila tyazhesti zadaetsya ne na geoide, a v nekotoroi
tochke 
otstoyashei ot tekushei toki na fizicheskoi poverhnosti na
velichinu, ravnuyu anomalii vysoty. Geometricheskoe mesto vseh tochek
nazyvaetsya telluroidom. Gravitacionnye anomalii, kak i prezhde, otnosyatsya k raznym
tochkam: nablyudennoe znachenie zadano na fizicheskoi poverhnosti, a normal'noe
-- na telluroide.
V literature, posvyashennoi issledovaniyu gravitacionnyh polei planet, vstrechayutsya i drugie opredeleniya ponyatiya telluroida, kak poverhnosti approksimiruyushuyu formu Zemli.
Telluroid Marussi opredelyaetsya sleduyushim obrazom.
Telluroid -- geometricheskoe mesto tochek, v
kotoryh potencial tyazhesti sovpadaet s normal'nym
.
Telluroid Krarupa (gravimetricheskii telluroid) -- geometricheskoe mesto tochek, v kotorom normal'naya sila tyazhesti sovpadaet
s siloi tyazhesti na poverhnosti Zemli
.
Kazhdoe iz opredelenii telluroida trebuet svoego podhoda dlya opredeleniya ego figury. My ostanovimsya zdes' lish' na telluroide i kvazigeoide Molodenskogo.
9.3 Kraevye usloviya zadachi Molodenskogo
V tochke na fizicheskoi poverhnosti Zemli nam izvestno znachenie potenciala
tyazhesti 
, a v tochke na telluroide -- znachenie normal'nogo
potenciala 
. Ispol'zuya vektorno-matrichnuyu matematiku zapishem
osnovnye sootnosheniya, svyazyvayushie vozmushayushii potencial 
raznost'
potencialov
, tak nazyvaemuyu anomaliyu
potenciala, anomaliyu vysoty i smeshannuyu anomaliyu sily tyazhesti
.
Netrudno videt', chto na telluroide Molodenskogo
,
na telluroide Marussi
, a na telluroide Krarupa
. V obshem sluchae imeem
Togda
ili
Analogichno poluchim smeshannuyu anomaliyu
no gradient vektora g est' gradient vseh ego sostavlyayushih, chto daet matricu-tenzor. Oboznachim
Zametim, chto raznost'
,
est' tak nazyvaemaya "chistaya" anomaliya,
ravna gradientu vozmushayushego potenciala
,
poetomu vmesto (9.8) mozhno zapisat'
Itak, my poluchili dva uravneniya, kotorye na fizicheskoi poverhnosti Zemli 
mozhno vzyat' v kachestve kraevyh uslovii
Pervaya iz privedennyh formul est' obobshenie formuly Brunsa, svyazyvayushei
vozmushayushii potencial s vysotoi kvazigeoida. Iz etih dvuh uravnenii mozhno
postroit' odno, esli isklyuchit' anomaliyu vysoty . Reshim vtoroe iz
privedennyh uravnenii. Predpolagaya, chto matrica
neosobaya,
poluchim
. Podstavim naidennoe reshenie v pervoe uravnenie.
Zametim, chto
Podstavlyaya poluchennoe vyrazhenie v pervoe uravnenie iz (9.10), budem imet'
Dlya uprosheniya zapisi, vvedem oboznachenie
.
Teper' kraevoe uslovie obobshennoi zadachi Molodenskogo prinimaet vid
9.3.1 Chastnyi sluchai: izmereniya vypolneny na urovennoi poverhnosti
Rassmotrim sluchai, kogda anomaliya potenciala -- postoyannaya velichina. Drugimi
slovami tochka , kak i v zadache Stoksa, nahoditsya na poverhnosti urovnya.
Togda
. Vyberem lokal'nuyu sistemu otscheta s nachalom v
tochke . Os' 
napravim na sever, os'
-- na vostok, a os' 
-- po napravleniyu vnutrennei
normali k ellipsoidu vniz.
Togda vektor anomalii vysoty mozhet byt' opredelen
matricei-strokoi
Gradienty normal'nogo potenciala v tochkah i ravny
Matrica vtoryh proizvodnyh normal'nogo potenciala
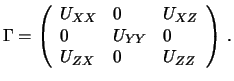
Pervoe iz uravnenii (9.10) dlya kraevyh uslovii daet
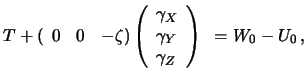
Vtoroe uravnenie iz (9.10) vyglyadit sleduyushim obrazom
Pervye dva uravneniya dayut ukloneniya otvesa
gde 
=206265 -- chislo sekund v radiane. Poslednii chlen v skobkah
formul (9.15) daet ochen' malyi vklad i mozhet byt' otbroshen.
Deistvitel'no,
my videli, chto dlya normal'noi sily tyazhesti maksimal'noe znachenie
gorizontal'nogo gradienta ravno 0,000811 mGal/m.
Pri =100 m, chto byvaet ochen' redko, velichina
sostavit 0,081 mGal i vneset pogreshnost' v uklonenie otvesa
0,017", togda kak ukloneniya otvesa dostigayut neskol'ko sekund dugi.
Tret'e uravnenie imeet vid
. Podstaviv syuda velichinu iz (9.13)
poluchim kraevoe uslovie dlya smeshannyh anomalii
My poluchili, takim obrazom, kraevoe uslovie pochti sovpadayushee s kraevym usloviem Stoksa.
Zadacha opredeleniya figury Zemli svoditsya k postroeniyu resheniya uravneniya Laplasa, kotoroe udovletvoryaet kraevomu usloviyu (9.16) ili, v obshem sluchae, usloviyu (9.12). Sposoby resheniya etoi zadachi zasluzhivayut special'nogo izucheniya, no vyhodyat za predely nashego kursa.
<< Lekciya 8. Opredelenie figury geoida | Oglavlenie |
|
Publikacii s klyuchevymi slovami:
gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya
Publikacii so slovami: gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
