<< Titul'nyi list | Oglavlenie | Lekciya 2. Geodezicheskie sistemy koordinat >>
Lekciya 1. Teoriya figury Zemli
Predmet teorii figury Zemli "Figury" i stroeniya planet. Geodinamika. Osnovnye ponyatiya fizicheskoi geodezii. Istoriya izucheniya figury Zemli. Kosmicheskaya geodeziya.
Figura planety... chto eto? Forma ee fizicheskoi poverhnosti? Forma ili figura? Voobshe govorya, eti dva slova ne ekvivalentny, esli ih primenyat' po otnosheniyu k planete. Termin figura Zemli vveden davno. Tak uchebnik prof. A.A.Mihailova, vpervye izdannyi v 1933 godu, nazyvaetsya "Kurs gravimetrii i teorii figury Zemli". Odnako ne on vvel etot termin. V tom zhe godu vyshel perevod knigi P.Picetti " Mehanicheskie osnovy figury planet " Original, estestvenno, vyshel ran'she. U A.A.Mihailova est' ssylka na knigu Buchholz H. Angewandte Mathematic. Das mechanische Potenzial und seine Anwendung zur Beschtimmung der Figur der Erde. Leipzig, 1916. Imeetsya ssylka i na bolee rannii istochnik: Todhunter J. A history of the mathematical Theory of Attraction and the Figure of the Earth. London, 1873. V tom zhe 1973 godu nemeckii fizik Listing predlozhil termin geoid dlya zamknutoi poverhnosti ravnogo potenciala. Takim obrazom, termin figura Zemli, kak pravilo, oboznachaet figuru ee urovennoi poverhnosti, prinyatoi v kachestve poverhnosti, otnositel'no kotoroi izmeryayutsya vysoty ee fizicheskoi poverhnosti.
Pod figuroi planety mozhno ponimat':
- --- Figuru ee fizicheskoi poverhnosti (geometricheskaya figura)
- --- Figuru ekvipotencial'noi poverhnosti (geoid, selenoid, areoid i t.p.)
- --- Dinamicheskuyu figuru planety, kotoroi yavlyaetsya central'nyi ellipsoid inercii.
Osobyi interes vyzyvayut figury gidrostaticheski ravnovesnyh tel. Esli predstavit' model' planety, sostoyashei iz koncentricheskih, tonkih sloev, imeyushih nekotoroe szhatie, to dlya gidrostaticheski ravnovesnyh tel davlenie vnutri kazhdogo sloya -- postoyanno. Otsutstvuyut gorizontal'nye sostavlyayushie sil davleniya, sposobnye sozdat' techeniya. Vertikal'naya sostavlyayushaya davleniya, obuslovlennaya sovokupnost'yu vneshnih (po otnosheniyu k rassmatrivaemoi tochke) sloev, kompensiruetsya reakciei podstilayushih sloev. V etom sluchae vypolnyaetsya uslovie
gde 
-- potencial gidrostaticheskogo davleniya, 
-- potencial tyazhesti,
-- plotnost'. Eto sootnoshenie vypolnyaetsya dlya vseh tochek tela planety, vklyuchaya
ee vneshnyuyu poverhnost'. V poslednem sluchae uslovie
opredelyaet i fizicheskuyu poverhnost' modeli planety.
Zadacha issledovaniya vnutrennego stroeniya planety chasto svoditsya k soglasovaniyu ee teoreticheskogo i nablyudennogo potenciala tyazhesti. Pri etom ee gidrostaticheskoe ravnovesie prinimaetsya kak gipoteza. Otsyuda yasno, chto teoriya figur ravnovesiya nebesnyh tel, yavlyayushayasya odnim iz krupnyh razdelov nebesnoi mehaniki, imeet fundamental'noe znachenie.
Otlichiya modeli ot gidrostaticheski ravnovesnoi figury ne obyazatel'no ukazyvayut na neadekvatnost' prinyatoi modeli real'noi planete. Eti otlichiya mogut byt' i istochnikom informacii o vnutrennih silah, sozdayushih napryazheniya sdviga ili rastyazheniya. Pri tekuchesti materiala eti napryazheniya sozdadut konvekcionnye techeniya, kotorye nahodyat otrazhenie v teplovyh i magnitnyh polyah planety. Krome togo, eti yavleniya ne mogut ne vliyat' na vrashenie planety, na dvizhenie otdel'nyh blokov ee poverhnosti. Nablyudeniya za izmeneniem form poverhnosti dostupny geodezii i yavlyayutsya odnim iz vazhneishih predmetov ee izucheniya.
Na styke nauk -- geodezii, geofiziki i astronomii -- voznikla
geodinamika, ob'edinyayushaya
kinematicheskuyu i dinamicheskuyu geodezii (terminologiya M.S.Molodenskogo). V
pervom sluchae izuchayut dvizhenie, vo vtorom -- sily. Seichas nauki o Zemle ochen'
mnogo udelyayut vnimaniya geodinamicheskim issledovaniyam, kotorye pomogayut
pravil'no osmyslit' medlennye evolyucionnye processy, predskazyvat'
zemletryaseniya i podderzhivat' vysokuyu tochnost' astronomo-geodezicheskih setei.
Geodinamicheskie variacii dostigayut velichin
v god, to
est' 0,6-0,7 sm smesheniya, 1-10 mkGal variacii sily tyazhesti,
0,0002-0,02" otklonenii otvesnoi linii.
Vernemsya k figure Zemli. Real'naya figura planety, estestvenno, otlichaetsya ot ellipsoidal'noi. Fizicheskaya poverhnost' Zemli, da i lyuboi planety nastol'ko slozhna, chto ona ne poddaetsya strogomu matematicheskomu opisaniyu. Naibolee naglyadnoe predstavlenie -- karta vysot etoi poverhnosti nad urovnem morya ili geoida -- poverhnosti ravnogo potenciala tyazhesti, prohodyashaya cherez nachalo otscheta vysot. Eta poverhnost' blizka k nevozmushennoi poverhnosti vodnoi gladi okeanov i soobshayushihsya s nimi morei. Odnako, iz-za razlichiya temperatury i solenosti, atmosfernogo davleniya i t.p. poverhnost' vodnoi gladi ne sovpadaet strogo s geoidom, a otklonyaetsya priblizitel'no v predelah odnogo metra. Naprimer, v zone Panamskogo kanala raznost' urovnei Tihogo i Atlanticheskogo okeanov sostavlyaet 62 sm.
Dlya postroeniya karty vysot nuzhno poverhnost' urovnya okeanov prodolzhit' pod kontinenty. Sdelat' eto ne prosto: neobhodimo znat' raspredelenie plotnostei gornyh porod. Eta trudnost' byla preodolena M.S.Molodenskim: vmesto geoida on predlozhil stroit' kvazigeoid, chto ne trebuet znaniya vnutrennego stroeniya zemnoi kory.
Geodeziya -- v perevode s grecheskogo zemlerazdelenie -- raspolagaet priborami dlya opredeleniya uglov i rasstoyanii, to est' imeet delo s geometricheskimi velichinami. Odnako dlya postroeniya kvazigeoida trebuetsya znat' i udel'nuyu silu tyazhesti, to est' gravitacionnoe pole. Poetomu etot razdel geodezii nazyvayut fizicheskoi geodeziei. Zadachei fizicheskoi geodezii yavlyaetsya ne tol'ko postroenie figury poverhnosti planety ili ee geoida (selenoida, areoida i t.p.), no i izuchenie geometrii silovyh linii v prostranstve, otklonenii otvesa, harakteristik gravitacionnogo potenciala i ego vzaimodeistviya s drugimi fizicheskimi polyami. Termin fizicheskaya geodeziya, pozhalui, mozhno otozhdestvit' s terminom teoriya figury Zemli, esli etot predmet ponimat' bolee shiroko, chem ukazano v ego nazvanii.
Kratkii istoricheskii obzor
Chto takoe nasha Zemlya? Kakoi ona formy? Etimi voprosami interesovalis' na samoi zare probuzhdeniya soznaniya. Do nas doshli svedeniya, chto Pifagor, zhivshii v V1 veke do nashei ery, schital Zemlyu sharom. Ego pochemu-to ne smushal vopros, kak zhe uderzhivayutsya vse predmety na "pokatoi" poverhnosti shara. Dva veka spustya velikii Aristotel' pryamo ukazal na dokazatel'stvo sharoobraznosti Zemli. Eto -- lunnye zatmeniya. Zemlya brosaet ten' na Lunu, kogda Solnce nahoditsya s protivopolozhnoi storony. A eta ten' -- kruglaya! Eshe odin grecheskii uchenyi Eratosfen, zhivshii v tret'em veke do nashei ery, predprinyal pervuyu popytku opredelit' radius Zemnogo shara. On ocenil dlinu dugi meridiana mezhdu Aleksandriei i Assuanom (Sienoi) i vospol'zovalsya tem, v den' letnego solncestoyaniya Solnce v Assuane stoit tochno v zenite. Ono mozhet "zaglyanut'" dazhe v samye glubokie kolodcy. V eto zhe vremya v Aleksandrii naimen'shee zenitnoe rasstoyanie Solnca sostavlyaet 1/50 dolyu okruzhnosti. Mezhdu Aleksandriei i Assuanom sushestvoval karavannyi put' dlinoi v 5000 stadii, to est' priblizitel'no 800-900 km. Tochnaya dlina stadii neizvestna, polagayut, chto ona ravna 0,158-0,185 km. Umnozhaya 5000 na 50, Eratosfen poluchil dlinu meridiana, ravnuyu 250000 stadii. Radius Zemli, v etom sluchae, budet raven 40000 stadii, to est' 6000-7400 km. Sovremennoe znachenie srednego radiusa Zemli ravno 6371,023 km. Tak chto rezul'tat Eratosfena neplohoi.
Pervye izmereniya razmerov Zemli byli osnovany na izmerenii dlin dug. Vposledstvii eto napravlenie issledovanii razvilos' kak gradusnye izmereniya. V VII veke v period rascveta arabskoi civilizacii byli vypolneny gradusnye izmereniya, prichem provodilis' i uglovye i lineinye izmereniya. Uglovye izmereniya oni vypolnyali po nablyudeniyam vysot zvezd v meridiane. U nih odin gradus okazalsya ravnym 111,8 km, a radius Zemli -- 6406 km -- pochti sovremennyi rezul'tat.
Zatem snova nastupil prodolzhitel'nyi pereryv. On svyazan s padeniem arabskoi
civilizacii pod vliyaniem ekspansii mongol'skih plemen i srednevekovoi
sholastiki, kotoraya nadolgo zaderzhala razvitie nauchnoi mysli. Tol'ko v XV
veke v Evrope poyavilsya interes k razmeram nashei planety. On svyazan s
razvitiem torgovyh otnoshenii i kolonizaciei dal'nih zemel'. Neobhodimy byli
tochnye morskie karty. Rodilas' geodeziya. Gollandskii uchenyi Snellius
(1580-1626) predlozhil metod triangulyacii.
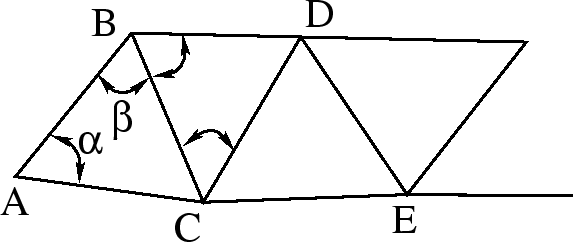
Osnovnaya ideya metoda zaklyuchaetsya v tom, chtoby
s pomosh'yu izmereniya tol'ko odnogo bazisnogo otrezka i izmereniya uglov
poluchit' rasstoyanie do lyuboi drugoi tochki, nahodyasheisya vne bazisa.
Rasstoyanie mezhdu tochkami 
i 
izmeryaetsya s naibol'shei vozmozhnoi tochnost'yu
( ris. 1). Izmeryaya ugly
i
, budem
imet' vse neobhodimye svedeniya dlya opredeleniya treugol'nika
,
sledovatel'no, budem znat' storonu
.
Ee my mozhem schitat' bazisom dlya
sleduyushego treugol'nika
.
Povtoryaya operacii s izmereniem uglov, opredelim
storony novogo treugol'nika. Cepochka, sostoyashaya iz takih treugol'nikov,
mozhet byt' kak ugodno dlinnoi. Ostaetsya opredelit' astronomicheskie
koordinaty tochek, chtoby razvernut' dannuyu triangulyacionnuyu set' na sfere ili
ellipsoide. Etot metod okazalsya ochen' effektivnym i dozhil do nastoyashego
vremeni.
Klassicheskim gradusnym opredeleniem sleduet schitat' rabotu Pikara (Franciya, 1620-1682). Byla opredelena dlina dugi ot Parizha do Am'ena, kotoraya okazalas' ravnoi 153689 m, a v gradusnoi mere -- 1° 23' 55". Takim obrazom, dlina odnogo gradusa sostavila 111212 m. Sovremennoe znachenie dliny dugi odnogo gradusa na shirote Parizha ravno 111221 m, to est' izmereniya Pikara otlichayutsya vsego na 9 m.
V XV111 veke v matematicheskoi stolice mira -- Parizhe vnov' byli organizovany ekspedicii. V ekvatorial'noi zone (Peru) ekspediciya v sostave Buge, Godena i Lakondamina izmerila dlinu dugi meridiana ot 0° 2' 30" severnoi shiroty do 3° 4' 30" yuzhnoi shiroty. Znachenie dliny dugi odnogo gradusa polucheno ravnym 110604 m. V polyarnoi zone (Skandinaviya) rabotala drugaya ekspediciya (Klero, Mopertyui, Kamyuz, Cel'sii). Dlina odnogradusnoi dugi na shirote 66° okazalas' ravnoi 111917 m. Nakonec, neskol'kimi godami ran'she byla izmerena dlina odnogradusnoi dugi pod Parizhem. Ona okazalas' ravnoi 111258 m. Rezul'taty gradusnyh izmerenii v XVIII veke mozhno svesti v sleduyushuyu tablicu
| Shirota, gradusy | Dlina odnogradusnoi dugi, m |
| 1 | 110604 |
| 49 | 111258 |
| 66 | 111917 |
Po etim dannym legko opredelit' i bol'shuyu poluos' obshego zemnogo ellipsoida i ego szhatie.
N'yuton dokazal, chto Zemlya imeet formu ellipsoida vrasheniya so szhatiem 1:230 (sovremennoe znachenie 1:298,25). Etu velichinu on poluchil teoreticheski, prinimaya Zemlyu za odnorodnyi, zhidkii ellipsoid. Sovremennik N'yutona Gyuigens opredelil szhatie zemnogo ellipsoida inache. On predpolozhil, chto sila prityazheniya vsegda napravlena k centru mass Zemli, a ellipsoidal'nost' poverhnosti urovnya sozdaet centrobezhnaya sila, kotoraya otklonyaet otvesnuyu liniyu. Vychisliv szhatie, on poluchil velichinu, ravnuyu 1:576, to est' sushestvenno men'she. Rashozhdenie rezul'tatov N'yutona i Gyuigensa pozzhe ob'yasnil francuzskii matematik Klero, kotoryi poluchil formulu zavisimosti szhatiya ot vnutrennego stroeniya planety. On obobshil teoriyu ravnovesiya planet i pokazal, chto sluchai N'yutona i Gyuigensa yavlyayutsya chastnymi sluchayami ego modeli. Szhatie po Klero ravno
Dlya odnorodnogo ellipsoida s malym szhatiem
. Oboznachim bezrazmernuyu
velichinu, blizkuyu k otnosheniyu centrobezhnoi sily k sile tyazhesti na ekvatore
cherez 
, poluchim
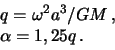
Dlya obshego zemnogo ellipsoida prinyato
Sledovatel'no
Szhatie po N'yutonu v etom sluchae ravno 
= 1:231,12, a po Gyuigensu
= 1:577.80. V nastoyashee vremya General'naya Assambleya MAS v 1976
godu utverdila znachenie szhatiya dlya Zemli = 1:298,2570, kotoroe
lezhit mezhdu dvumya vyshe ukazannymi znacheniyami. Eto oznachaet, chto planeta
Zemlya ne yavlyaetsya odnorodnym ellipsoidom i, odnovremenno, vsya prityagivayushaya
massa ne sosredotochena v centra planety.
Issledovaniya Klero dali nachalo celoi serii rabot takih matematikov kak Puankare, Laplas, Lezhandr, Stoks, Vihert, Darvin i dr. Oni sozdali nauchnoe napravlenie, tesno primykayushee k nashemu predmetu -- teorii figur ravnovesiya nebesnyh tel. Bol'shoi vklad v teoriyu figur nebesnyh tel vnesli Makloren i Yakobi, kotorye issledovali ustoichivost' figur ravnovesiya tel ellipsoidal'noi formy.
Dlya izucheniya formy ekvipotencial'noi poverhnosti s maksimal'noi detal'nost'yu neobhodimo vvesti telo otscheta, otnositel'no kotorogo mozhno vyyavit' eti detali. Dlya Zemli v kachestve tela otscheta berut zemnoi ellipsoid. Togda zadacha opredeleniya figury Zemli svoditsya k vychisleniyu vysot geoida nad etim ellipsoidom. Ishodnym materialom dlya resheniya takoi zadachi sluzhat geodezicheskie i gravimetricheskie svedeniya, poluchennye na poverhnosti Zemli.
Vpervye zadachu opredeleniya figury Zemli postavil i teoreticheski reshil Stoks. Principial'naya vozmozhnost' opredeleniya urovennoi poverhnosti po gravitacionnomu polyu dokazyvaetsya teoremoi Stoksa:
Esli urovennaya poverhnost', celikom ohvatyvayushaya massy, izvestna, izvestny takzhe massa i uglovaya skorost' vrasheniya, to sila tyazhesti odnoznachno opredelyaetsya kak na samoi poverhnosti, tak i vo vsem vneshnem prostranstve.
Simvolicheski eto utverzhdenie mozhno zapisat' tak:
. Nasha
zadacha -- opredelenie figury Zemli -- yavlyaetsya obratnoi: trebuetsya opredelit'
po zadannym 
, 
i 
. Osnovnaya trudnost' resheniya
etoi zadachi svyazana s
opredeleniem na poverhnosti urovnya. Na praktike my mozhem izmeryat' udel'nuyu
silu tyazhesti tol'ko na fizicheskoi poverhnosti. Voznikaet zadacha perenosa
etogo znacheniya (redukcii) s fizicheskoi poverhnosti na geoid (ne na
ellipsoid!).
Nad problemoi redukcii rabotalo mnogo uchenyh. Dominiruyushuyu rol' v etoi teorii sygrali nashi uchenye. Osnovnaya trudnost' zaklyuchalas' v tom, kak "otpravit'" vse massy, lezhashie vyshe poverhnosti geoida, pod etu poverhnost', pri etom ne iskaziv samu poverhnost' urovnya. Eta problema poluchila nazvanie problemy regulyarizacii Zemli. Poslednyuyu tochku v etoi zadache postavil M.S.Molodenskii. On dokazal, chto figuru Zemli mozhno izuchat' i bez regulyarizacii. Dostatochno vse izmereniya vypolnyat' na fizicheskoi poverhnosti, no krome sily tyazhesti neobhodimo znat' i prirashenie potenciala, dlya chego dolzhny byt' vypolneny i geodezicheskie raboty.
Itak, pust' na zemnoi poverhnosti v tochkah s izvestnymi znacheniyami 
i 
budem imet' vektor sily tyazhesti
i gravitacionnyi potencial
. Togda
. Zdes' cherta sverhu oznachaet, chto
sootvetstvuyushie velichiny berutsya na poverhnosti . Esli i odnoznachno
opredelyayut vektor
, to umestno postavit' i obratnuyu zadachu:
opredelit' po zadannym na poverhnosti
i . Pri etom
poverhnost', voobshe govorya, ne yavlyaetsya poverhnost'yu urovnya!
Avstriiskii geodezist G.Moric tak otozvalsya o rabote M.S.Molodenskogo: "Kogda blestyashaya rabota M.S.Molodenskogo stala izvestnoi na zapade, ona proizvela poistine revolyuciyu Kopernika v umah geodezistov vseh stran ..." (G.Moric, "Sovremennaya fizicheskaya geodeziya", Moskva "Nedra" 1983). Eta rabota stimulirovala matematicheskie issledovaniya v oblasti teorii gravitacionnogo potenciala. Na vooruzhenie vzyaty takie ser'eznye matematicheskie discipliny kak teoriya funkcii, teoriya grupp, integral'nye uravneniya, matrichno-tenzornyi analiz i dr. Posledovateli M.S.Molodenskogo sovetskie uchenye L.P.Pellinen, V.V.Brovar, M.Yu.Neiman horosho izvestny v mirovom soobshestve uchenyh.
Poyavlenie sputnikov i novyh vozmozhnostei issledovaniya gravitacionnogo polya
sushestvenno rasshirilo krug zadach teorii figury Zemli. Poyavilos' novoe
napravlenie v vysshei geodezii -- kosmicheskaya geodeziya. Esli ran'she
triangulyaciya razvertyvalas' na fizicheskoi poverhnosti Zemli, to seichas ona
stala trehmernoi. Kosmicheskie triangulyacionnye punkty -- punkty slezheniya za
geodezicheskimi sputnikami. Dvizhenie sputnikov, kak izvestno, opredelyaetsya
kak dvizhenie po nekotoroi orbite vokrug centra mass. Poetomu za nachalo
sistemy otscheta berut centr mass. Krome togo, neobhodimo znat' raspolozhenie
etih punktov otnositel'no tela otscheta, kotorym sluzhit obshii zemnoi
ellipsoid. Vzaimnoe raspolozhenie punktov zadayut geodezicheskimi koordinatami
, sootvetstvenno, shirotoi, dolgotoi i vysotoi. Fundamental'no zadachei
yavlyaetsya opredelenie centra obshego zemnogo ellipsoida otnositel'no centra
mass.
V dosputnikovuyu epohu geodezicheskie raboty vpolne udovletvoryala privyazka k ellipsoidu, approksimiruyushemu issleduemuyu territoriyu. Sovetskii geodezist F.M.Krasovskii poluchil parametry ellipsoida dlya Sovetskogo Soyuza s nachalom otscheta vysot po Kronshtadskomu futshtoku. Szhatie ellipsoida Krasovskogo ravno 1:298,3, Eta velichina znachitel'no otlichalas' ot szhatiya obshego zemnogo ellipsoida prinyatogo v to vremya i poluchennogo po gravimetricheskim dannym. Avtory davali raznye ocenki szhatiya ot 1:296,6 do 1:297,4. Pervoe zhe opredelenie szhatiya po sputnikovym dannym dalo velichinu, prakticheski sovpadayushuyu so szhatiem ellipsoida Krasovskogo. Tochnost' opredeleniya sushestvenno vozrosla. General'naya Assambleya MAS v 1976 g dlya szhatiya Zemli utverdila znachenie 1:298,2570.
Sputnikovye al'timetricheskie issledovaniya dali pryamye izmereniya topografii
vodnoi gladi poverhnosti okeanov, kotoraya sovpadaet s geoidom s tochnost'yu
m. Sami al'timetricheskie nablyudeniya dostigli tochnosti neskol'kih
santimetrov. Poyavilas' neobhodimost' s takoi zhe tochnost'yu stroit' i teoriyu
dvizheniya sputnikov i opredelyat' poverhnost' geoida. Klassicheskoe lineinoe
priblizhenie s tochnost'yu do pervoi stepeni szhatiya stalo nepriemlemym. Esli
radius Zemli raven R, to malymi velichinami my dolzhny schitat' lineinye
velichiny
km. Malymi velichinami vtorogo poryadka budut
m, a tret'ego poryadka --
sm. Otsyuda sleduet, chto teoriya dvizheniya sputnikov dolzhna
obespechivat' santimetrovuyu tochnost', a sovremennaya teoriya figury Zemli
dolzhna stroit'sya tak, chtoby obespechit' tochnost' do malyh tret'ego poryadka. K
sozhaleniyu, takih tochnostei eshe ne polucheno.
<< Titul'nyi list | Oglavlenie | Lekciya 2. Geodezicheskie sistemy koordinat >>
|
Publikacii s klyuchevymi slovami:
gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya
Publikacii so slovami: gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
