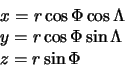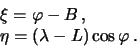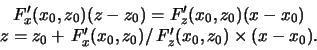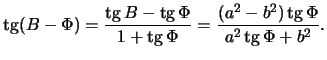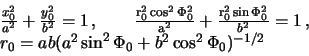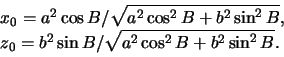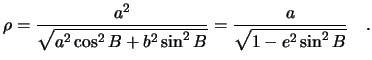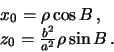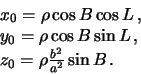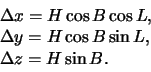<< Lekciya 1. Teoriya figury zemli | Oglavlenie | Lekciya 3. Teoriya potenciala >>
- 2.1 Dekartovy sistemy koordinat
- 2.2 Sfericheskaya sistema koordinat
- 2.3 Geodezicheskaya sistema koordinat
- 2.4 Ellipsoidal'naya sistema koordinat
Lekciya 2. Geodezicheskie sistemy koordinat
Sfericheskaya sistema. Shirota dolgota i radius-vektor. Sistema koordinat, postroennaya na ellipsoide. Geodezicheskie koordinaty: shirota, dolgota i vysota. Svyaz' mezhdu sfericheskoi, geodezicheskoi i dekartovoi sistemami koordinat.
Geodezicheskie zadachi reshayut na ploskosti, esli razmery ploshadi neveliki. Esli issleduemaya chast' poverhnosti zanimaet neskol'ko gradusov shiroty ili dolgoty, to neobhodimo uchityvat' i kriviznu poverhnosti. V etom sluchae chasto podhodit i shar. Dlya resheniya global'nyh zadach, v tom chisle i zadach po kosmicheskoi geodezii v kachestve tela otscheta berut ellipsoid vrasheniya. V chastnosti na ellipsoide reshayut sleduyushie zadachi:
- -- Utochnenie formy i razmerov obshego zemnogo ellipsoida (OZE).
- -- Perenos napravlenii i rasstoyanii s fizicheskoi poverhnosti na ellipsoid.
- -- Opredelenie koordinat tochek na poverhnosti referenc-ellipsoida.
- -- Opredelenie rasstoyanii mezhdu tochkami s zadannymi koordinatami.
- -- Utochnenie koordinat po mere utochneniya elementov ellipsoida.
2.1 Dekartovy sistemy koordinat
Vvedem dve pryamougol'nye sistemy koordinat: lokal'nuyu i global'nuyu.
Nachalo sistemy otscheta (tochka R) dlya lokal'noi pryamougol'noi sistemy
koordinat vyberem v tochke nablyudeniya, lezhashei na poverhnosti ellipsoida. Os'
RH napravim na Sever, os' RU? na Vostok, a os'
po normali k poverhnosti
ellipsoida vniz (po vnutrennei normali). V etoi sisteme koordinat
"gorizontal'naya" ploskost' HRU ne sovpadaet s ploskost'yu astronomicheskogo
gorizonta.
Global'nuyu dekartovu geodezicheskuyu sistemu koordinat Oxyz stroyat tak:
nachalo
otscheta sovmeshayut s centrom OZE (ne putat' s centrom mass Zemli!), ploskost'
xOy -- c ploskost'yu ekvatora. Os' Ox sovmeshayut s liniei peresecheniya ploskosti
nulevogo meridiana i ploskosti ekvatora. Os' Oy peresekaet ekvator v tochke s
dolgotoi 90°. Os' Oz sovpadaet s os'yu vrasheniya OZE.
Eta os' ne obyazatel'no sovpadaet s os'yu vrasheniya Zemli. Dlya trehosnogo
OZE nachalo koordinat berut v centre mass Zemli, a osi -- sovpadayushimi s
glavnymi osyami inercii. V etom sluchae ploskost' xOy, voobshe govorya, ne
budet lezhat' v ploskosti ekvatora.
2.2 Sfericheskaya sistema koordinat
Telom otscheta dlya sfericheskoi sistemy koordinat yavlyaetsya sfera s radiusom
. Nachalo etoi sistemy koordinat sovmeshayut s centrom sfery. Koordinatami
yavlyayutsya geocentricheskaya shirota 
, dolgota 
i radius-vektor 
. Shirotoi
nazyvaetsya ugol mezhdu radiusom-vektorom i ploskost'yu ekvatora. Dolgota est'
ugol mezhdu ploskost'yu, prohodyashei cherez zadannuyu tochku i os'yu vrasheniya
(ploskost' meridiana) i ploskost'yu meridiana, prinyatogo v kachestve nulevogo.
Svyaz' mezhdu sfericheskoi sistemoi i global'noi dekartovoi opredelyaetsya
formulami
V tom sluchae, kogda shirota opredelyaetsya kak ugol mezhdu ploskost'yu ekvatora i
otvesnoi liniei, sfericheskaya sistema koordinat nazyvaetsya astronomicheskoi. Shirota i dolgota, opredelennye
v etoi sisteme my budem oboznachat' cherez 
i 
.
2.3 Geodezicheskaya sistema koordinat
S geodezicheskoi sistemoi koordinat 
svyazyvayut ponyatiya geodezicheskoi
shiroty, dolgoty i vysoty. Geodezicheskaya shirota V est' ugol, pod kotorym
peresekaetsya normal' k poverhnosti ellipsoida s ploskost'yu ekvatora. Dolgota
-- dvugrannyi ugol mezhdu ploskost'yu nulevogo meridiana i ploskost'yu
meridiana, prohodyashego cherez zadannuyu tochku.
Geodezicheskie shirota i dolgota otlichayutsya ot sootvetstvuyushih astronomicheskih koordinat, svyazannyh s otvesnoi liniei, tak kak otvesnaya liniya ne sovpadaet s normal'yu k ellipsoidu. Otklonenie otvesnoi linii mozhno sproecirovat' na dve ploskosti: ploskost' meridiana i ploskost' pervogo vertikala. Netrudno ponyat', chto obe eti sostavlyayushie mozhno opredelit' cherez raznosti mezhdu astronomicheskimi i geodezicheskimi koordinatami
Otkloneniya otvesnoi linii sostavlyayut, kak pravilo, pervye neskol'ko sekund dugi.
Zametim, chto geodezicheskaya i geocentricheskaya dolgoty sovpadayut. Obe oni opredeleny kak dvugrannyi ugol mezhdu ploskost'yu nulevogo meridiana i ploskost'yu, soderzhashei os' vrasheniya i zadannuyu tochku. Geocentricheskaya zhe shirota otlichaetsya ot geodezicheskoi.
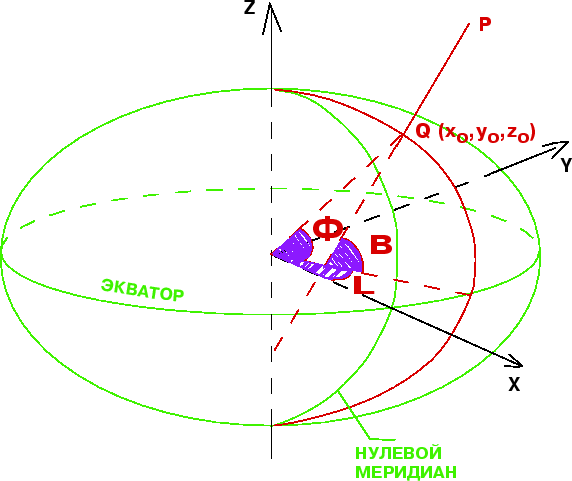
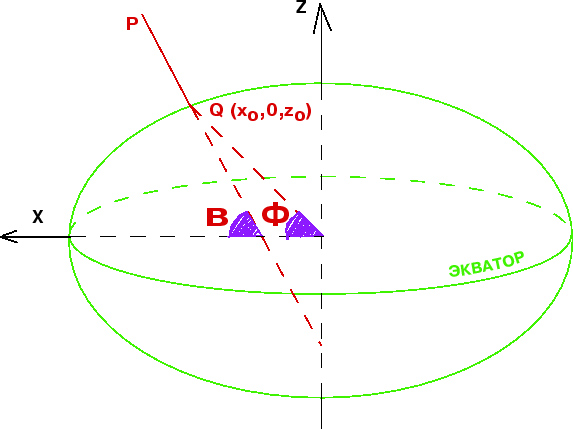
Rassmotrim tochku 
, lezhashuyu vne OZE. Opustim iz etoi tochki perpendikulyar na
poverhnost' ellipsoida i prodolzhim ego do peresecheniya s ekvatorial'noi
ploskost'yu (ris. 2).
Proekciyu tochki na poverhnost' ellipsoida oboznachim cherez
Togda otrezok PQ est' geodezicheskaya vysota tochki .
Ugol, pod kotorym upomyanutyi
perpendikulyar peresekaet ploskost' ekvatora, est' geodezicheskaya shirota 
. Ona
otnositsya kak k tochke 
, tak i k tochke . Geocentricheskie shiroty etih dvuh
tochek, kak vidno iz risunka, razlichayutsya. Geocentricheskaya shirota tochki ugol
mezhdu radius-vektorom etoi tochki i ploskost'yu ekvatora.
Ustanovim svyaz' mezhdu koordinatami tochki , szhatiem ellipsoida 
i
shirotami i . Poskol'ku tochka lezhit na poverhnosti ellipsoida, to ee
pryamougol'nye koordinaty
podchinyayutsya uravneniyu
ellipsoida vrasheniya:
. Rassmotrim sechenie 
.
Togda, kak legko
videt',
. Chtoby
opredelit' 
, nuzhno naiti uglovoi koefficient normali v tochke .
Uravnenie
normali k krivoi 
v tochke
imeet vid
U nas
,
poetomu
,
,
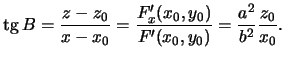
Sledovatel'no,
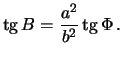
Opredelim otlichie geocentricheskoi shiroty ot geodezicheskoi .
Imeem ochevidnye ravenstva
Vtoroi ekscentrisitet ellipsa, kak my znaem, opredelyaetsya sleduyushim obrazom
, poetomu
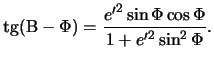
Dlya Zemli vtoroi ekscentrisitet mal, poetomu, prenebregaya malymi vtorogo
poryadka otnositel'no szhatiya, poluchim
. Mozhno
takzhe schitat', chto
Uchityvaya skazannoe, poluchim
Naibol'shee otlichie geodezicheskoi shiroty ot geocentricheskoi dostigaetsya na
shirote 45° i sostavlyaet
.
Svyaz' global'nyh dekartovyh koordinat s geocentricheskimi opredelyaetsya
formulami (2.1). Opredelim teper' formuly, svyazyvayushie dekartovy
koordinaty s
geodezicheskimi. Eto oznachaet, chto by dolzhny opredelit' koordinaty tochki
cherez parametry ellipsoida i geodezicheskie shirotu i dolgotu.
Poskol'ku
, dlya opredeleniya koordinat 
, 
, 
tochki
dostatochno, dlya nachala,
opredelit' tol'ko koordinaty i ,
to est' vse rassuzhdeniya provodit' tol'ko
dlya secheniya . Obratimsya k ris. 3.
Opredelim pryamougol'nye koordinaty tochki , raspolozhennoi na vysote N nad
poverhnost'yu ellipsoida. Snachala opredelim koordinaty proekcii tochki na
poverhnost' ellipsoida (tochka ). Ee koordinaty v sechenii Ohz ravny
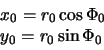
Indeksom "0" my otmetili prinadlezhnost' koordinat k tochke, lezhashei na poverhnosti ellipsoida. Kak my videli
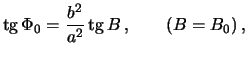
poetomu
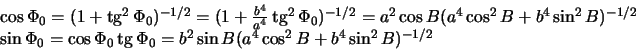
Ostaetsya opredelit' radius-vektor tochki .
Vospol'zuemsya uravneniem ellipsa
i vypolnim neobhodimye preobrazovaniya.
Vyrazim
i
cherez 
i
, dlya chego
vospol'zuemsya privedennymi vyshe formulami. Opredelim radius-vektor tochki
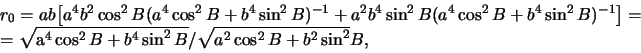
sledovatel'no,
Oboznachim
Teper'
Dlya proizvol'nogo secheniya, prohodyashego cherez os' vrasheniya 
,
budem imet'
Teper' podnimem tochku na vysotu N i sovmestim ee s tochkoi .
Pryamougol'nye koordinaty izmenyatsya na
Okonchatel'no, teper' formuly dlya perescheta geodezicheskih koordinat 
i N v
pryamougol'nye 
primut vid
Zdes' 
, opredelennyi formuloi (2.7) imeet prostoi geometricheskii smysl:
on raven otrezku normali, prohodyashei cherez tochku , ot etoi tochki do tochki
peresecheniya ee s os'yu vrasheniya ellipsoida. Spravedlivost' etogo utverzhdeniya
predlagaetsya dokazat' samostoyatel'no.
2.4 Ellipsoidal'naya sistema koordinat
Rassmotrim eshe odnu sistemu koordinat, imeyushuyu prilozhenie v teorii gravitacionnogo potenciala:
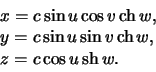
Eti formuly soderzhat ne tri, a chetyre peremennye velichiny. Chetvertaya peremennaya ustanavlivaet semeistvo koordinatnyh poverhnostei -- ellipsoidov. Ubedimsya v etom. Prodelaem prostye preobrazovaniya:
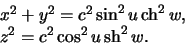
Razdeliv pervoe uravnenie na
a vtoroe -- na
, poluchim
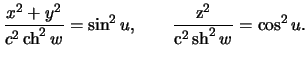
Ochevidno, chto pri
poluchim uravnenie ellipsoida vrasheniya
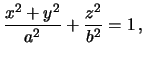
Poskol'ku
,
imeem
, otsyuda
parametr 
imeet prostoi fizicheskii smysl: on raven polovine mezhfokusnogo
rasstoyaniya. Ponyatno, chto izmenyaya 
pri uslovii
,
poluchim semeistvo sofokusnyh
ellipsoidov, igrayushih vazhnuyu rol' v teorii potenciala figur ravnovesiya
Postroim teper' semeistvo koordinatnyh poverhnostei
.
Prodelaem ochevidnye
preobrazovaniya
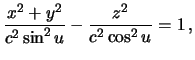
menyaya 
, poluchim semeistvo odnopolostnyh giperboloidov vrasheniya. Oboznachiv
, 
, poluchim uravnenie giperboloida v obsheprinyatoi forme.
Razdeliv u na h, poluchim
. Izmenyaya 
, poluchim semeistvo ploskostei,
prohodyashee cherez os' Oz. Vse
tri semeistva poverhnostei obrazuyut vzaimno ortogonal'nuyu sistemu.
<< Lekciya 1. Teoriya figury zemli | Oglavlenie | Lekciya 3. Teoriya potenciala >>
|
Publikacii s klyuchevymi slovami:
gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya
Publikacii so slovami: gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
