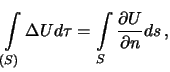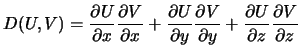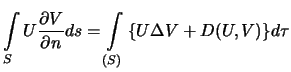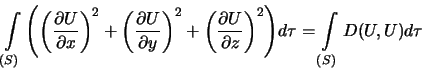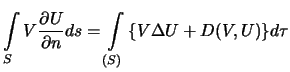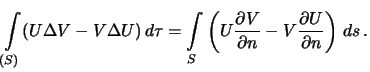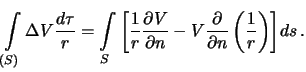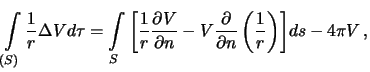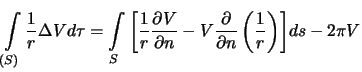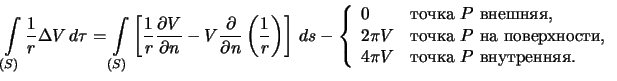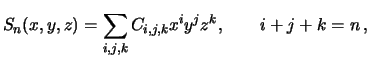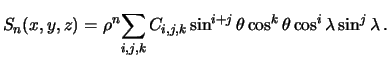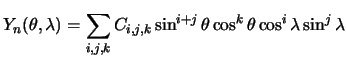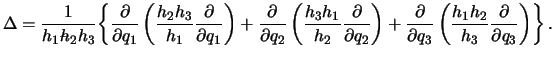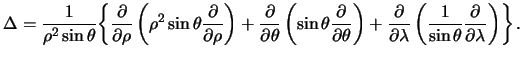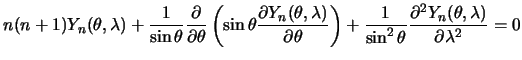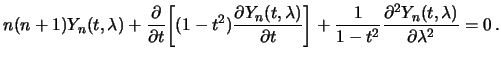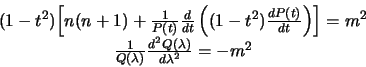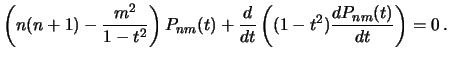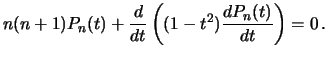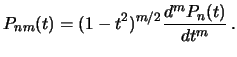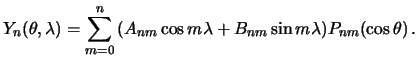<< Lekciya 2. Geodezicheskie sistemy koordinat | Oglavlenie | Lekciya 4. Sfericheskie funkcii >>
Lekciya 3. Osnovnye formuly teorii potenciala
Integral Dirihle, pervaya, vtoraya i tret'ya formuly Grina. Garmonicheskie funkcii i ih svoistva, teoremy o garmonicheskih funkciyah. Sharovye i sfericheskie funkcii. Differencial'noe uravnenie dlya sfericheskih funkcii i ego reshenie.
V dannom razdele perechislim bez vyvoda osnovnye formuly teorii potenciala, kotorye nahodyat primenenie v teorii figury Zemli. Ostanovimsya lish' na nekotoryh, naibolee vazhnyh teoremah.
Vvedem vektornyi operator nabla
![]() :
:
![]() ,
gde
,
gde
![]() -- edinichnye, vzaimno
ortogonal'nye vektora. S vektornym operatorom mozhno obrashat'sya, kak s
obyknovennym vektorom. Naprimer, skalyarnoe proizvedenie dvuh operatorov
nabla daet operator Laplasa:
-- edinichnye, vzaimno
ortogonal'nye vektora. S vektornym operatorom mozhno obrashat'sya, kak s
obyknovennym vektorom. Naprimer, skalyarnoe proizvedenie dvuh operatorov
nabla daet operator Laplasa:
![]() .
.
Dopustim, chto v nashem rasporyazhenii imeetsya nekotoraya skalyarnaya funkciya
![]() . Togda
. Togda
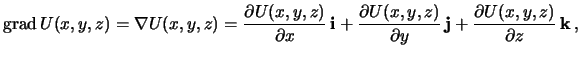
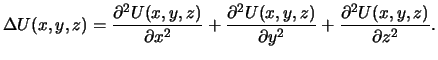
3.1 Formuly Grina
3.1.1 Formula Ostrogradskogo
S pomosh'yu operatora Laplasa integrirovanie po ob'emu mozhno zamenit'
integrirovaniem po poverhnosti. V dal'neishem dlya oboznacheniya predelov
integrirovaniya my budem ispol'zovat' sleduyushii priem. Vse dvukratnye ili
trehkratnye integraly my budem izobrazhat' odnokratnym integralom. Pod
integralom budem ispol'zovat' simvol (![]() ) esli integrirovanie vedetsya po
telu, ogranichennomu poverhnost'yu
) esli integrirovanie vedetsya po
telu, ogranichennomu poverhnost'yu ![]() , ili prosto znachkom
, ili prosto znachkom ![]() , esli
integrirovanie vedetsya po poverhnosti
, esli
integrirovanie vedetsya po poverhnosti ![]() . S etimi gde ogovorkami formula
Ostrogradskogo (3.1) prinimaet vid
. S etimi gde ogovorkami formula
Ostrogradskogo (3.1) prinimaet vid
gde
3.1.2 Pervaya formula Grina
Vvedem oboznachenie operatora
togda pervaya formula Grina primet vid
Integral po ob'emu ot funkcii ![]() nazyvaetsya integralom Dirihle:
nazyvaetsya integralom Dirihle:
Ochevidno, chto v formule Grina funkcii ![]() i
i ![]() mozhno menyat' mestami, to est'
vmesto (3.3) mozhno napisat'
mozhno menyat' mestami, to est'
vmesto (3.3) mozhno napisat'
3.1.3 Vtoraya formula Grina
Vychitaya levye i pravye chasti formul (3.3) i (3.5), poluchim vtoruyu formulu Grina
3.1.4 Tret'ya formula Grina
Rassmotrim chastnyi sluchai, kogda ![]() , gde
, gde ![]() -- rasstoyanie mezhdu dvumya tochkami
P(x,y,z) i
-- rasstoyanie mezhdu dvumya tochkami
P(x,y,z) i
![]() Pervaya tochka imeet fiksirovannye koordinaty, a
vtoraya -- prinadlezhit telu i imeet tekushie koordinaty, prinadlezhashie elementu
ob'ema. Togda
Pervaya tochka imeet fiksirovannye koordinaty, a
vtoraya -- prinadlezhit telu i imeet tekushie koordinaty, prinadlezhashie elementu
ob'ema. Togda
Netrudno ubedit'sya, chto dlya ![]() , imeet mesto ravenstvo
, imeet mesto ravenstvo
![]() .
Imeem
.
Imeem
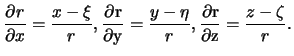
Prodelaem sleduyushie vykladki
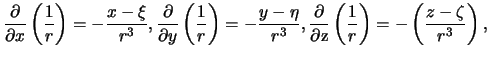
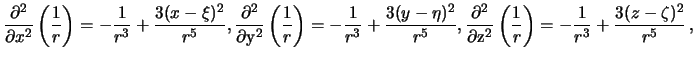
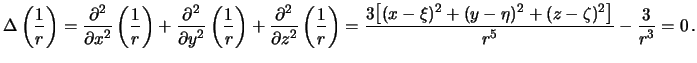
Obratimsya snova k vtoroi formule Grina. Perepishem ee dlya sluchaya, kogda
![]() . Vozmozhny tri varianta, kogda tochka
. Vozmozhny tri varianta, kogda tochka ![]() lezhit vne tela, vnutri ego i na
poverhnosti, kotoroe ogranichivaet eto telo.
lezhit vne tela, vnutri ego i na
poverhnosti, kotoroe ogranichivaet eto telo.
- Tochka R -- vneshnyaya.
V etom sluchae vo vsem vnutrennem prostranstve tela, po kotoromu vedetsya
integrirovanie, radius-vektor r ne obrashaetsya v nul' i
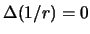 .
Vtoraya formula Grina (3.6) prinimaet vid
.
Vtoraya formula Grina (3.6) prinimaet vid
My poluchili tret'yu formulu Grina dlya vneshnei tochki. - Tochka R -- vnutrennyaya.
V odnoi tochke vnutrennego prostranstva radius-vektor obrashaetsya v nul' i
funkciya
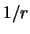 obrashaetsya v beskonechnost'. Opishem vokrug etoi tochki sferu
obrashaetsya v beskonechnost'. Opishem vokrug etoi tochki sferu
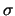 s malym radiusom. Integrirovanie po telu, ogranichennomu
poverhnost'yu
s malym radiusom. Integrirovanie po telu, ogranichennomu
poverhnost'yu 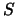 , mozhno razbit' na dva etapa: integrirovaniyu po vsem tochkam
tela, isklyuchaya maluyu sferu, soderzhashuyu tochku
, mozhno razbit' na dva etapa: integrirovaniyu po vsem tochkam
tela, isklyuchaya maluyu sferu, soderzhashuyu tochku 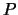 , i integrirovanie po malomu
sharu, ogranichennomu maloi sferoi
, i integrirovanie po malomu
sharu, ogranichennomu maloi sferoi 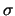 :
gde
:
gde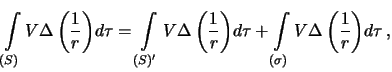
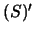 -- telo s vykolotoi tochkoi
-- telo s vykolotoi tochkoi 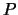 .
Poskol'ku
.
Poskol'ku 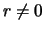 vo vsem vnutrennem prostranstve
vo vsem vnutrennem prostranstve 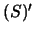 , to
pervoe slagaemoe v pravoi chasti poluchennoi formuly obrashaetsya v nul', tak
kak
, to
pervoe slagaemoe v pravoi chasti poluchennoi formuly obrashaetsya v nul', tak
kak
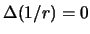 . Zaimemsya vtorym slagaemym. Budem schitat', chto radius
maloi sfery
. Zaimemsya vtorym slagaemym. Budem schitat', chto radius
maloi sfery 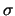 nastol'ko mal, chto funkciyu
nastol'ko mal, chto funkciyu 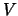 vnutri etoi sfery --
postoyannaya velichina. Togda
vnutri etoi sfery --
postoyannaya velichina. Togda
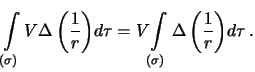
Vospol'zuemsya formuloi Ostrogradskogo, v kotoroi polozhim
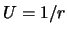 ,
togda vmesto
integrirovaniya po ob'emu budem integrirovat' po poverhnosti maloi sfery
,
togda vmesto
integrirovaniya po ob'emu budem integrirovat' po poverhnosti maloi sfery
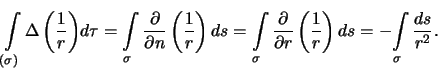
Otnoshenie
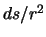 est' elementarnyi telesnyi ugol
est' elementarnyi telesnyi ugol 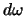 , pod
kotorym "viden" iz tochki
, pod
kotorym "viden" iz tochki 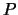 element poverhnosti sfery. Ponyatno, chto, esli
tochka
element poverhnosti sfery. Ponyatno, chto, esli
tochka 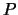 nahoditsya vnutri etoi sfery, to rassmatrivaemyi integral budet raven
polnomu telesnomu uglu, po kotorym vidna poverhnost' sfery iznutri.
Ochevidno, chto on raven
nahoditsya vnutri etoi sfery, to rassmatrivaemyi integral budet raven
polnomu telesnomu uglu, po kotorym vidna poverhnost' sfery iznutri.
Ochevidno, chto on raven 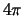 , to est'
, to est'
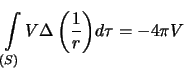
Perepishem formulu (3.6) v sleduyushem vide
V sluchae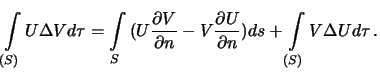
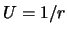 , dlya vneshnei tochki poluchim
, dlya vneshnei tochki poluchim
- Tochka P lezhit na poverhnosti.
Tretii sluchai -- eto kogda tochka
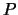 ne yavlyaetsya ni vnutrennei ni vneshnei: ona
lezhit na poverhnosti tela. Mozhno pokazat', chto v etom sluchae
noindent poetomu tret'ya formula Grina prinimaet vid
ne yavlyaetsya ni vnutrennei ni vneshnei: ona
lezhit na poverhnosti tela. Mozhno pokazat', chto v etom sluchae
noindent poetomu tret'ya formula Grina prinimaet vid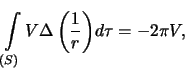
Formuly (3.7), (3.8) i (3.9) mozhno zapisat' odnoi formuloi
3.2 Garmonicheskie funkcii
Garmonicheskoi funkciei koordinat ![]() nazyvaetsya funkciya, nepreryvnaya vmeste so
svoimi pervymi i vtorymi proizvodnymi v nekotoroi oblasti
nazyvaetsya funkciya, nepreryvnaya vmeste so
svoimi pervymi i vtorymi proizvodnymi v nekotoroi oblasti ![]() , udovletvoryayushaya
vo vseh tochkah etoi oblasti uravneniyu Laplasa
, udovletvoryayushaya
vo vseh tochkah etoi oblasti uravneniyu Laplasa
![]() .
.
3.2.1 Svoistva garmonicheskih funkcii
- Lineinaya kombinaciya dvuh i bolee garmonicheskih funkcii est' funkciya
garmonicheskaya.
Pust' U(x,y,z) i V(x,y,z) -- dve garmonicheskie funkcii, to est'
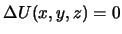 i
i
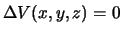 . Voz'mem ih
lineinuyu kombinaciyu
. Voz'mem ih
lineinuyu kombinaciyu
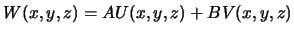 .
Ochevidno, chto
.
Ochevidno, chto
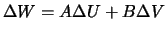 .
Poskol'ku
.
Poskol'ku
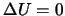 ,
,
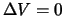 , to i
, to i
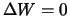 ,
chto i dokazyvaet nashe
utverzhdenie.
,
chto i dokazyvaet nashe
utverzhdenie.
- Esli
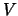 -- garmonicheskaya funkciya, to vse ee chastnye proizvodnye garmonicheskie
funkcii. Dokazatel'stvo osnovano na vzaimnoi perestavimosti operatora
Laplasa
-- garmonicheskaya funkciya, to vse ee chastnye proizvodnye garmonicheskie
funkcii. Dokazatel'stvo osnovano na vzaimnoi perestavimosti operatora
Laplasa 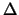 i proizvodnyh. Pust'
togda
i proizvodnyh. Pust'
togda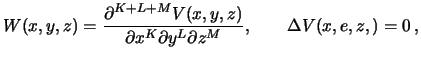
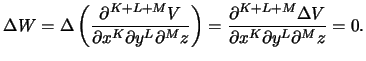
- Lineinoe preobrazovanie koordinat (povorot osei, izmenenie masshtaba) ne
narushaet svoistvo garmonichnosti.
Pust'
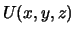 -- garmonicheskaya funkciya. Vvedem novye koordinaty
-- garmonicheskaya funkciya. Vvedem novye koordinaty
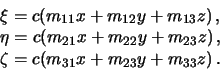
V matrichnom vide privedennoe ravenstvo vyglyadit sleduyushim obrazom
ili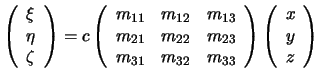
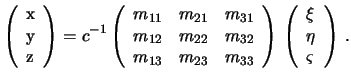
Podstavim v funkciyu
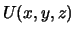 lineinye vyrazheniya dlya
lineinye vyrazheniya dlya
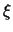 ,
, 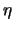 ,
, 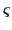 ,
dlya chego vospol'zuemsya vtorym iz privedennyh vyshe ravenstv, poluchim V(
,
dlya chego vospol'zuemsya vtorym iz privedennyh vyshe ravenstv, poluchim V(
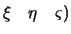 .
Dokazhem, chto esli
.
Dokazhem, chto esli 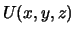 funkciya garmonicheskaya, to i
funkciya garmonicheskaya, to i
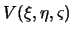 yavlyaetsya garmonicheskoi funkciei.
yavlyaetsya garmonicheskoi funkciei.
Ochevidno, chto
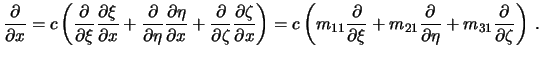
Analogichno
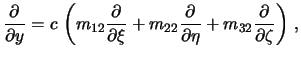
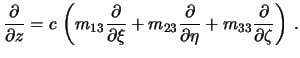
Zapishem poluchennye ravenstva v matrichnoi forme
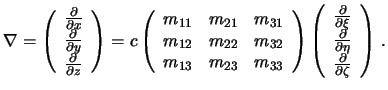
Poskol'ku operator Laplasa est' kvadrat vektornogo operatora nabla
 , to
, to
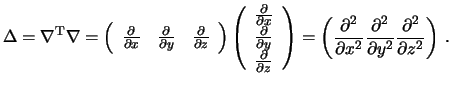
V pravoi chasti budem imet'
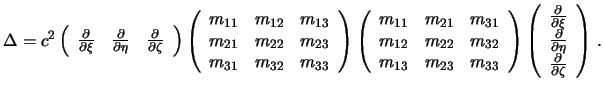
Poskol'ku matricy napravlyayushih kosinusov yavlyayutsya ortonormirovannymi, ih proizvedeniya ravny edinichnoi matrice i operator Laplasa prinimaet vid
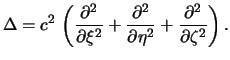
Otsyuda sleduet, chto operator Laplasa yavlyaetsya invariantom po otnosheniyu k povorotu osei, a pri izmenenii masshtaba mnozhitelem s izmenyaetsya na mnozhitel'
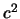 . Drugimi slovami, esli
. Drugimi slovami, esli
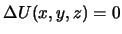 ,
to
,
to
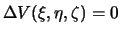 .
.
3.2.2 Teoremy o garmonicheskih funkciyah
- Teorema Gaussa: Potok gradienta garmonicheskoi funkcii cherez zamknutuyu poverhnost' raven nulyu. Potokom nazyvaetsya integral po zadannoi poverhnosti ot
normal'noi proizvodnoi funkcii.
Pust'
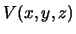 -- garmonicheskaya funkciya. Predpolozhim,
chto zadana zamknutaya poverhnost' S, ogranichivayushaya oblast', vnutri kotoroi
eta funkciya -- garmonicheskaya. Togda, ispol'zuya formulu Ostrogradskogo
(3.1), poluchim
-- garmonicheskaya funkciya. Predpolozhim,
chto zadana zamknutaya poverhnost' S, ogranichivayushaya oblast', vnutri kotoroi
eta funkciya -- garmonicheskaya. Togda, ispol'zuya formulu Ostrogradskogo
(3.1), poluchim
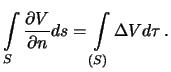
No tak kak funkciya
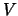 garmonicheskaya, to
garmonicheskaya, to
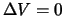 ,
poetomu
,
poetomu
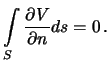
V sluchae, kogda
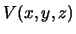 -- potencial prityazheniya,
to spravedlivo uravnenie Puassona
-- potencial prityazheniya,
to spravedlivo uravnenie Puassona
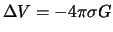 , gde
, gde 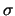 -- plotnost' prityagivayushih mass.
Togda formula (3.1) privodit k formule Gaussa.
-- plotnost' prityagivayushih mass.
Togda formula (3.1) privodit k formule Gaussa.
- Garmonicheskaya funkciya v zamknutoi oblasti D ne imeet
ni minimuma, ni maksimuma.
Prepolozhim obratnoe: vnutri oblasti
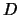 sushestvuet tochka
sushestvuet tochka 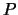 , v kotoroi
garmonicheskaya funkciya imeet maksimum. V maloi okrestnosti etoi tochki na
sfere
, v kotoroi
garmonicheskaya funkciya imeet maksimum. V maloi okrestnosti etoi tochki na
sfere 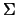 normal'naya proizvodnaya funkcii
normal'naya proizvodnaya funkcii 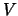 budet otricatel'noi,
togda
budet otricatel'noi,
togda
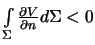 , chto protivorechit teoreme Gaussa.
, chto protivorechit teoreme Gaussa.
- textitPotencial prityazheniya vne prityagivayushih mass ne mozhet
imet' ni minimuma, ni maksimuma; vnutri etoi oblasti mozhet
imet' tol'ko maksimum.
Lyubaya oblast' vne prityagivayushego tela est' oblast' opredeleniya garmonicheskoi funkcii, vnutri kotoroi, soglasno teoreme 2, ne mozhet imet' ni minimuma, ni maksimuma. Predpolozhim obratnoe: vnutri prityagivayushego tela sushestvuet tochka
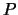 , v kotoroi potencial prityazheniya dostigaet minimuma. V etoi tochke
spravedlivo uravnenie Puassona
, v kotoroi potencial prityazheniya dostigaet minimuma. V etoi tochke
spravedlivo uravnenie Puassona
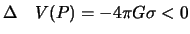 .
Po formule Ostrogradskogo budem imet'
.
Po formule Ostrogradskogo budem imet'
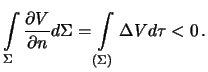
My prishli k protivorechiyu: vsledstvie minimuma vnutri maloi sfery, normal'naya proizvodnaya na poverhnosti etoi sfery budet polozhitel'noi, sledovatel'no i privedennye vyshe integraly budut polozhitel'ny, chto protivorechit sdelannomu vyshe vyvodu. Takim obrazom, teoremu mozhno schitat' dokazannoi.
- Teorema Gaussa.
Znachenie garmonicheskoi funkcii v centre sfery ravno srednemu
iz znachenii etoi funkcii na poverhnosti.
Obratimsya k tret'ei formule Grina, kogda tochka
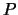 vnutrennyaya. Dlya
garmonicheskoi funkcii
vnutrennyaya. Dlya
garmonicheskoi funkcii
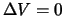 ,
poetomu na sfere
,
poetomu na sfere 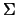 formula (3.8)
prinimaet vid
Na poverhnosti sfery normal'naya proizvodnaya sovpadaet s proizvodnoi po radius-vektoru, poetomu
formula (3.8)
prinimaet vid
Na poverhnosti sfery normal'naya proizvodnaya sovpadaet s proizvodnoi po radius-vektoru, poetomu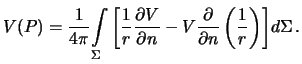 Krome togo, na poverhnosti sfery
Krome togo, na poverhnosti sfery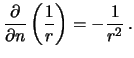
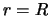 , poetomu
no soglasno teoreme Gaussa o potoke pervoe slagaemoe v poluchennom vyrazhenii ravno nulyu, to est'
, poetomu
no soglasno teoreme Gaussa o potoke pervoe slagaemoe v poluchennom vyrazhenii ravno nulyu, to est'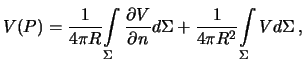 chto i trebovalos' dokazat'.
chto i trebovalos' dokazat'.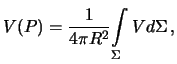
3.3 Sharovye funkcii
Sharovoi funkciei stepeni ![]() nazyvaetsya garmonicheskaya funkciya, yavlyayushayasya
odnorodnym stepennym polinomom vida
nazyvaetsya garmonicheskaya funkciya, yavlyayushayasya
odnorodnym stepennym polinomom vida
gde
gde
Funkciya vida
nazyvaetsya sfericheskoi funkciei.
Itak, sharovaya funkciya stepeni ![]() imeet vid
imeet vid
Sushestvuet i drugoi klass sharovyh funkcii, kotoryi privedem zdes' bez vyvoda
gde
![]() -- ta zhe sfericheskaya funkciya, kotoraya vhodit i
v formulu (3.16).
-- ta zhe sfericheskaya funkciya, kotoraya vhodit i
v formulu (3.16).
Chislo postoyannyh sharovoi funkcii stepeni ![]() ravno
ravno ![]() .
Ubedimsya v etom na pri
mere sharovoi funkcii tret'ei stepeni:
.
Ubedimsya v etom na pri
mere sharovoi funkcii tret'ei stepeni:
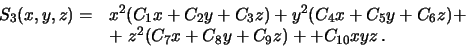
Vsego odnorodnyi polinom tret'ei stepeni imeet 10 postoyannyh. Odnako ne vse postoyannye nezavisimy. Sharovye funkcii podchinyayutsya uravneniyu Laplasa. Vypolniv neobhodimye vykladki, poluchim
Sledovatel'no, iz 10 postoyannyh 3 lineino svyazany uravneniem Laplasa. Ostaetsya 10-3=7 nezavisimyh postoyannyh.
3.3.1 Differencial'noe uravnenie dlya sfericheskih funkcii
Poskol'ku sharovye funkcii udovletvoryayut uravneniyu Laplasa, to est'
Iz differencial'noi geometrii izvestno, chto esli ![]() ,
,
![]() ,
, ![]() -- obobshennye koordinaty, to element dugi v etoi sisteme
koordinat budet imet' vid
-- obobshennye koordinaty, to element dugi v etoi sisteme
koordinat budet imet' vid
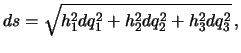
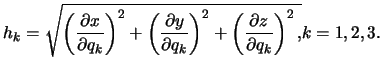
Teper' operator Laplasa mozhno opredelit' sleduyushim obrazom (bez vyvoda)
Opredelim koefficienty Lame dlya sfericheskoi sistemy koordinat. V dannom
sluchae
![]() ,
,
![]() ,
,
![]() , poetomu
, poetomu
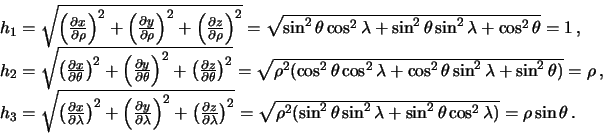
Operator Laplasa dlya sfericheskih koordinat budet vyglyadet' tak
Primenim etot operator k sharovoi funkcii vida
![]() Ochevidno, chto operator Laplasa dlya sharovoi funkcii raven nulyu,
poetomu
Ochevidno, chto operator Laplasa dlya sharovoi funkcii raven nulyu,
poetomu
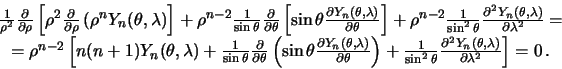
Takim obrazom, differencial'noe uravnenie dlya sfericheskoi funkcii poryadka
![]() imeet vid
imeet vid
Predlagaem samostoyatel'no ubedit'sya v tom, chto
differencial'noe uravnenie dlya funkcii
vhodyashuyu v sharovuyu funkciyu vtorogo roda
![]() sovpadaet s uravneniem (3.20).
sovpadaet s uravneniem (3.20).
3.3.2 Integrirovanie differencial'nogo uravneniya
Zamenim peremennuyu
![]() na
na ![]() . togda
. togda
![]() . Ochevidno, chto
. Ochevidno, chto
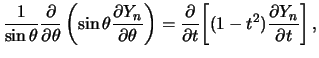
Budem iskat' reshenie etogo uravneniya v vide
![]() . Podstaviv eto vyrazhenie v differencial'noe uravnenie,
budem imet'
. Podstaviv eto vyrazhenie v differencial'noe uravnenie,
budem imet'
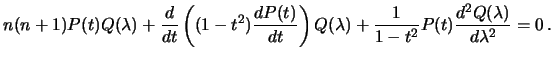
Umnozhiv kazhdyi chlen poluchennogo vyrazheniya na
![]() i podeliv na
i podeliv na
![]() , poluchim
, poluchim
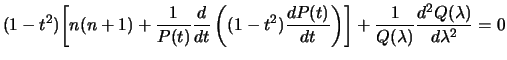
Vidim, chto pervye dva chlena zavisyat tol'ko ot ![]() , a poslednii -- tol'ko ot
, a poslednii -- tol'ko ot
![]() Dlya togo, chtoby uravnenie vypolnyalos' dlya lyubyh
Dlya togo, chtoby uravnenie vypolnyalos' dlya lyubyh ![]() i
i ![]() ,
neobhodimo, chtoby eti funkcii vyrodilis' v konstanty. Naprimer, uravnenie
budet vypolnyat'sya, esli
,
neobhodimo, chtoby eti funkcii vyrodilis' v konstanty. Naprimer, uravnenie
budet vypolnyat'sya, esli
Vtoroe uravnenie est' uravnenie garmonicheskih kolebanii
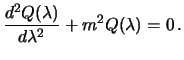
Funkciya
![]() pri celochislennyh znacheniyah
pri celochislennyh znacheniyah ![]() nosit nazvanie
prisoedinennoi (associativnoi) funkcii Lezhandra.
V sluchae
nosit nazvanie
prisoedinennoi (associativnoi) funkcii Lezhandra.
V sluchae ![]() , eti funkcii stanovyatsya stepennymi polinomami, kotorye
nazyvayutsya polinomami Lezhandra.
Polagaya v uravnenii (3.23)
, eti funkcii stanovyatsya stepennymi polinomami, kotorye
nazyvayutsya polinomami Lezhandra.
Polagaya v uravnenii (3.23) ![]() ,
poluchim differencial'noe uravnenie
dlya polinomov Lezhandra
,
poluchim differencial'noe uravnenie
dlya polinomov Lezhandra
V teorii special'nyh funkcii svoistva funkcii i polinomov Lezhandra dostatochno horosho izucheny. Privedem lish' nekotorye svedeniya (bez vyvoda), kotorye mogut prigodit'sya v nashem kurse. Prisoedinennye funkcii Lezhandra i polinomy Lezhandra svyazany mezhdu soboi sootnosheniem
Podvodya itog skazannomu, vypishem okonchatel'nyi vid resheniya differencial'nogo uravneniya dlya sfericheskih funkcii
Zametim, chto poryadok proizvodnoi ![]() v (3.25)
ne mozhet byt' bol'she stepeni
v (3.25)
ne mozhet byt' bol'she stepeni ![]() polinoma Lezhandra.
Po etoi prichine postoyannye
polinoma Lezhandra.
Po etoi prichine postoyannye ![]() i
i ![]() nazyvayut stepen'yu i poryadkom sfericheskih
funkcii.
nazyvayut stepen'yu i poryadkom sfericheskih
funkcii.
<< Lekciya 2. Geodezicheskie sistemy koordinat | Oglavlenie | Lekciya 4. Sfericheskie funkcii >>
|
Publikacii s klyuchevymi slovami:
gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya
Publikacii so slovami: gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |