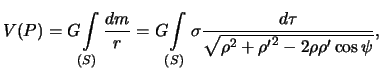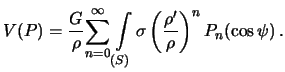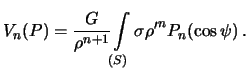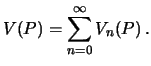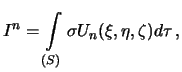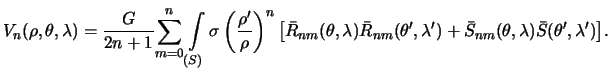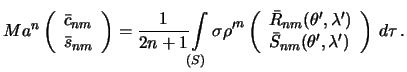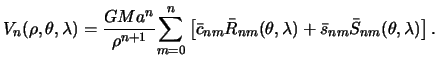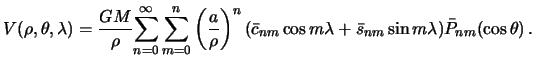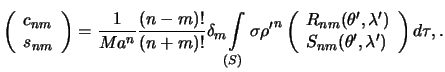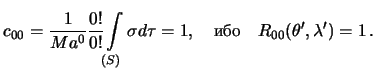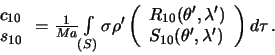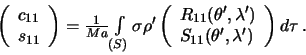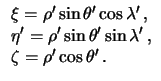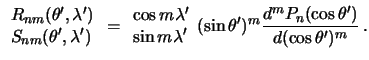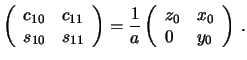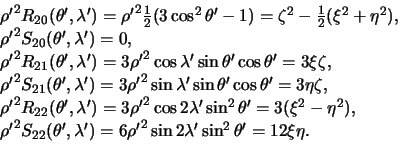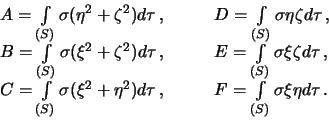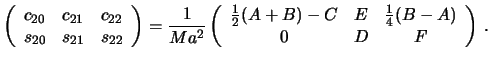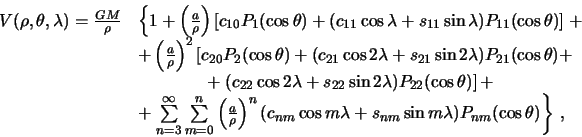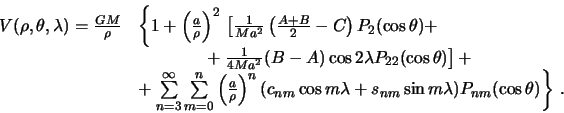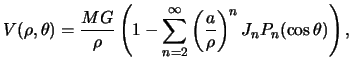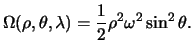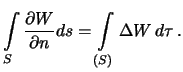---

<< Lekciya 4. Sfericheskie funkcii | Oglavlenie | Lekciya 6. Normal'naya Zemlya >>

Razdely

• 5.1 Razlozhenie gravitacionnogo potenciala v ryad Laplasa
• 5.2 Postochnnye Stoksa
• 5.3 Mehanicheskii smysl stoksovyh postoyannyh
• 5.4 Potencial tyazhesti
• 5.5 Predely Puankare i Krudeli dlya uglovoi skorosti vrasheniya. Figury ravnovesiya

---

Lekciya 5. Analiticheskoe predstavlenie gravitacionnogo potenciala

Proizvodyashaya funkciya polinomov Lezhandra. Razlozhenie potenciala prityazheniya v ryad po sharovym funkciyam. Stoksovy postoyannye. Gravitacionnyi potencial tela vrasheniya. Potencial tyazhesti.

5.1 Razlozhenie gravitacionnogo potenciala v ryad Laplasa

Napomnim, chto pod potencialom kakoi libo sily, v tom chisle i sily tyazhesti my budem ponimat' silovuyu funkciyu. Dlya nachala ostanovimsya na potenciale sil prityazheniya, kotoryi chashe vsego nazyvayut gravitacionnym potencialom. Pust' element massy dm nahoditsya v tochke Q , a tochka P(x,y,z) s fiksirovannymi koordinatami nahoditsya vne prityagivayushego tela. Radius-vektor, soedinyayushii tochki R i Q, budem oboznachat' cherez , a radius-vektory etih tochek sootvetstvenno cherez i . Ugol mezhdu etimi vektorami budem oboznachat' cherez . Esli tochka O -- nachalo koordinat, to iz treugol'nika ORQ sleduet

Potencial prityazheniya tela v tochke imeet vid

gde -- element ob'ema, -- plotnost'. Vynesem iz-pod znaka kornya velichinu , poluchim

Pod znakom integrala stoit proizvodyashaya funkciya polinomov Lezhandra (sm. formulu (4.1)), poetomu

gde -- polinom Lezhandra stepeni .

Teper' potencial prityazheniya v tochke prinimaet vid

Kazhdoe otdel'noe slagaemoe poluchennoi formuly est' funkciya Laplasa dlya potenciala prityazheniya vo vneshnei tochke. Oboznachiv ee cherez , poluchim

Teper' ryad Laplasa mozhno zapisat' tak

Funkcii Laplasa, kak sleduet iz formuly (5.3), zavisyat ot raspredeleniya plotnosti vnutri prityagivayushego tela. Privedennyi integral est' postoyannaya velichina, kotoraya, v svoyu ochered', opredelyaetsya s pomosh'yu tak nazyvaemyh postoyannyh Stoksa, ili, stoksovyh postoyannyh.

5.2 Postochnnye Stoksa

Postoyannoi Stoksa nazyvaetsya velichina, kotoraya opredelyaetsya sleduyushim obrazom

gde garmonicheskaya funkciya vnutri ob'ema integrirovaniya.

Vernemsya k formule (5.3). Vospol'zuemsya formuloi slozheniya garmonicheskih funkcii (4.19). Ee, ochevidno, mozhno perepisat' sleduyushim obrazom

Sledovatel'no

Funkcii tekushih (shtrihovannyh) koordinat i yavlyayutsya garmonicheskimi, tak kak oni prinadlezhat k sharovym funkciyam pervogo tipa. Sledovatel'no, po opredeleniyu (5.5) integraly vida i yavlyayutsya stoksovymi postoyannymi.

Vvedem oboznacheniya

Zdes', kak neskol'ko pozzhe ubedimsya, M -- massa tela, a -- postoyannaya, imeyushaya razmernost' dliny, a i bezrazmernye postoyannye Stoksa.

Teper' funkciyu Laplasa dlya potenciala prityazheniya vo vneshnei tochke

Mozhno predstavit' sleduyushim obrazom

Summiruya po vsem , poluchim iskomoe razlozhenie potenciala prityazheniya v ryad Laplasa

Vse rassuzhdeniya my proveli dlya normirovannyh funkcii, otmechaya ih chertoi sverhu. Odnako eti zhe rassuzhdeniya spravedlivy i dlya nenormirovannyh funkcii. V etom sluchae postoyannye Stoksa budut imet' neskol'ko inoi vid. Opuskaya vykladki, privedem lish' okonchatel'nuyu formulu

gde pri i pri .

5.3 Mehanicheskii smysl stoksovyh postoyannyh

Rassmotrim snachala sluchai, kogda . Togda i , tak kak eta peremennaya izmenyaetsya ot nulya do . Poskol'ku garmonika takzhe ravna nulyu, ostaetsya opredelit' tol'ko . Iz formuly (5.10) sleduet

Rassmotrim teper' sluchai, kogda . Teper' my dolzhny opredelit' chetyre stoksovyh postoyannyh: , , , . Obrashayas' k formule (5.10), poluchim

Dlya togo, chtoby vypolnit' integrirovanie, nuzhno pereiti k dekartovym koordinatam

Po opredeleniyu sfericheskih garmonik imeet mesto ravenstvo

Pri imeem , poetomu

Iz teoreticheskoi mehaniki izvestno, chto koordinaty centra mass tela opredelyayutsya sleduyushim obrazom

poetomu

Itak, sharovaya funkciya pervoi stepeni, kotoruyu predstavlyaet soboi funkciya Laplasa pervoi stepeni, opredelyaet centr mass prityagivayushego tela. Opredelim teper' funkciyu Laplasa vtoroi stepeni. Iz formuly (5.7) sleduet

Snova pereidem k dekartovym koordinatam

Sleduya pravilam teoreticheskoi mehaniki, vypolnim integrirovanie. Budem ispol'zovat' tradicionnye oboznacheniya dlya momentov massy vtorogo poryadka -- momentov inercii

Dlya togo, chtoby privesti formulu dlya koefficientov k okonchatel'nomu vidu, zametim, chto

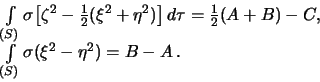
Sledovatel'no, matricu, sostavlennuyu iz koefficientov razlozheniya potenciala prityazheniya dlya sharovoi funkcii vtoroi stepeni, mozhno predstavit' v vide

Vernemsya k formule predstavleniya gravitacionnogo potenciala ryadom Laplasa. Opredelyaya stoksovy postoyannye cherez nenormirovannye sharovye funkcii, formula (5.9) budet imet' tot zhe vid, za isklyucheniem togo, chto stoksovy postoyannye i sfericheskie funkcii "poteryayut" chertu sverhu

gde koefficienty i opredelyayutsya formulami (5.10), (5.16) i (5.19). Poluchennuyu formulu mozhno uprostit', esli prinyat'

1. nachalo koordinat sovpadaet s centrom mass,
2. napravlenie osei sovpadayut s glavnymi osyami inercii.

Pri vypolnenii etih uslovii funkciya Laplasa pervoi stepeni budet ravna nulyu, to est' . Krome togo, budut ravny nulyu i proizvedeniya inercii , , . Sledovatel'no, , a

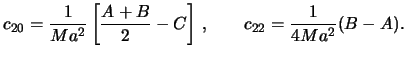
Teper' formula (5.20) prinimaet vid

Poluchennaya formula govorit o tom, chto potencial prityazheniya v tochke zavisit kak ot rasstoyaniya rassmatrivaemoi tochki ot nachala koordinat, tak i sfericheskih koordinat: polyarnogo rasstoyaniya i dolgoty. Odnako otdel'nye sfericheskie garmoniki mogut zaviset' tol'ko ot shiroty, naprimer, pri , v etom sluchae garmoniki nazyvayut zonal'nymi. Poverhnost' sfery v etom sluchae okazyvaetsya razbitoi na zony -- sfericheskie poyasa.

Vtoroi krainii sluchai voznikaet pri . Obratimsya k formule (5.15). V etom sluchae ona priobretaet vid

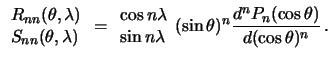
Netrudno ponyat', chto znak sfericheskaya garmonika mozhet menyat' pri opredelennyh znacheniyah dolgoty, tak kak -aya proizvodnaya polinoma -oi stepeni est' postoyannaya velichina, a pri izmenenii polyarnogo rasstoyaniya ot nulya do ne menyaet znaka. Poverhnost' sfery okazyvaetsya razbitoi podobno arbuzu na sektora i sootvetstvuyushie garmoniki, nazyvayutsya sektorial'nymi.

Nakonec, v ostal'nyh sluchayah granicy izmeneniya znaka sfericheskoi garmoniki na poverhnosti sfery obrazuyut mozaiku podobno shahmatnoi doske. Eti garmoniki nazyvayut tesseral'nymi ot latinskogo slova tessera, chto oznachaet sfericheskii chetyrehugol'nik v mozaike.

Dlya mnogih zadach nebesnoi mehaniki silovuyu funkciyu planety approksimiruyut tol'ko zonal'nymi garmonikami. V etom sluchae my predpolagaem, chto rassmatrivaemaya planeta est' telo vrasheniya i zavisimost' sily prityazheniya ot dolgoty tochki, dlya kotoroi beretsya silovaya funkciya, otsutstvuet. Togda gravitacionnyi potencial zapisyvayut v vide

gde Etu postoyannuyu otnosyat k fundamental'nym postoyannym. Esli planeta predstavlyaet soboi telo vrasheniya, to i . Ona zavisit lish' ot momentov inercii, to est' ot momentov mass vtorogo poryadka. Ostal'nye koefficienty nazyvayut mul'tipol'nymi momentami massy. Oni ne imeyut stol' yasnogo mehanicheskogo smysla.

5.4 Potencial tyazhesti

Silovuyu funkciyu udel'noi sily tyazhesti obychno nazyvayut potencialom sily tyazhesti. Pod siloi tyazhesti chasto ponimayut silu, s kotoroi vsyakoe telo prityagivaetsya k Zemle (sm., naprimer, L.V.Sorokin "Gravimetriya i gravimetricheskaya razvedka", Gostoptehizdat, M., 1953). Molchalivo predpolagaetsya, chto eto telo imeet massu, ravnuyu edinice. Poetomu rech' idet ob udel'noi sile tyazhesti. Krome togo, nablyudeniya za deistviem sily provodyatsya vo vrashayusheisya vmeste s Zemlei sisteme koordinat, to est' v neinercial'noi sisteme otscheta. Na probnoe telo, esli net special'nyh ogovorok, deistvuyut lish' dve fizicheskie sily: sila prityazheniya so storony Zemli i uprugaya sila reakcii opory. Rezul'tiruyushaya etih dvuh sil ne ravna nulyu. Summy ih daet kak raz tu silu, kotoraya soobshaet probnomu telu uskorenie, s kotorym telo sovershaet dvizhenie po krugovoi traektorii v processe sutochnogo vrasheniya. Soglasno tret'emu zakonu mehaniki probnoe telo vzaimodeistvuet s oporoi, ono davit na oporu s toi zhe samoi siloi, chto i opora davit na telo. Tyazhest' probnogo tela sozdaet reakciya opory (podstavki). Etu silu nazyvayut vesom tela. Ochevidno, chto ves tela est' sila, ravnaya ravnodeistvuyushei sily prityazheniya i sily inercii, kotoruyu prinyato nazyvat' centrobezhnoi siloi. Itak, udel'naya sila tyazhesti est' ves tela edinichnoi massy, nepodvizhnoi otnositel'no poverhnosti Zemli (ili kakoi-libo drugoi planety). Udel'naya sila imeet razmernost' uskoreniya, poetomu chasto vmesto termina udel'naya sila tyazhesti govoryat uskorenie sily tyazhesti. Na angliiskom yazyke uskorenie sily tyazhesti nazyvayut gravity, na nemeckom -- schwehre, v oboih sluchayah eti slova oboznachayut tyazhest'.

Dlya togo, chtoby zapisat' potencial sily tyazhesti, neobhodimo potencial sily prityazheniya slozhit' s silovoi funkciei dlya centrobezhnoi sily. Etu silovuyu funkciyu v dal'neishem budem nazyvat' potencialom tyazhesti:

gde -- silovaya funkciya dlya centrobezhnoi sily inercii, kotoruyu my uslovno budem nazyvat' centrobezhnym potencialom. Esli os' Oz vybrat' tak, chtoby ona strogo sovpadala s os'yu vrasheniya Zemli, to centrobezhnyi potencial budet imet' vid

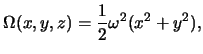
ili v sfericheskih koordinatah

Poverhnost'yu urovnya, to est' poverhnost'yu ravnogo potenciala (ekvipotencial'noi poverhnost'yu) nazyvayut poverhnost', imeyushei uravnenie .

V otlichie ot potenciala prityazheniya potencial tyazhesti ne yavlyaetsya garmonicheskoi funkciei, ibo

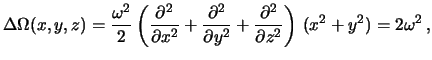
poetomu vne tela, ogranichennogo poverhnost'yu , budet imet' mesto ravenstvo

5.5 Predely Puankare i Krudeli dlya uglovoi skorosti vrasheniya. Figury ravnovesiya

Poverhnost' figury ravnovesiya opredelyaetsya formuloi . Ona sovpadaet s poverhnost'yu urovnya. Potencial tyazhesti na etoi poverhnosti -- postoyannaya velichina. Odnako, dlya togo, chtoby eto telo sushestvovalo, neobhodimo, chtoby sila tyazhesti byla napravlena vnutr' etogo tela. Inymi slovami, normal'naya proizvodnaya potenciala (silovoi funkcii) dolzhna byt' otricatel'na: . Primenim formulu Ostrogradskogo

Vnutri tela potencial prityazheniya ne yavlyaetsya garmonicheskoi funkciei, ibo

. Poetomu . Perepishem formulu (5.25) v vide

gde M -- massa planety, a T -- ee ob'em. Uslovie sohranenie planet, kak tverdogo tela -- polozhitel'noe znachenie sily tyazhesti, poetomu levaya chast' poluchennogo ravenstva otricatel'na. Sledovatel'no . Otsyuda sleduet, chto uglovaya skorost' planety ne mozhet prevoshodit' velichiny , gde -- srednyaya plotnost' planety. Eto est' predel Puankare dlya uglovoi skorosti vrasheniya planety.

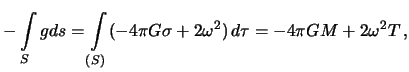
Dlya Zemli , , to est' predel'nyi period vrasheniya dlya Zemli sostavlyaet 4125 s=1,14 chas.

Predel Puankare ne garantiruet ustoichivost' pokoya vseh tel, lezhashih na poverhnosti. Mozhet tak sluchit'sya, chto , no na otdel'nyh uchastkah poverhnosti sila tyazhesti otricatel'na, to est' napravlena vverh! Ustoichivost' pokoya tel budet obespechena, esli poverhnost' urovnya, sovpadayushaya s poverhnost' planety, budet vsegda vypukloi. Dlya etogo usloviya ital'yanskii uchenyi Krudeli dlya odnorodnoi planety snizil predel dlya skorosti vrasheniya v raz: . Period vrasheniya Zemli soglasno predelu Krudeli ne dolzhen byt' men'she 1,61 chasa.

---

<< Lekciya 4. Sfericheskie funkcii | Oglavlenie | Lekciya 6. Normal'naya Zemlya >>

Publikacii s klyuchevymi slovami: gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya Publikacii so slovami: gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya
Sm. takzhe: Sagitovskie chteniya - 2007 Venera: proletaya mimo Sagitovskie chteniya - 2006 K 90-letiyu Nikolaya Panteleimonovicha Grushinskogo Sagitovskie chteniya - 2005 Prosteishaya forma predstavleniya gradienta gravitacionnogo potenciala nebesnyh tel Gora Olimp s orbity Vse publikacii na tu zhe temu >>