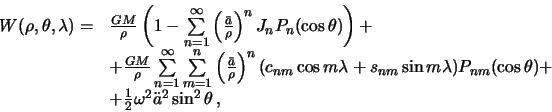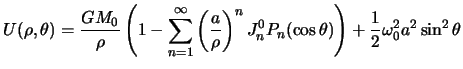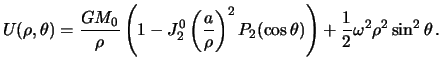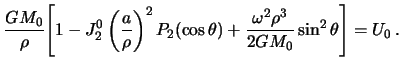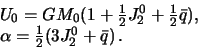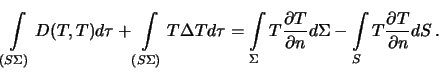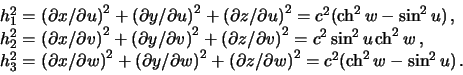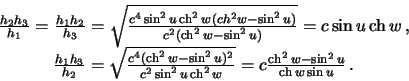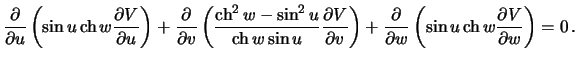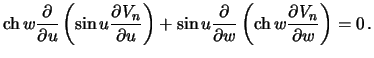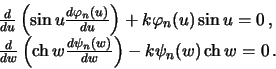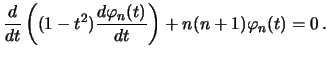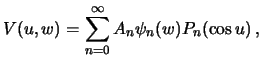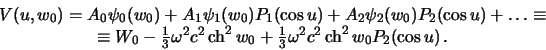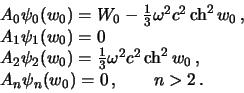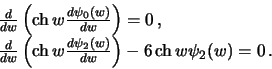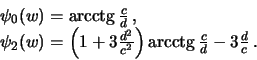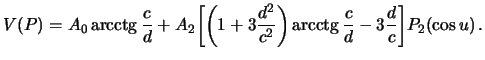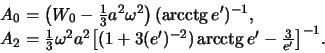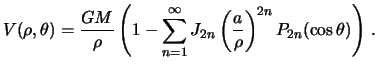---

<< Lekciya 5. Analiticheskoe predst... | Oglavlenie | Lekciya 7. Normal'noe pole tyazhesti >>

Razdely

• 6.1 Normal'nyi potencial tyazhesti
• 6.2 Sferoid Klero
• 6.3 Teorema Stoksa
• 6.4 Gravitacionnyi potencial ellipsoida vrasheniya

---

Lekciya 6. Normal'naya Zemlya

Normal'nyi potencial tyazhesti. Chetyre fundamental'nyh postoyannyh, opredelyayushih potencial tyazhesti. Sferoid Klero. Teorema Stoksa. Gravitacionnyi potencial ellipsoida vrasheniya. Differencial'nye uravneniya, opredelyayushie potencial prityazheniya ellipsoida. Usloviya gidrostaticheskogo ravnovesiya ellipsoida vrasheniya.

Termin normal'naya Zemlya -- tradicionnyi sredi specialistov-geodezistov. Slovo normal'naya primenitel'no k sile tyazhesti, vysote i t.p. oznachaet, chto dannyi parametr yavlyaetsya predskazuemym. Ego mozhno vychislit' po izvestnym formulam. Normal'naya Zemlya -- eto telo otscheta dlya postroeniya kart vysot, glubin morei i t.d. Prichem, eto telo dolzhno opisyvat'sya dostatochno prostymi matematicheskimi formulami i, krome togo, dostatochno horosho approksimirovat' fizicheskuyu poverhnost' planety.

6.1 Normal'nyi potencial tyazhesti

Obshepriznanno, chto naibolee udobnym geometricheskim telom dlya modeli Zemli yavlyaetsya obshezemnoi ellipsoid (OZE) -- urovennyi ellipsoid vrasheniya. Ego gravitacionnyi potencial (potencial tyazhesti!) nazyvayut normal'nym potencialam. Uslovie dlya vybora parametrov normal'noi Zemli:

1. Centr mass i os' vrasheniya normal'noi Zemli sovpadayut sootvetstvenno s centrom mass i os'yu vrasheniya real'noi Zemli.

2. Uglovaya skorost' vrasheniya ellipsoida i real'noi Zemli sovpadayut.

3. Massa ellipsoida ravna masse Zemli.

4. Zonal'nyi koefficient razlozheniya potenciala vtoroi stepeni real'noi Zemli raven sootvetstvuyushemu koefficientu normal'noi Zemli.

Oboznacheniya parametrov normal'noi Zemli my budem otmechat' verhnim ili nizhnim indeksom "0".

Itak, potencial tyazhesti real'noi Zemli imeet vid

gde -- srednii ekvatorial'nyi radius Zemli. Uchityvaya, chto potencial ellipsoida vrasheniya soderzhit tol'ko zonal'nye garmoniki mozhno zapisat'

Uslovie dlya vybora parametrov normal'noi Zemli:

Eti chetyre parametra podlezhat utochneniyu, po mere nakopleniya novyh dannyh. Astronomo-geodezicheskie issledovaniya nuzhdayutsya v edinoi sisteme fundamental'nyh postoyannyh. Takaya sistema obychno ustanavlivaetsya na krupnyh mezhdunarodnyh sobraniyah uchenyh. Na General'noi Assamblee Mezhdunarodnogo Astronomicheskogo Soyuza (MAS) v 1976 g prinyato

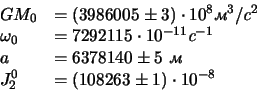
Neskol'ko pozzhe my dokazhem zamechatel'nuyu teoremu Stoksa, kotoraya utverzhdaet, chto, esli izvestna poverhnost' planety, yavlyayushayasya poverhnost'yu urovnya, kotoraya ohvatyvaet vse massy, izvestna takzhe planetocentricheskaya gravitacionnaya postoyannaya i uglovaya skorost' vrasheniya , to gravitacionnoe pole mozhet byt' odnoznachno opredeleno vo vneshnem prostranstve. Chislo parametrov, opredelyayushih ellipsoid vrasheniya ravno dvum (bol'shaya i malaya poluosi). Sledovatel'no vsego nam nuzhno znat' chetyre parametra, ostal'nye opredelyayutsya cherez geocentricheskuyu gravitacionnuyu postoyannuyu, uglovuyu skorost' vrasheniya, bol'shuyu poluos' i szhatie planety. V formulu (6.2) vhodyat beschislennoe mnozhestvo parametrov. Odnako teoriya pokazyvaet, vse stoksovy postoyannye opredelyayutsya cherez uzhe upomyanutye chetyre parametra.

Poskol'ku posledovatel'nost' dlya gidrostaticheski ravnovesnyh figur ubyvaet dostatochno bystro, chasto v formule (6.2) dlya normal'nogo potenciala ogranichivayutsya tol'ko pervym chlenom summy. Togda normal'nyi potencial tyazhesti prinimaet vid

Otbrasyvanie malyh chlenov v razlozhenii potenciala privodit k tomu, chto poverhnost' gde -- postoyannaya velichina, uzhe perestaet, strogo govorya, byt' ellipsoidom. Takuyu poverhnost', blizkuyu k sfere, nazyvayut sferoidom.

Perepishem uravnenie sferoida v sleduyushem vide

Vvedem oboznachenie . Formula (6.4) teper' prinimaet vid

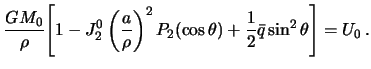
Poskol'ku i -- malye velichiny, uravnenie sferoida mozhno predstavit' tak

gde -- szhatie planety. Prenebregaya velichinami poryadka , uravnenie sferoida (6.4) mozhno uprostit'. Zametim, chto

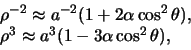
sledovatel'no,

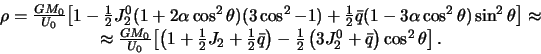
Sravnivaya poluchennoe vyrazhenie s (6.5), poluchim

Takim obrazom, szhatie ravnovesnoi planety zavisit ot stoksovoi postoyannoi i bezrazmernoi uglovoi skorosti vrasheniya , kotoraya imeet prostoi fizicheskii smysl: eto otnoshenie centrobezhnoi sily na ekvatore k velichine, dostatochno blizkoi k sile tyazhesti na ekvatore. Takoi gidrostaticheski ravnovesnyi sferoid nosit nazvanie sferoida Klero, po imeni francuzskogo matematika, rabotavshego nad teoriei ravnovesnyh figur planet.

Szhatie dlya sferoida Klero mozhno zapisat' i tak

gde -- srednee znachenie iz dvuh ekvatorial'nyh momentov inercii. Chetyr'mya fundamental'nymi postoyannymi, v dannom sluchae, yavlyayutsya .

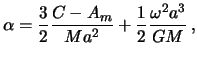
Pri vyvode formuly dlya szhatiya planety my ne pol'zovalis' nikakimi gipotezami o ee stroenii. Klero zhe rassmatrival gidrostaticheski ravnovesnuyu model', polagaya, chto massy raspredeleny v vide tonkih sferoidal'nyh sloev. Im postroena ne tol'ko zavisimost' szhatiya planety ot ee uglovoi skorosti vrasheniya, no i szhatii vnutrennih sloev. Pokazano, chto eti szhatiya umen'shayutsya po mere priblizheniya k centru planety.

Ostaetsya opredelit' zakon izmeneniya sily tyazhesti s shirotoi na sferoide Klero takzhe s tochnost'yu do szhatiya. Iz formuly (6.3) sleduet

Sila tyazhesti na ekvatore

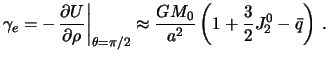
Sila tyazhesti na polyuse

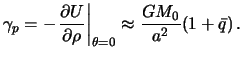
Otnoshenie inogda nazyvayut gravitacionnoe szhatie. Iz privedennyh vyshe formul sleduet

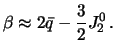
6.2 Sferoid Klero

Eta teorema ustanavlivaet svyaz' geometricheskogo i gravitacionnogo szhatiya s uglovoi skorost'yu vrasheniya planety. Iz privedennyh formul sleduet, chto

Zametim, chto summa geometricheskogo i gravitacionnogo szhatiya v pervom priblizhenii ne zavisit ot vtorogo garmonicheskogo koefficienta , a zavisit lish' ot , i .

6.3 Teorema Stoksa

Eta teorema dokazyvaet edinstvennost' vneshnei kraevoi zadachi teorii potenciala. Drugimi slovami, esli nekotoroe telo ravnomerno vrashaetsya s izvestnoi uglovoi skorost'yu, ego poverhnost', yavlyayushayasya poverhnost'yu urovnya, kotoraya ohvatyvaet vsyu massu, takzhe izvestna, to potencial tyazhesti i ego pervye proizvodnye budut odnoznachno opredeleny kak na poverhnosti , tak i vo vsem vneshnem prostranstve.

Teorema dokazyvaetsya ot protivnogo. Predpolozhim, chto sushestvuet dva razlichnyh potenciala tyazhesti i , kotorye prinimayut na poverhnosti postoyannye znacheniya i . Takim obrazom, , , gde cherta sverhu oznachaet, chto znacheniya funkcii otnosyatsya k poverhnosti . Poskol'ku potencial tyazhesti est' summa potenciala tyagoteniya i centrobezhnogo potenciala, to

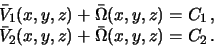
Oboznachim raznost' . Poluchennaya funkciya garmonicheskaya, tak kak potencial prityazheniya -- garmonicheskaya funkciya, udovletvoryayushaya vo vneshnem prostranstve uravneniyu Laplasa.

Primenim pervuyu formulu Grina (sm. lekciyu 3, razdel 3.1.2???) dlya sluchaya, kogda i . Vyberem, v kachestve "tela" po kotoromu nuzhno vypolnit' integrirovanie -- prostranstvo, lezhashee mezhdu poverhnost'yu i sferoi s ochen' bol'shim radiusom, tak chtoby nasha poverhnost' byla celikom vnutri sfery. Oboznachim eto prostranstvo cherez . Teper' pervaya formula Grina budet vyglyadet' sleduyushim obrazom

Znak minus mezhdu integralami v pravoi chasti poluchennoi formuly oznachaet lish' to, chto vneshnyaya normal' dlya odnoi poverhnosti yavlyaetsya vnutrennei dlya drugoi poverhnosti. Rassmotrim poslednii integral. Funkciya na poverhnosti -- postoyannaya velichina, ravnaya , poetomu

Odnako, poskol'ku funkciya T yavlyaetsya garmonicheskoi, integral po zamknutoi poverhnosti ot normal'noi proizvodnoi, soglasno teoreme o potoke (sm. lekciyu 3, razdel 3.2.2), raven nulyu.

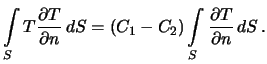
Rassmotrim teper' vtoroi integral v pravoi chasti vyrazheniya (6.7). Proizvodnaya po normali k sfere est' proizvodnaya po radius-vektoru. Poskol'ku dlya ochen' bol'shogo radiusa ishodnoe telo mozhno schitat' material'noi tochkoi, to . Analogichno , gde -- postoyannaya velichina. Otsyuda sleduet

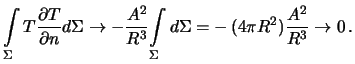
V levoi chasti ravenstva (6.7) nuzhno polozhit' , tak kak -- funkciya garmonicheskaya, poetomu eto vyrazhenie prinimaet vid

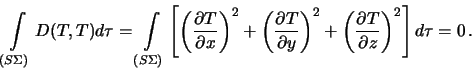
Poskol'ku podyntegral'noe vyrazhenie ne mozhet byt' otricatel'nym ni pri kakih znacheniyah koordinat, ostaetsya sdelat' vyvod, chto -- postoyannaya velichina vo vsem vneshnem prostranstve. No na sfere s beskonechno bol'shim radiusom ona ravna nulyu i v silu nepreryvnosti ona ravna nulyu i na poverhnosti . Takim obrazom T(x,y,z)=0 vo vsem vneshnem prostranstve, to est' , chto i dokazyvaet teoremu.

6.4 Gravitacionnyi potencial ellipsoida vrasheniya

Rassmotrim sluchai, kogda urovennaya poverhnost' est' ellipsoid vrasheniya. Uravnenie etoi poverhnosti v dekartovyh koordinatah imeet vid

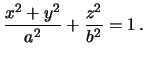
Pereidem k giperbolicheskoi sisteme koordinat (sm. lekciyu 2, razdel 2.4)

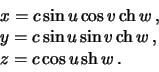
Kak my videli, uravnenie ellipsoida vrasheniya s poluosyami , imeet vid . Dlya opredeleniya potenciala prityazheniya na poverhnosti urovennogo ellipsoida

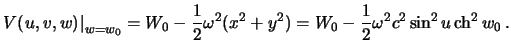
Itak, nam izvesten potencial prityazheniya na poverhnosti ellipsoida. Trebuetsya opredelit' ego vo vsem vneshnem prostranstve. Poskol'ku potencial prityazheniya -- garmonicheskaya funkciya, ona podchinyaetsya differencial'nomu uravneniyu Laplasa, kotoroe mozhno napisat' v vide

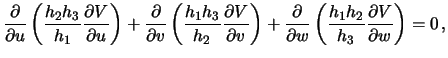
gde -- koefficienty Lame. Opredelim ih

Vychislim otnosheniya koefficientov Lame, stoyashie v differencial'nom uravnenii Laplasa

Itak, uravnenie Laplasa dlya funkcii prinimaet vid

Poluchennoe differencial'noe uravnenie lineino, poetomu budem iskat' reshenie v vide summy garmonicheskih funkcii. V silu osevoi simmetrii ellipsoida vrasheniya i togo, chto granichnye usloviya ne zavisyat ot peremennoi -- analoga dolgoty, to i reshenie uravneniya ne dolzhno soderzhat' etoi peremennoi. Inymi slovami ishem reshenie v vide

gde -- postoyannye, kotorye nuzhno opredelit' iz kraevyh uslovii, a -- garmonicheskie funkcii, udovletvoryayushie uravneniyu Laplasa

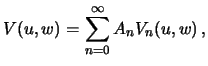
Kak i v sluchae resheniya differencial'nogo uravneniya dlya sfericheskih funkcii, budem iskat' reshenie v vide proizvedeniya dvuh funkcii, kazhdaya iz kotoryh yavlyaetsya funkciei odnoi peremennoi

Podstavim reshenie, zadannoe v vide (6.12) v uravnenie (6.11) i podelim poluchennoe uravnenie na :

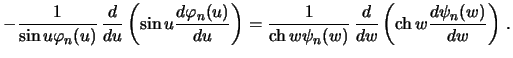
Poluchennoe uravnenie spravedlivo pri lyubyh znacheniyah nezavisimyh peremennyh. Eto vozmozhno lish' v tom sluchae, kogda obe chasti etogo uravneniya ravny odnoi i toi zhe postoyannoi. Oboznachim etu postoyannuyu cherez . Poluchim dva differencial'nyh uravneniya

Pokazhem, chto pervoe iz privedennyh zdes' uravnenii pri est' uravnenie dlya polinomov Lezhandra (sm. lekciyu 3, uravneniya (3.24)-(3.26)), to est'

Polozhim , , togda vmesto pervogo iz uravnenii (6.13) budem imet'

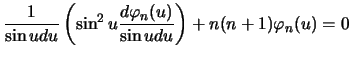
ili

Uravnenie (6.15) sovpadaet s uravneniem dlya polinomov Lezhandra (sm. lekciyu 3, formula (3.24))

Itak, resheniem uravneniya Laplasa v giperbolicheskoi sisteme koordinat budet funkciya

kotoraya na poverhnosti ellipsoida prinimaet znacheniya

Pri vyvode formuly (6.17) my prinyali vo vnimanie, chto . Sravnivaya levuyu i pravuyu chasti formuly (6.17) my prihodim k vyvodu, chto

Itak, v formule (6.16) dlya potenciala prityazheniya ellipsoida otlichnye ot nulya tol'ko koefficienty i , poetomu strogoe vyrazhenie dlya potenciala v giperbolicheskih koordinatah mozhno zapisat' v vide

Ostaetsya opredelit' funkcii i . Kak sleduet iz uravnenii (6.13), funkciyu mozhno opredelit', reshiv vtoroe iz nazvannyh uravnenii pri i pri    :

Poluchennym differencial'nym uravneniyam udovletvoryayut funkcii

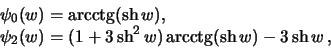
v chem mozhno ubeditsya prostoi podstanovkoi v uravneniya (6.20).

Izbavimsya teper' ot giperbolicheskih funkcii, poluchennyh nami pri reshenii differencial'nyh uravnenii. Kak my uzhe govorili, peremennaya opredelyaet semeistvo sofokusnyh ellipsoidov. Voz'mem nekotoruyu tochku na osi vrasheniya ellipsoida, nahodyashuyusya na rasstoyanii ot centra. Togda dlya etoi tochki , . Zamenim peremennuyu na :

Itak, potencial prityazheniya v proizvol'noi tochke vne ellipsoida imeet vid

Koefficienty i opredelim iz kraevogo usloviya

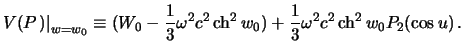
Zametim, chto , , posle sootvetstvuyushih preobrazovanii poluchim

Formuly (6.22) i (6.23) opredelyayut potencial prityazheniya ellipsoidal'nym telom material'noi tochki, lezhashei na poverhnosti sofokusnogo ellipsoida

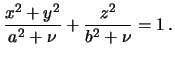
Znaya koordinaty tochki i poluosi ellipsoida i legko opredelit' parametr , a sledovatel'no i maluyu poluos' ellipsoida, prohodyashego cherez zadannuyu tochku.

Iz privedennyh formul vidno, chto potencial prityazheniya soderzhit lish' chetyre nezavisimyh parametra i . Eti chetyre parametra absolyutno strogo opredelyayut potencial prityazheniya ellipsoidal'nym telom material'noi tochki, lezhashei vo veshnem prostranstve, pri lyubom raspredelenii mass vnutri tela lish' by ego poverhnost' ostavalas' poverhnost'yu urovnya.

6.4.1 Svyaz' koefficientov razlozheniya potenciala prityazheniya s chetyr'mya fundamental'nymi postoyannymi

Potencial tela vrasheniya pri osevoi simmetrii raspredeleniya mass mozhet byt' predstavlen v vide razlozheniya po zonal'nym garmonikam. Dopolnitel'noe predpolozhenie o ploskosti ekvatora kak o ploskosti simmetrii privodit k tomu, chto eto razlozhenie budet predstavleno tol'ko chetnymi zonal'nymi garmonikami:

Chetnost' garmonik, vozmozhno, ne ochevidna. No obratimsya k zdravomu smyslu. Esli ellipsoid vrasheniya -- simmetrichnoe otnositel'no ekvatora telo, to i massy ego dolzhny byt' raspredeleny simmetrichno. V protivnom sluchae vozniknet "grushevidnost'", chto privedet k tomu, chto poverhnost' ellipsoida perestanet byt' poverhnost'yu urovnya. Bolee korrektnye rassuzhdeniya provodyatsya s pozicii teorii figur ravnovesiya nebesnyh tel, v kotoroi sushestvovanie ekvatora, kak ploskosti simmetrii, dokazano vpolne strogo.

Formula (6.24) soderzhit beskonechnoe chislo parametrov, hotya ih dolzhno byt' tol'ko chetyre. Otsyuda sleduet, chto koefficienty mozhno vyrazit' cherez drugie fundamental'nye postoyannye.

Ne budem privodit' zdes' dovol'no gromozdkih vykladok, kotorye mozhno naiti v knige L.P.Pellinena "Vysshaya geodeziya" M., Nedra, 1978. Tam pokazano, chto

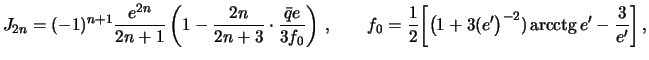
gde i sootvetstvenno pervyi i vtoroi ekscentrisitety ellipsoida. Naprimer,

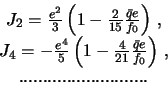
Poskol'ku velichina -- malaya poryadka szhatiya, to koefficienty dlya gidrostaticheski ravnovesnogo ellipsoida ubyvayut s rostom kak stepennaya funkciya ili . Otklonenie ot etogo zakona, kotoroe chasto mozhno nablyudat' na praktike, govorit prezhde vsego o neravnovesnom sostoyanii planety.

---

<< Lekciya 5. Analiticheskoe predst... | Oglavlenie | Lekciya 7. Normal'noe pole tyazhesti >>

Publikacii s klyuchevymi slovami: gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya Publikacii so slovami: gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya
Sm. takzhe: Sagitovskie chteniya - 2007 Venera: proletaya mimo Sagitovskie chteniya - 2006 K 90-letiyu Nikolaya Panteleimonovicha Grushinskogo Sagitovskie chteniya - 2005 Prosteishaya forma predstavleniya gradienta gravitacionnogo potenciala nebesnyh tel Gora Olimp s orbity Vse publikacii na tu zhe temu >>