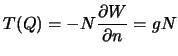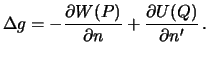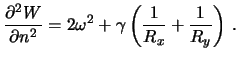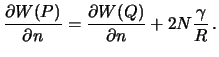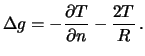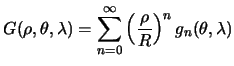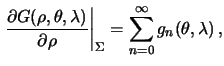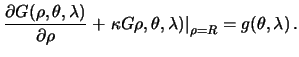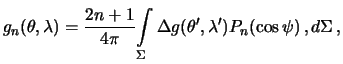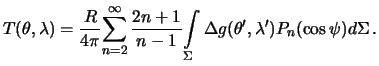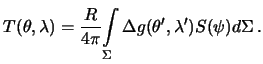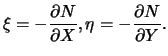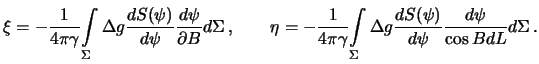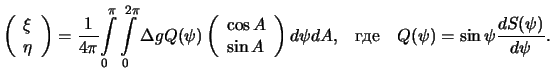<< Lekciya 7. Normal'noe pole tyazhesti | Oglavlenie | Lekciya 9. Kvazigeoid Molodenskogo >>
- 8.1 Vozmushayushii potencial
- 8.2 Kraevaya zadacha Dirihle dlya sfery
- 8.3 Kraevye zadachi Neimana
- 8.4 Smeshannaya kraevaya zadacha
- 8.5 Opredelenie vysot geoida
- 8.6 Opredelenie uklonenii otvesa
Lekciya 8. Opredelenie figury geoida
Vozmushayushii potencial, gravitacionnye anomalii. Kraevoe uslovie dlya vozmushayushego potenciala. Vneshnie i vnutrennie kraevye zadachi Dirihle, Neimana, smeshannye kraevye zadachi. Opredelenie vysot geoida metodom Stokca. Funkciya Stoksa. Opredelenie uklonenii otvesa. Formuly Vening-Meinesa.
8.1 Vozmushayushii potencial
Sredi specialistov po vysei geodezii shiroko primenyaetsya termin vozmushayushii potencial, kak raznost' mezhdu real'nym i normal'nym potencialami v odnoi tochke. Nel'zya skazat', chto termin udachen. V nebesnoi mehanike chasto upotreblyaetsya termin vozmushayushie sily, vozmushayushaya silovaya funkciya, vozmusheniya. Voznikaet vopros, chto imenno vozmushaet dannaya sila? Dlya nebesnoi mehaniki otvet yasen -- zakon dvizheniya tela, delaet ego otlichnym ot keplerovskogo, nevozmushennogo. Pravda, terminologiya moskovskoi i peterburgskoi shkol nebesnyh mehanikov razlichayutsya. Moskvichi govoryat funkciya vozmushayushaya, a peterburzhcy -- perturbacionnaya. Tak chto zhe "vozmushaet" vozmushayushii potencial? Otvet -- nichego. Po-vidimomu prav avstriiskii geodezist G.Moric, kotoryi predlagaet vvesti termin anomaliya potenciala. Govorim zhe my anomaliya sily tyazhesti, imeya v vidu raznost' real'noi i normal'noi sily tyazhesti! No otdavaya dan' tradicii, my budem upotreblyat' termin vozmushayushii potencial imenno kak raznost' real'nogo i normal'nogo potencialov tyazhesti ili prityazheniya vzyatyh v odnoi i toi zhe tochke.
Voz'mem tochku ![]() na poverhnosti geoida
-- urovennoi poverhnosti -- s koordinatami
na poverhnosti geoida
-- urovennoi poverhnosti -- s koordinatami ![]() , gde
, gde ![]() geodezicheskaya vysota tochki (rasstoyanie ot urovennoi
poverhnosti do ellipsoida) Drugimi slovami eto
vysota geoida v tochke
geodezicheskaya vysota tochki (rasstoyanie ot urovennoi
poverhnosti do ellipsoida) Drugimi slovami eto
vysota geoida v tochke ![]() . Dve drugie koordinaty --
. Dve drugie koordinaty -- ![]() i
i ![]() sootvetstvenno
geodezicheskie shirota i dolgota
(sm. lekciyu 2, razdel 2.3).
Na poverhnosti ellipsoida
tochku s takimi zhe znacheniyami shiroty i dolgoty budem oboznachat' bukvoi
sootvetstvenno
geodezicheskie shirota i dolgota
(sm. lekciyu 2, razdel 2.3).
Na poverhnosti ellipsoida
tochku s takimi zhe znacheniyami shiroty i dolgoty budem oboznachat' bukvoi ![]() .
Ponyatno, chto vysota etoi tochki ravna nulyu. Sila tyazhesti v tochke
.
Ponyatno, chto vysota etoi tochki ravna nulyu. Sila tyazhesti v tochke ![]() :
:
Normal'naya sila tyazhesti v tochke ![]() :
:
Raznost' absolyutnyh znachenii etih vektorov opredelyaet smeshannuyu gravitacionnuyu anomaliyu.
Vozmushayushii potencial v tochke ![]() (na ellipsoide) raven
(na ellipsoide) raven
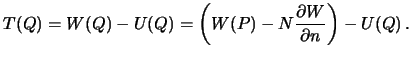
Odnako, poskol'ku
![]() , poluchim
, poluchim
Opredelim smeshannuyu anomaliyu
V pervom slagaemom my differenciruem potencial po vneshnei normali k geoidu,
a vo vtorom -- k ellipsoidu. Eti dva napravleniya, voobshe govorya, ne
sovpadayut. Pravda, otlichie ne veliko i oshibka sostavlyaet vsego
![]() , to est' velichinu poryadka kvadrata otkloneniya
otvesnoi linii. Eto
sushestvenno men'she kvadrata szhatiya, poetomu v nashem priblizhenii mozhno ne
delat' razlichiya v napravleniyah otvesnoi linii i normali k ellipsoidu.
, to est' velichinu poryadka kvadrata otkloneniya
otvesnoi linii. Eto
sushestvenno men'she kvadrata szhatiya, poetomu v nashem priblizhenii mozhno ne
delat' razlichiya v napravleniyah otvesnoi linii i normali k ellipsoidu.
"Opustim" znachenie sily tyazhesti iz tochki ![]() v tochku
v tochku ![]() , primenyaya formuly
lineinogo priblizheniya
, primenyaya formuly
lineinogo priblizheniya
Vertikal'nyi gradient sily tyazhesti, kak my videli (sm. lekciyu 7, uravnenie (7.12)), zavisit ot radiusov krivizny normal'nyh sechenii i uglovoi skorosti vrasheniya Zemli
Prenebregaya malymi poryadka ![]() , mozhno prenebrech' i chlenom
, mozhno prenebrech' i chlenom
![]() . Krome togo, poskol'ku
. Krome togo, poskol'ku ![]() takzhe malaya velichina
(sravneniyu s
takzhe malaya velichina
(sravneniyu s ![]() ), mozhno ne
uchityvat' razlichiya mezhdu radiusami krivizny meridional'nogo secheniya i
secheniya v pervom vertikale. Posle uproshenii, formula (8.3) prinimaet vid
), mozhno ne
uchityvat' razlichiya mezhdu radiusami krivizny meridional'nogo secheniya i
secheniya v pervom vertikale. Posle uproshenii, formula (8.3) prinimaet vid
Teper' smeshannuyu anomaliyu mozhno zapisat' tak
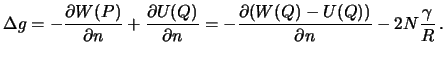
Raznost' ![]() est' vozmushayushii potencial v tochke
est' vozmushayushii potencial v tochke ![]() , a tot, v svoyu
ochered', svyazan s vysotoi geoida
, a tot, v svoyu
ochered', svyazan s vysotoi geoida ![]() formuloi (8.1).
Zamenyaya v etoi formule
real'noe znachenie sily tyazhesti na normal'noe, poluchim
formuloi (8.1).
Zamenyaya v etoi formule
real'noe znachenie sily tyazhesti na normal'noe, poluchim
![]() . Teper'
smeshannuyu anomaliyu mozhno vyrazit' cherez vozmushayushii potencial sleduyushim
obrazom
. Teper'
smeshannuyu anomaliyu mozhno vyrazit' cherez vozmushayushii potencial sleduyushim
obrazom
Itak, zadacha opredeleniya figury geoida (poverhnosti urovnya otnositel'no ellipsoida) svoditsya k opredeleniyu garmonicheskoi funkcii T -- vozmushayushego potenciala, kotoryi lineino svyazan s vysotoi geoida. Problema integrirovaniya uravneniya Laplasa, pri uslovii, chto na zadannoi poverhnosti iskomaya funkciya podchinyaetsya nekotoromu usloviyu, kotoroe nazyvayut kraevym usloviem, prinadlezhit k bol'shomu klassu kraevyh zadach, s nekotorymi iz nih my i poznakomimsya.
8.2 Kraevaya zadacha Dirihle dlya sfery
Popytaemsya reshit' sleduyushuyu zadachu. Dano differencial'noe uravnenie Laplasa,
opredelyayushee funkciyu ![]() , garmonicheskuyu v nekotoroi oblasti, ogranichennoi
zamknutoi poverhnost'yu
, garmonicheskuyu v nekotoroi oblasti, ogranichennoi
zamknutoi poverhnost'yu ![]() . Vse znacheniya etoi funkcii na granice oblasti, to
est' na poverhnosti
. Vse znacheniya etoi funkcii na granice oblasti, to
est' na poverhnosti ![]() , izvestny. Iz vseh reshenii uravneniya Laplasa
trebuetsya vybrat' tol'ko te, kotorye udovletvoryayut kraevomu usloviyu. Reshenie
etoi zadachi sushestvennym obrazom zavisit ot vida granichnoi poverhnosti.
Pokazhem, kak ona reshaetsya, esli zadannaya poverhnost' -- sfera. V dannoi
formulirovke imeem delo s vnutrennei problemoi Dirihle.
, izvestny. Iz vseh reshenii uravneniya Laplasa
trebuetsya vybrat' tol'ko te, kotorye udovletvoryayut kraevomu usloviyu. Reshenie
etoi zadachi sushestvennym obrazom zavisit ot vida granichnoi poverhnosti.
Pokazhem, kak ona reshaetsya, esli zadannaya poverhnost' -- sfera. V dannoi
formulirovke imeem delo s vnutrennei problemoi Dirihle.
Inogda trebuetsya opredelit' garmonicheskuyu funkciyu vne granichnoi poverhnosti. Togda eto vneshnyaya problema Dirihle.
8.2.1 Vnutrennyaya problema Dirihle
Dopustim, chto iskomaya funkciya ![]() zadana na poverhnosti sfery
zadana na poverhnosti sfery ![]() znacheniyami
znacheniyami
![]() . Razlozhim funkciyu
. Razlozhim funkciyu
![]() v ryad Laplasa:
v ryad Laplasa:

| Vnutrennyaya problema Dirihle | Vneshnyaya problema Dirihle |
| Iskomym resheniem budet | Reshenie uravneniya Laplasa zadayut v vide summy sharovyh funkcii vtorogo roda |
|
|
|
tak kak:
|
Eta funkciya takzhe:
|
8.3 Kraevye zadachi Neimana
Na poverhnosti inogda zadany ne znacheniya funkcii, a ee normal'nye proizvodnye. Togda eto zadacha Neimana, kotoraya takzhe mozhet byt' i vnutrennei i vneshnei.
Kraevoe uslovie v etom sluchae imeet vid

gde
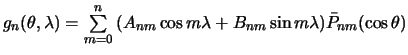 -- funkciya Laplasa.
-- funkciya Laplasa.
Poskol'ku
![]() , dlya vypolneniya teoremy Gaussa dlya
garmonicheskih funkcii o potoke neobhodimo, chtoby vypolnyalos' uslovie
, dlya vypolneniya teoremy Gaussa dlya
garmonicheskih funkcii o potoke neobhodimo, chtoby vypolnyalos' uslovie
![]() , chto ekvivalentno usloviyu
, chto ekvivalentno usloviyu
![]() .
.
| Vnutrennyaya problema Neimana | Vneshnyaya problema Neimana |
| Netrudno ubedit'sya, chto resheniem vnutrennei problemy Neimana budet | Etu problemu na sfere reshaet funkciya |
|
|
|
| Deistvitel'no, eta funkciya garmonicheskaya, tak kak sostoit iz summy sharovyh funkcii pervogo roda, a podstanovka ee v kraevoe uslovie (8.9) ubezhdaet nas, chto ono vypolnyaetsya. | V spravedlivosti etogo utverzhdeniya predlagaem ubedit' samostoyatel'no. |
8.4 Smeshannaya kraevaya zadacha
Eta zadacha, kak i dve predydushie mozhet byt' i vnutrennyaya, i vneshnyaya. Rassmotrim variant vneshnei smeshannoi kraevoi zadachi, imeyushei otnoshenie k teorii figury Zemli. Kraevym usloviem v etom sluchae budet lineinaya kombinaciya samoi iskomoi funkcii i ee normal'noi proizvodnoi na granichnoi poverhnosti
Snova reshenie budem iskat' v vide razlozheniya po sfericheskim funkciyam
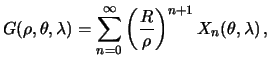

Priravnivaya sfericheskie funkcii odinakovyh stepenei pochlenno, poluchim

Sledovatel'no, resheniem vneshnei smeshannoi kraevoi zadachi budet
8.5 Opredelenie vysot geoida
My ubedilis' v tom, chto vozmushayushii potencial yavlyaetsya garmonicheskoi funkciei i na sfere vypolnyaetsya kraevoi uslovie (8.6). Eto tipichnaya vneshnyaya smeshannaya kraevaya zadacha. Chtoby ee reshit', nuzhno predstavit' smeshannuyu gravitacionnuyu anomaliyu ryadom Laplasa
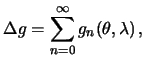
gde
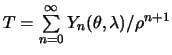 ,
gde
,
gde
V klassicheskom reshenii dannoi zadachi, poluchivshei nazvanie zadachi Stoksa,
predpolagaetsya, chto massa ellipsoida ravna masse real'noi Zemli, to est'
![]() , a nachalo koordinat sovpadaet s centrom mass planety
, a nachalo koordinat sovpadaet s centrom mass planety
![]() Otsyuda sleduet, chto razlozhenie vozmushayushego potenciala
nachinaetsya s
Otsyuda sleduet, chto razlozhenie vozmushayushego potenciala
nachinaetsya s ![]() :
:

Prenebregaya kvadratom szhatiya, my snova differencirovanie po normali zamenim differencirovaniem po radius-vektoru
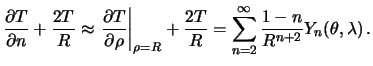
Sledovatel'no
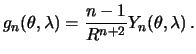
Zametim, chto pri ![]() , dolzhno byt'
, dolzhno byt'
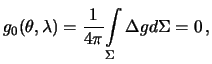
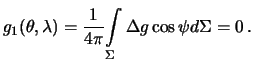
Podstavim syuda integral'nuyu formu (8.14) dlya funkcii Laplasa:
Poskol'ku integrirovanie vedetsya po sfere radiusa ![]() v formule (8.16) my
polagali
v formule (8.16) my
polagali ![]() . Vvedem oboznachenie
. Vvedem oboznachenie
i reshenie zadachi Stoksa prinimaet okonchatel'nyi vid
Funkciyu ![]() chasto nazyvayut funkciei Stoksa.
V (8.17) ona zadana v vide
razlozheniya po stepenyam polinomov Lezhandra ot kosinusa central'nogo
rasstoyaniya
chasto nazyvayut funkciei Stoksa.
V (8.17) ona zadana v vide
razlozheniya po stepenyam polinomov Lezhandra ot kosinusa central'nogo
rasstoyaniya ![]() . Ee "kompaktnyi" vid sleduyushii
. Ee "kompaktnyi" vid sleduyushii
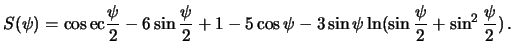
Legko videt', chto tochka ![]() -- osobaya. Zdes' funkciya Stoksa obrashaetsya v
beskonechnost', tem ne menee integral
(8.18) shoditsya, no pri vypolnenii dvuh
ukazannyh vyshe uslovii, kotorym dolzhny udovletvoryat' gravitacionnye
anomalii. Ispol'zuya formulu (8.1),
kotoruyu chasto nazyvayut formuloi Brunsa,
iz vozmushayushego potenciala legko poluchit' vysoty geoida
-- osobaya. Zdes' funkciya Stoksa obrashaetsya v
beskonechnost', tem ne menee integral
(8.18) shoditsya, no pri vypolnenii dvuh
ukazannyh vyshe uslovii, kotorym dolzhny udovletvoryat' gravitacionnye
anomalii. Ispol'zuya formulu (8.1),
kotoruyu chasto nazyvayut formuloi Brunsa,
iz vozmushayushego potenciala legko poluchit' vysoty geoida
8.6 Opredelenie uklonenii otvesa
Otvesnaya liniya (vertikal') sovpadaet s napravlenie vektora sily tyazhesti g.
Ona yavlyaetsya normal'yu k urovennoi poverhnosti. S drugoi storony normal' k ellipsoidu sovpadaet s napravleniem vektora normal'noi sily tyazhesti. Eti dve normali ne sovpadayut. Mezhdu nimi obrazuetsya ugol, kotoryi geodezisty nazyvayut ukloneniem otvesa. Ne budet oshibkoi skazat' i otklonenie otvesnoi linii. Pravda voznikaet vopros otklonenie ot chego? Chtoby takih voprosov ne voznikalo, my budem upotreblyat' geodezicheskii termin.
Dve upomyanutye normali, prodolzhennye vverh, peresekayutsya s voobrazhaemoi nebesnoi sferoi v tochkah, odna iz kotoryh budet astronomicheskim zenitom (ili prosto zenitom), a drugaya -- geodezicheskim. Ponyatno, chto i ploskosti gorizonta astronomicheskogo i geodezicheskogo ne sovpadayut. Dogovorilis' schitat' ukloneniya otvesa polozhitel'nym, esli zenit smeshaetsya v severnom ili vostochnom napravlenii.
Obratimsya k lokal'noi geodezicheskoi sisteme koordinat s nachalom v punkte
nablyudenii (tochka ![]() ). Gorizontal'nye osi PX i PY,
kak my znaem iz lekcii 7, lezhat
v ploskosti, perpendikulyarnoi k normali k ellipsoidu. Odna iz nih napravlena
na sever, drugaya -- na vostok. Os' PZ napravlena vniz po vnutrennei normali k
ellipsoidu. Netrudno ponyat', chto pri polozhitel'nyh "gorizontal'nyh"
komponentah vektora sily tyazhesti obe komponenty ukloneniya otvesa budut
otricatel'ny. Poetomu komponenty ukloneniya otvesa v ploskosti meridiana i
pervogo vertikala sootvetstvenno opredelyayut sleduyushim obrazom
). Gorizontal'nye osi PX i PY,
kak my znaem iz lekcii 7, lezhat
v ploskosti, perpendikulyarnoi k normali k ellipsoidu. Odna iz nih napravlena
na sever, drugaya -- na vostok. Os' PZ napravlena vniz po vnutrennei normali k
ellipsoidu. Netrudno ponyat', chto pri polozhitel'nyh "gorizontal'nyh"
komponentah vektora sily tyazhesti obe komponenty ukloneniya otvesa budut
otricatel'ny. Poetomu komponenty ukloneniya otvesa v ploskosti meridiana i
pervogo vertikala sootvetstvenno opredelyayut sleduyushim obrazom
Iz privedennyh formul vidno, chto obe komponenty -- bezrazmernye velichiny, hotya na praktike oni izmeryayutsya v uglovyh edinicah. Delo v tom, chto ukloneniya otvesa na Zemle sostavlyayut sekundy dugi, poetomu vmesto trigonometricheskih formul, svyazyvayushih ukloneniya otvesa s komponentami vektora sily tyazhesti, my vzyali prostoe otnoshenie.
S drugoi storony

poetomu
Ranee my videli, chto
![]() , poetomu
, poetomu
Formula (8.19) pozvolyaet vychislit' vysoty geoida,
esli na poverhnosti Zemli
zadany smeshannye gravitacionnye anomalii.
Principial'no ne imeet znacheniya, v
kakih koordinatah zadany eti anomalii i v kakih koordinatah prakticheski
vedetsya integrirovanie. My dlya etih celei budem primenyat' geodezicheskie
koordinaty ![]() i
i ![]() . Perepishem formulu (8.19)
. Perepishem formulu (8.19)

Integrirovanie budem vypolnyat' na sfere, a ne na ellipsoide. Pri etom mozhno ozhidat' pogreshnost' v opredelenii vysot geoida poryadka szhatiya. Prenebregaya etimi pogreshnostyami, opredelim elementarnye prirasheniya dlya osei PX i PY

Teper' nuzhno vychislit' proizvodnye
![]() i
i
![]() . Dlya etogo obratimsya k formulam
sfericheskoi trigonometrii.
. Dlya etogo obratimsya k formulam
sfericheskoi trigonometrii.
Rassmotrim sfericheskii treugol'nik, kotoryi obrazuyut dugi, soedinyayushie tri
tochki na sfere: tochku ![]() , v kotoroi my hotim opredelit'
uklonenie otvesa, tochku
, v kotoroi my hotim opredelit'
uklonenie otvesa, tochku
![]() -- polyus, i tochku
-- polyus, i tochku ![]() -- tekushuyu tochku na
poverhnosti sfery, gde raspolozhen
element poverhnosti. Duga PN ravna 90-
-- tekushuyu tochku na
poverhnosti sfery, gde raspolozhen
element poverhnosti. Duga PN ravna 90-![]() ,
a duga QN ravna 90-
,
a duga QN ravna 90-![]() . Ugol pri
tochke
. Ugol pri
tochke ![]() raven
raven ![]() -- azimutu tekushei tochki
-- azimutu tekushei tochki ![]() Duga
RR' ravna argumentu funkcii Stoksa --
Duga
RR' ravna argumentu funkcii Stoksa --
![]() . Ugol pri polyuse
. Ugol pri polyuse ![]() raven raznosti dolgot tochki
raven raznosti dolgot tochki ![]() i tochki
i tochki ![]() , to est'
, to est' ![]() . Ispol'zuya
formuly sfericheskoi trigonometrii, neslozhno poluchit' proizvodnye ugla
. Ispol'zuya
formuly sfericheskoi trigonometrii, neslozhno poluchit' proizvodnye ugla
![]() po
po ![]() i po
i po ![]() , vhodyashie v formuly (8.23)
, vhodyashie v formuly (8.23)
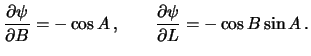
Podstavim poluchennye vyrazheniya v (8.23), poluchim
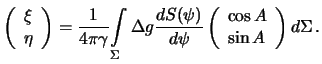
Zapishem privedennyi integral v vide dvukratnogo integrala. Element sfery
raven
![]() ,
prichem peremennaya
,
prichem peremennaya ![]() izmenyaetsya ot 0 do
izmenyaetsya ot 0 do
![]() , a peremennaya
, a peremennaya ![]() -- ot 0 do
-- ot 0 do ![]() . Poluchim
. Poluchim
Eti formuly nosyat imya gollandskogo uchenogo Vening-Meinesa. Kak i v formulu
Stoksa, opredelyayushei vysotu geoida tochka ![]() yavlyaetsya ustranimoi osoboi
tochkoi.
yavlyaetsya ustranimoi osoboi
tochkoi.
Na praktike ispol'zuyut bolee slozhnye metodiki dlya vychisleniya uklonenii otvesa s ispol'zovaniem i gravimetricheskih i geodezicheskih dannyh.
<< Lekciya 7. Normal'noe pole tyazhesti | Oglavlenie | Lekciya 9. Kvazigeoid Molodenskogo >>
|
Publikacii s klyuchevymi slovami:
gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya
Publikacii so slovami: gravimetriya - potencial - gravitacionnoe pole - figura Zemli - geodeziya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |