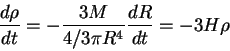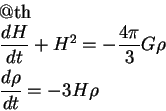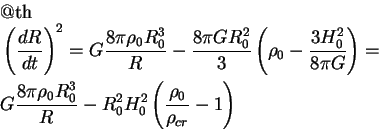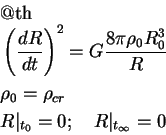<< 10. Kosmologiya | Oglavlenie | 10.2 Modeli Fridmana s >>
- 10.1.1 Kosmologicheskii princip
- 10.1.2 "Kratkii kurs" istorii kosmologii HH veka
- 10.1.3 Zakon Habbla
- 10.1.4 Zakon evolyucii. Kriticheskaya plotnost'
- 10.1.5 Vliyanie davleniya
10.1 Fridmanovskaya kosmologiya
V etom razdele rassmotrim odnorodnye i izotropnye kosmologicheskie modeli Vsedennoi, vpervye rassmotrennye A.A. Fridmanom v 1922 g. i nosyashie ego imya.
10.1.1 Kosmologicheskii princip
Podobno principu potoyanstva skorosti sveta ili principu ekvivalentnosti (kotorye lezhat v osnove obshei teorii otnositel'nosti), v osnove sovremennyh kosmologicheskih modelei lezhit kosmologicheskii princip, soglasno kotoromu vo Vselennoi ne dolzhno byt' vydelennyh nablyudatelei. Inogda etot princip nazyvayut "principom Kopernika", kotoryi pervyi v novoi istorii otkazalsya ot geocentricheskoi sistemy mira. Etot princip oznachaet, chto global'nye harakteristiki Vselennoi odinakovy dlya lyubogo nablyudatelya, nahodyashegosya v lyuboi tochke giperpoverhnosti postoyannogo vremeni.
V nastoyashee vremya etot princip s ogromnoi tochnost'yu
podtverzhden astronomicheskimi nablyudeniyami
odnorodnosti raspredeleniya materii vo Vselennoi
v bol'shih masshtabah
(![]() Mpk) i izotropii (otsutstvie vydelennogo
napravleniya na urovne flyuktuacii temperatury reliktovogo fona
Mpk) i izotropii (otsutstvie vydelennogo
napravleniya na urovne flyuktuacii temperatury reliktovogo fona
![]() ). Uzhe odnogo etogo okazyvaetsya dostatochnym,
chtoby iz vsego myslimogo mnogoobraziya vozmozhnyh matematicheskih modelei,
opisyvayushih Vselennuyu v celom, vybrat' ves'ma uzkii klass odnorodnyh
izotropnyh prostranstv (t.n.
modeli Fridmana-Robertsona-Uokera). Sm. podrobnee v neprevzoidennoi
monografii S.Veinberga
"Gravitaciya i kosmologiya", M.: Mir, 1975, Gl. 13 i dalee).
). Uzhe odnogo etogo okazyvaetsya dostatochnym,
chtoby iz vsego myslimogo mnogoobraziya vozmozhnyh matematicheskih modelei,
opisyvayushih Vselennuyu v celom, vybrat' ves'ma uzkii klass odnorodnyh
izotropnyh prostranstv (t.n.
modeli Fridmana-Robertsona-Uokera). Sm. podrobnee v neprevzoidennoi
monografii S.Veinberga
"Gravitaciya i kosmologiya", M.: Mir, 1975, Gl. 13 i dalee).
10.1.2 "Kratkii kurs" istorii kosmologii HH veka
Ochen' shematichno noveishuyu istoriyu sovremennoi
kosmologii mozhno prosledit' po datam vazhneishih nablyudatel'nyh
i teoreticheskih otkrytii:
1910-1922, V. Slaifer, krasnye smesheniya v spektrah galaktik
gde
1916, A. Einshtein, Obshaya teoriya otnositel'nosti
1922-24, A. Fridman, nestacionarnye resheniya uravnenii
Einshteina (fridmanovskie kosmologicheskie modeli)
1929, E. Habbl, zakon ![]() dlya udalyayushihsya galaktik.
Skorost' udaleniya galaktiki opredelyaetsya po krasnomu smesheniyu,
interpretiruya ego effektom Dopplera. Dlya malyh
dlya udalyayushihsya galaktik.
Skorost' udaleniya galaktiki opredelyaetsya po krasnomu smesheniyu,
interpretiruya ego effektom Dopplera. Dlya malyh ![]()
Pervoe izmerenie postoyannoi Habbla (sm. primer sovremennoi Habblovskoi diagrammy na Ris. 10.1)
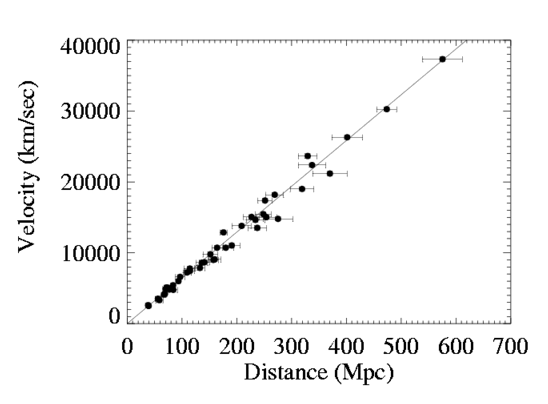 |
| Ris. 10.1
Habblovskaya diagramma (zavisimost' skorosti udaleniya
(v km/s),
izmerennoi po krasnomu smesheniyu, ot rasstoyaniya (v Mpk)) dlya
sverhnovyh tipa 1a. Tangens ugla naklona
pryamoi, approksimiruyushei etu zavisimost', daet sovremennoe znachenie
postoyannoi Habbla |
1933, F. Cvikki, skrytaya massa v skopleniyah galaktik
1949, Alfer, Bete, Gamov - gipoteza "goryachei Vselennoi"
("Big Bang") i predskazanie sushestvovaniya izotropnogo reliktovogo
izlucheniya s ravnovesnym spektrom s temperaturoi ![]() K
1965, A. Penzias, R. Vilson - otkrytie izotropnogo kosmicheskogo mikrovolnovogo
fona (reliktovoe izluchenie) s temperaturoi okolo 3 K.
K
1965, A. Penzias, R. Vilson - otkrytie izotropnogo kosmicheskogo mikrovolnovogo
fona (reliktovoe izluchenie) s temperaturoi okolo 3 K.
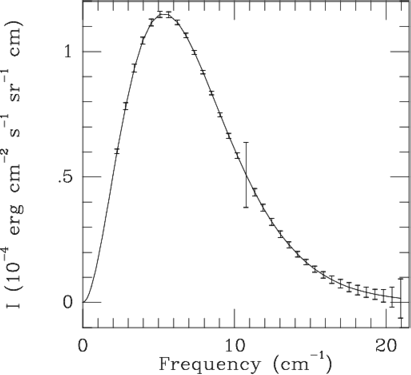 |
| Ris. 10.2 Spektr kosmicheskogo mikrovolnovogo (reliktovogo) izlucheniya. Sploshnaya krivaya - funkciya Planka dlya absolyutno chernogo tela s temperaturoi T=2.728 K. |
1979-80, A. Gus, A.A. Starobinskii, A.D. Linde, D.A. Kirzhnic - gipoteza
"inflyacionnoi" (razduvayusheisya) Vselennoi
1992-1993, v kosmicheskih eksperimentah "Relikt" (Rossiya),
"COBE" (SShA) obnaruzheny flyuktuacii reliktovogo
izlucheniya na urovne
![]() v masshtabah
okolo 10 gradusov.
1998, Habblovskie diagrammy (zavisimost' vidimaya
zvezdnaya velichina v maksimume bleska - krasnoe smeshenie)
dlya Sverhnovyh tipa Ia (termoyadernye
vzryvy belyh karlikov s massoi vblizi predela Chandrasekara)
pokazyvayut, chto na bol'shih rasstoyaniyah rasshirenie Vselnnoi proishodit
s uskoreniem. Eto ukazyvaet neizbezhnost' vvedeniya polozhitel'noi
kosmologicheskoi postoyannoi (Einshtein, 1917) ili bolee
slozhnogo vida materii (t.n. temnoi energii" ili "kvintessencii")
s uravneniem sostoyaniya
v masshtabah
okolo 10 gradusov.
1998, Habblovskie diagrammy (zavisimost' vidimaya
zvezdnaya velichina v maksimume bleska - krasnoe smeshenie)
dlya Sverhnovyh tipa Ia (termoyadernye
vzryvy belyh karlikov s massoi vblizi predela Chandrasekara)
pokazyvayut, chto na bol'shih rasstoyaniyah rasshirenie Vselnnoi proishodit
s uskoreniem. Eto ukazyvaet neizbezhnost' vvedeniya polozhitel'noi
kosmologicheskoi postoyannoi (Einshtein, 1917) ili bolee
slozhnogo vida materii (t.n. temnoi energii" ili "kvintessencii")
s uravneniem sostoyaniya
![]() , kotoraya daet maksimal'nyi vklad v sovremennuyu
plotnost'
energii Vselennoi (
, kotoraya daet maksimal'nyi vklad v sovremennuyu
plotnost'
energii Vselennoi (![]() ) i effektivno sozdaet antigravitaciyu na bol'shih
masshtabah.
2000, izmerenie uglovogo spektra flyuktuacii reliktovogo
mikrovolnovogo izlucheniya v eksperimentah
BOOMERanG i MAXIMA. Otkrytie pervogo dopplerovskogo pika v
uglovom spektre flyuktuacii na masshtabah okolo 1 gradusa,
predskazannogo A.D. Saharovym v 1967 g. (t.n. "Saharovskie
kolebaniya"). Dokazatel'stvo ploskoi (Evklidovoi) geometrii
prostranstvennyh sechenii nablyudaemoi Vselennoi
s tochnost'yu poryadka 10% do krasnyh smeshenii
) i effektivno sozdaet antigravitaciyu na bol'shih
masshtabah.
2000, izmerenie uglovogo spektra flyuktuacii reliktovogo
mikrovolnovogo izlucheniya v eksperimentah
BOOMERanG i MAXIMA. Otkrytie pervogo dopplerovskogo pika v
uglovom spektre flyuktuacii na masshtabah okolo 1 gradusa,
predskazannogo A.D. Saharovym v 1967 g. (t.n. "Saharovskie
kolebaniya"). Dokazatel'stvo ploskoi (Evklidovoi) geometrii
prostranstvennyh sechenii nablyudaemoi Vselennoi
s tochnost'yu poryadka 10% do krasnyh smeshenii ![]() (epoha rekombinacii) (Ris. 10.3 i 10.4).
(epoha rekombinacii) (Ris. 10.3 i 10.4).
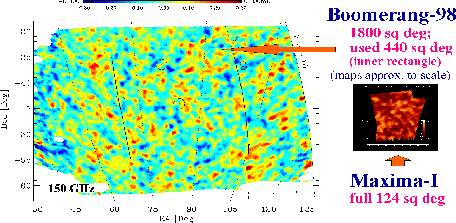 |
| Ris. 10.3 Karta flyuktuacii kosmicheskogo mikrovolnovogo izlucheniya v masshtabah ot 5 uglovyh minut do neskol'kih gradusov po dannym eksperimenta BOOMERanG (karta sleva) i MAHIMA (karta sprava). |
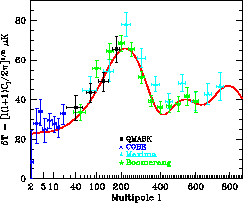 |
| Ris. 10.4
Uglovoi spektr flyuktuacii
reliktovogo izlucheniya po dannym eksperimentov BOOMERanG, MAXIMA i QMASK.
Polozhenie pervogo pika na |
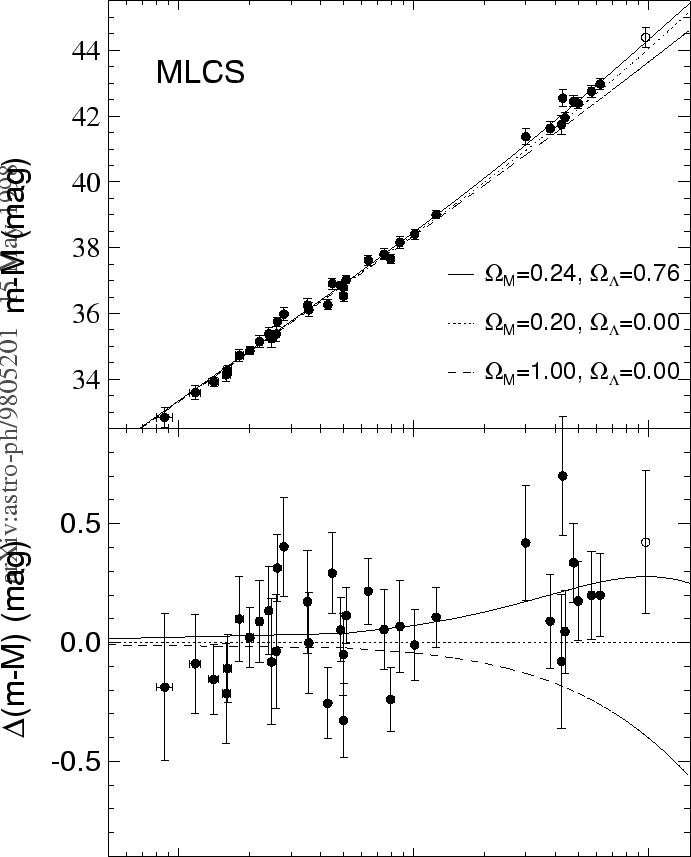 |
| Ris. 10.5 Habblovskaya diagramma vidimaya zvezdnaya velichina - krasnoe smeshenie dlya SN Ia, svidetel'stvuyushaya ob uskorennom rasshirenii Vselennoi v nastoyashee vremya (t.e. o preobladani polozhitel'noi kosmologicheskoi postoyannoi v sovremennoi dinamike Vselennoi). V nizhnei chasti risunka privedena raznica v module rasstoyaniya (vidimaya velichina - absolyutnaya velichina) dlya razlichnyh kosmologicheskih modelei. [Iz raboty A. Riess et al. 1998, AJ 116, 1009]. |
Nesmotrya na kolossal'nyi progress v sovremennoi kosmologii, mnogo vazhnyh voprosov octayutsya nereshennymi :
- Problema nebarionnoi skrytoi massy (nablyudaemoe veshestvo
vo Vselennoi sostavlyaet po masse ne bolee neskol'kih procentov
ot polnoi massy tyagoteyushego veshestva)
- Problema kosmologicheskoi postoyannoi (ili pochemu ne
vidna ogromnaya energiya nulevyh flyuktuacii vakuuma ?)
i primykayushaya k nei problema "kvintessencii" (substancii
neizvestnoi prirody, ne pokazyvayushei gravitacionnogo skuchivaniya i
imeyushei uravnenie sostoyaniya
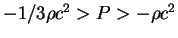 ),
sozdayushei v nastoyashee vremya antigravitaciyayu v bol'shih
masshtabah i delayushih Vselennuyu prakticheski ploskoi
),
sozdayushei v nastoyashee vremya antigravitaciyayu v bol'shih
masshtabah i delayushih Vselennuyu prakticheski ploskoi
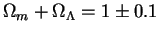 )
)
- Samaya rannyaya Vselennaya (kvantovoe rozhdenie, strela
vremeni, kosmologiya na 3-mernoi brane v mnogomernom prostranstve
i t.d.)
10.1.3 Zakon Habbla
.Snachala rassmotrim prosteishie odnorodnye i izotropnye kosmologicheskie modeli bez kosmologicheskoi postoyannoi. V silu odnorodnosti voz'mem v prostranstve ogranichennuyu sfericheskuyu oblast' i prosledim za ee evolyuciei. Vneshnie oblasti nesushestvenny, t.k. pole tyagoteniya, sozdavaemoe veshestvom vne sfery (pri strogoi sfericheskoi simmetrii) tozhdestvenno ravno nulyu (Tolmen 1934, dokazatel'stvo v ramkah OTO).
Zamechanie.
V n'yutonovskoi teorii tyagotenie opisyvaetsya uravneniem
![]() , i vnutri poloi sfery
, i vnutri poloi sfery
![]() , a n'yutonova teoriya lokal'no
yavlyaetsya tochnoi: dlya slabogo gravitacionnogo polya ili v lyuboi
dostatochno maloi okrestnosti skol' ugodno sil'nogo
gravitacionnogo polya mozhno
prostranstvo-vremya rassmatrivat' kak ploskoe, s metrikoi
, a n'yutonova teoriya lokal'no
yavlyaetsya tochnoi: dlya slabogo gravitacionnogo polya ili v lyuboi
dostatochno maloi okrestnosti skol' ugodno sil'nogo
gravitacionnogo polya mozhno
prostranstvo-vremya rassmatrivat' kak ploskoe, s metrikoi
![]() , gde
, gde
![]() -
metrika ploskogo prostranstva-vremeni Minkovskogo,
-
metrika ploskogo prostranstva-vremeni Minkovskogo, ![]() - malye
vozmusheniya metriki; dlya perehoda k n'yutonovskomu gravpotencialu
- malye
vozmusheniya metriki; dlya perehoda k n'yutonovskomu gravpotencialu
![]() mozhno pol'zovat'sya razlozheniem
mozhno pol'zovat'sya razlozheniem
![]() ,
,
![]() .
.
Kak sleduet iz astronomicheskih nablyudenii spektrov galaktik,
skorost' ih udaleniya ot nablyudatelya pryamo proporcional'na rasstoyaniyu:
Rassmotrim massu, zaklyuchennuyu vnutri vydelennogo shara radiusa ![]() :
:
![]() . Izmenenie plotnosti pri rasshirenii
. Izmenenie plotnosti pri rasshirenii
10.1.4 Zakon evolyucii. Kriticheskaya plotnost'
Rassmotrim tochku na granice oblasti,
rasshiryayusheisya po zakonu (10.1).
Uravnenie dvizheniya
Zametim, chto ni massa, ni radius shara v uravneniya ne voshli, sledovatel'no mozhem rasprostranit' rassmotrenie na bol'shie oblasti (odnako lish' do teh por, poka primenima N'yutonova gravitaciya).
Umnozhaya (10.3) na ![]() i integriruya,
poluchaem zakon sohraneniya energii
i integriruya,
poluchaem zakon sohraneniya energii
gde
est' tak nazyvaemya kriticheskaya plotnost' v moment
Zamechaniya.
1). Tak kak v nastoyashee vremya ![]() (krasnoe
smeshenie - Vselennaya rasshiryaetsya!), pervoe slagaemoe
(krasnoe
smeshenie - Vselennaya rasshiryaetsya!), pervoe slagaemoe ![]() vozrastaet s umen'sheniem
vozrastaet s umen'sheniem ![]() , a znachit v proshlom skorost' rasshireniya byla
bol'she (t.e. rasshirenie dolzhno zamedlyat'sya - ochevidnoe svoistvo
dvizheniya s uchetom tormozyashego deistviya gravitacii), i v rassmatrivaemoi
modeli v proshlom byl moment
takoi, chto
, a znachit v proshlom skorost' rasshireniya byla
bol'she (t.e. rasshirenie dolzhno zamedlyat'sya - ochevidnoe svoistvo
dvizheniya s uchetom tormozyashego deistviya gravitacii), i v rassmatrivaemoi
modeli v proshlom byl moment
takoi, chto
![]() i
i ![]() (singulyarnost').
Itak, proshloe celikom opredelyaetsya povedeniem pervogo slagaemogo
2) Budushee: celikom opredelyaetsya znakom vtorogo slagaemogo (konstanta
v zakone sohraneniya energii), t.e. sootnosheniem
(singulyarnost').
Itak, proshloe celikom opredelyaetsya povedeniem pervogo slagaemogo
2) Budushee: celikom opredelyaetsya znakom vtorogo slagaemogo (konstanta
v zakone sohraneniya energii), t.e. sootnosheniem
![]() :
A) Esli
:
A) Esli
![]() (
(![]() ) - vtoroe slagaemoe otricatel'noe,
rasshirenie tormozitsya i smenyaetsya szhatiem (t.k. pervoe slagaemoe
) - vtoroe slagaemoe otricatel'noe,
rasshirenie tormozitsya i smenyaetsya szhatiem (t.k. pervoe slagaemoe
![]() pri
pri ![]() ) - model' "zakrytoi Vselennoi",
polnaya energiya Vselennoi polozhitel'na;
V)
) - model' "zakrytoi Vselennoi",
polnaya energiya Vselennoi polozhitel'na;
V) ![]() , vtoroe slagaemoe polozhitel'no, i rasshirenie prodolzhaetsya
vechno s asimptoticheskoi skorost'yu
, vtoroe slagaemoe polozhitel'no, i rasshirenie prodolzhaetsya
vechno s asimptoticheskoi skorost'yu
![]() pri
pri ![]() - model' otkrytoi Vselennoi, polnaya energiya
Vselennoi otricatel'na;
C)
- model' otkrytoi Vselennoi, polnaya energiya
Vselennoi otricatel'na;
C) ![]() , rasshirenie prodolzhaetsya neogranichenno,
v predele s asimptoticheski
stremyasheisya k nulyu skorost'yu. Polnaya energiya ravna nulyu
(kineticheskaya energiya v lyuboi moment vremeni tochno kompensiruetsya
potencial'noi energiei)10.1.
3). Sovremennye nablyudeniya (Habblovskie diagrammy
dlya sverhnovyh tipa 1a) interpretiruyutsya kak ukazanie na
uskorennoe rasshirenie Vselennoi. Eto mozhno ob'yasnit', vvedya
v model' sily ottalkivaniya, deistvuyushie na bol'shih rasstoyaniyah.
Imenno takoi fizicheskii effekt okazyvaet
polozhitel'naya kosmologicheskaya postoyannaya, vvedennaya A.Einshteinom
v 1917 g. dlya polucheniya stacionarnyh reshenii OTO v primenenii ko
vsei Vselennoi.
, rasshirenie prodolzhaetsya neogranichenno,
v predele s asimptoticheski
stremyasheisya k nulyu skorost'yu. Polnaya energiya ravna nulyu
(kineticheskaya energiya v lyuboi moment vremeni tochno kompensiruetsya
potencial'noi energiei)10.1.
3). Sovremennye nablyudeniya (Habblovskie diagrammy
dlya sverhnovyh tipa 1a) interpretiruyutsya kak ukazanie na
uskorennoe rasshirenie Vselennoi. Eto mozhno ob'yasnit', vvedya
v model' sily ottalkivaniya, deistvuyushie na bol'shih rasstoyaniyah.
Imenno takoi fizicheskii effekt okazyvaet
polozhitel'naya kosmologicheskaya postoyannaya, vvedennaya A.Einshteinom
v 1917 g. dlya polucheniya stacionarnyh reshenii OTO v primenenii ko
vsei Vselennoi.
Podcherknem eshe raz, chto privedennye vyshe rassuzhdeniya otnosilis' k modelyam
Fridmana bez kosmologicheskoi postoyannoi. Vvedenie kosmologicheskoi
postoyannoi menyaet kartinu kachestvenno: nablyudaemoe segodnya
uskorenoe rasshirenie Vselennoi oznachaet uvelichenie postoyannoi Habbla
so vremenem. Odnako v proshlom obyazatel'no dolzhen byt'
moment, kogda masshtabnyi faktor ![]() uvelichivalsya s zamedleniem. Vazhno, chto do etogo momenta
(naprimer, v rannei Vselennoi)
kosmologicheskaya
postoyannaya ne igrala dinamicheskoi roli.
uvelichivalsya s zamedleniem. Vazhno, chto do etogo momenta
(naprimer, v rannei Vselennoi)
kosmologicheskaya
postoyannaya ne igrala dinamicheskoi roli.
10.1.4.1 Prodolzhitel'nost' rasshireniya i "Vozrast Vselennoi"
Prodolzhim rassmotrenie fridmanovskih modelei bez kosmologicheskoi
postoyannoi.
Zakon Habbla
![]() imeet prostuyu geometricheskuyu
interpretaciyu: tangens ugla naklona kasatel'noi k krivoi
imeet prostuyu geometricheskuyu
interpretaciyu: tangens ugla naklona kasatel'noi k krivoi ![]() v tochke
v tochke ![]() est'
est' ![]() , to est' vremya ot momenta peresecheniya
kasatel'noi osi vremeni
, to est' vremya ot momenta peresecheniya
kasatel'noi osi vremeni ![]() do momenta
do momenta ![]() :
:
![]() let. Na samom dele, real'nyi vozrast men'she (zavisit ot
konkretnogo vida funkcii
let. Na samom dele, real'nyi vozrast men'she (zavisit ot
konkretnogo vida funkcii ![]() )
)
10.1.4.2 Vazhnyi chastnyi sluchai
V etom sluchae konstanta v uravnenii energii tochno ravna nulyu,
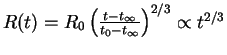 ,
,
dlya plotnosti: iz
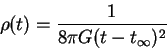
Zamechanie: v uravnenii (10.6) 2-i chlen
10.1.5 Vliyanie davleniya
Do sih por my rassmatrivali pyl' ili gaz nizkoi plotnosti
s davleniem ![]() (horoshee priblizhenie dlya sovremennoi
stadii rasshireniya). Dlya
obychnogo veshestva
(horoshee priblizhenie dlya sovremennoi
stadii rasshireniya). Dlya
obychnogo veshestva
![]() (
(
![]() - plotnost'
energii), dlya relyativistskih chastic (fotony, neitrino),
u kotoryh energiya proporcional'na impul'su
- plotnost'
energii), dlya relyativistskih chastic (fotony, neitrino),
u kotoryh energiya proporcional'na impul'su ![]() (tochnoe ravenstvo v sluchae bezmassovyh chastic)
(tochnoe ravenstvo v sluchae bezmassovyh chastic)
![]() . Dlya obychnogo veshestva plotnost' padaet kak kub
masshtabnogo faktora,
. Dlya obychnogo veshestva plotnost' padaet kak kub
masshtabnogo faktora,
![]() . Dlya relyativistskih
chastic (izlucheniya) pri adiabaticheskom rasshirenii plotnost' padaet
bystree, t.k. umen'shaetsya plotnost' fotonov v edinice ob'ema (
. Dlya relyativistskih
chastic (izlucheniya) pri adiabaticheskom rasshirenii plotnost' padaet
bystree, t.k. umen'shaetsya plotnost' fotonov v edinice ob'ema (![]() ) i umen'shaetsya energiya kazhdogo fotona (krasnoe smeshenie)
(
) i umen'shaetsya energiya kazhdogo fotona (krasnoe smeshenie)
(![]() ), poetomu
), poetomu
![]() .
Formal'nyi vyvod etogo sootnosheniya
sleduet iz 1 zakona termodinamiki: esli
est' davlenie, ono sovershaet rabotu nad sosednimi elementami
.
Formal'nyi vyvod etogo sootnosheniya
sleduet iz 1 zakona termodinamiki: esli
est' davlenie, ono sovershaet rabotu nad sosednimi elementami
![]() , dlya izlucheniya
, dlya izlucheniya ![]() , otkuda
, otkuda
![]() . Poskol'ku dlya izlucheniya v termodinamicheskom
ravnovesii (AChT)
. Poskol'ku dlya izlucheniya v termodinamicheskom
ravnovesii (AChT) ![]() , temperatura
v rasshiryayusheisya Vselennoi padaet obratno proporcional'no masshtabnomu
faktoru:
, temperatura
v rasshiryayusheisya Vselennoi padaet obratno proporcional'no masshtabnomu
faktoru: ![]() , chto, vprochem, ochevidno: s tochnost'yu do
konstant energiya = chastota = temperatura, a znachit
temperatura evolyucioniruet tak zhe, kak i chastota, t.e. proporcional'no
krasnomu smesheniyu.
, chto, vprochem, ochevidno: s tochnost'yu do
konstant energiya = chastota = temperatura, a znachit
temperatura evolyucioniruet tak zhe, kak i chastota, t.e. proporcional'no
krasnomu smesheniyu.
Eti prostye rassuzhdeniya pokazyvayut, chto
uhodya v proshloe, my dolzhny rano ili pozdno nachat'
uchityvat' vliyanie davleniya ![]() . Kak bylo pokazano Tolmenom,
v ramkah OTO uchet davleniya svoditsya k
zamene plotnosti na summu plotnosti energii i utroennogo davleniya:
. Kak bylo pokazano Tolmenom,
v ramkah OTO uchet davleniya svoditsya k
zamene plotnosti na summu plotnosti energii i utroennogo davleniya:
Togda uravnenie dvizheniya modificiruetsya v
Rassmotrim sluchai dominirovaniya izlucheniya, t.e. epohu, kogda plotnost'
energii celikom opredelyaetsya izlucheniem. Togda ![]() ,
,
![]() , gde
, gde ![]() nekotoraya postoyannaya.
Uravnenie energii pri etom stanovitsya
nekotoraya postoyannaya.
Uravnenie energii pri etom stanovitsya
Pri malyh
pri
<< 10. Kosmologiya | Oglavlenie | 10.2 Modeli Fridmana s >>
|
Publikacii s klyuchevymi slovami:
zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika
Publikacii so slovami: zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |