- ... radiusu1.1
Gravitacionnyi, ili Shvarcshil'dovskii
radius dlya massy
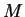 sootvetstvuet radiusu gorizonta sobytii pri sfericheski-
simmetrichnom kollapse tela pod deistviem gravitacii. S tochki
zreniya N'yutonovskoi
fiziki mozhno bylo by skazat', vsled za Laplasom, chto na etom
radiuse parabolicheskaya skorost' stanovitsya ravnoi skorosti sveta.
Telo s takim radiusom ne mozhet ispuskat' nikakie signaly.
sootvetstvuet radiusu gorizonta sobytii pri sfericheski-
simmetrichnom kollapse tela pod deistviem gravitacii. S tochki
zreniya N'yutonovskoi
fiziki mozhno bylo by skazat', vsled za Laplasom, chto na etom
radiuse parabolicheskaya skorost' stanovitsya ravnoi skorosti sveta.
Telo s takim radiusom ne mozhet ispuskat' nikakie signaly.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... rabotaet"1.2 Napomnim, chto sovremennaya fizika elementarnyh chastic proverena na uskoritelyah do energii poryadka TeV
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... izlucheniya"2.1 Nizhe my utochnim ponyatie temperatury izlucheniya
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... zapisat'2.2 Neprevzoidennyi po yasnosti i fizicheskoi glubine vyvod uravneniya perenosa i obsuzhdenie ego vazhneishih svoistv mozhno naiti v monografii Ya.B.Zel'dovicha i Yu.P.Raizera "Fizika udarnyh voln i vysokotemperaturnyh gidrodinamicheskih yavlenii", M., Nauka, 1966, gl. II.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ...shuma. 3.1 Gorazdo trudnee opredelit' polozhenie udalennogo istochnika v prostranstve - problema rasstoyanii odna iz osnovnyh v astronomii, dlya etogo nado znat' kak minimum svetimost' istochnika ili inye harakteristiki, vydelyayushie ego prostranstvennoe polozhenie. Naprimer, izmeryat' krasnoe smeshenie v spektrah udalennyh galaktik.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... geliem.3.2 Poyasnim smysl etoi formuly. Pust' istochnik izlucheniya predstavlyaet soboi nepreryvnyi shirokopolosnyi signal, nablyudaemyi v techenie vremeni
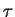 . Fonovyi signal budem harakterizovat' dispersiei
. Fonovyi signal budem harakterizovat' dispersiei 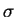 . Za
kriterii obnaruzhimosti signala na fone shuma voz'mem zadannoe otnoshenie
signala k shumu
. Za
kriterii obnaruzhimosti signala na fone shuma voz'mem zadannoe otnoshenie
signala k shumu 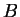 . Iz-za konechnosti (uzosti) polosy detektora shum mozhno
schitat' postoyannym, tak chto za vremya kogerentnosti
. Iz-za konechnosti (uzosti) polosy detektora shum mozhno
schitat' postoyannym, tak chto za vremya kogerentnosti
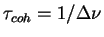 razlichnye realizacii shuma stanovyatsya neskorrelirovannymi, inymi slovami,
uchastki zapisi dlinoi
razlichnye realizacii shuma stanovyatsya neskorrelirovannymi, inymi slovami,
uchastki zapisi dlinoi 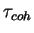 nezavisimy. Togda za vremya nakopleniya
signala
nezavisimy. Togda za vremya nakopleniya
signala 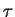 imeem
imeem
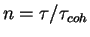 nezavisimyh realizacii fona, kazhdaya
iz kotoryh imeet dispersiyu
nezavisimyh realizacii fona, kazhdaya
iz kotoryh imeet dispersiyu 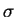 . Znachit, za vremya nablyudeniya dispersiya
fonovyh otschetov umen'shaetsya v
. Znachit, za vremya nablyudeniya dispersiya
fonovyh otschetov umen'shaetsya v 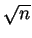 raz:
raz:
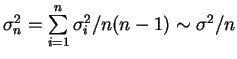 .
Minimal'no
obnaruzhimyi signal est'
.
Minimal'no
obnaruzhimyi signal est'
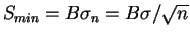 ,
otkuda i sleduet formula (3.4).
,
otkuda i sleduet formula (3.4).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... spekl-interferometrii3.3 ot angl. speckle - zernyshko
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... glaza3.4 S tochnost'yu do akkomodacii zrachka v polumrake kolodca
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ...
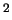 4.1
Zametim, chto sechenie
fotoionizacii atoma znachitel'no men'she, po poryadku ono ravno
kvadratu razmera Borovskoi orbity, s kotoroi vozbuzhdaetsya elektron.
Prichina zdes' ta zhe, chto i obsuzhdavsheesya v 1 lekcii prevoshodstvo
harakternoi dliny volny sveta, ispuskaemogo atomami pri svyazanno-svyazannyh
ili svobodno-svyazannyh perehodah, nad razmerom Borovskih orbit v
4.1
Zametim, chto sechenie
fotoionizacii atoma znachitel'no men'she, po poryadku ono ravno
kvadratu razmera Borovskoi orbity, s kotoroi vozbuzhdaetsya elektron.
Prichina zdes' ta zhe, chto i obsuzhdavsheesya v 1 lekcii prevoshodstvo
harakternoi dliny volny sveta, ispuskaemogo atomami pri svyazanno-svyazannyh
ili svobodno-svyazannyh perehodah, nad razmerom Borovskih orbit v
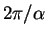 raz,
raz, 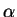 - postoyannaya tonkoi struktury
- postoyannaya tonkoi struktury
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... vremeni)4.2 Dlya kosmicheskoi plazmy eto oznachaet, chto odnovremenno vypolnyayutsya sleduyushie sootnosheniya:
- Maksvellovskoe raspredelenie chastic po skorostyam
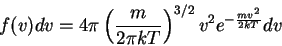
- Bol'cmanovskoe raspredelenie chastic po energiyam, kotoroe
dlya zaselennosti atomnyh urovnei s nomerami
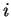 i
i 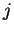 (cootvetstvenno, s energiyami
(cootvetstvenno, s energiyami 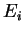 i
i 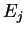 )
zapisyvaetsya v vide
)
zapisyvaetsya v vide
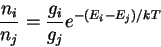
- zakon deistvuyushih mass dlya himicheskogo ravnovesiya, ili
v primenenii k usloviyam ionizovannoi plazmy - formula Saha
dlya stepeni ionizacii atomov i molekul
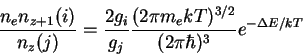
gde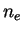 ,
, 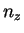 ,
, 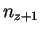 - koncentracii elektronov i ionov
- koncentracii elektronov i ionov
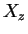 elementa H,
elementa H, 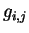 - statisticheskie vesa urovnei
- statisticheskie vesa urovnei 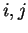 ionov,
ionov,
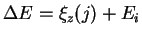 ,
, 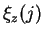 - energiya ionizacii s urovnya
- energiya ionizacii s urovnya 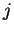 iona
iona
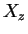 .
.
- Zakon izlucheniya Planka, zakon Kirhgofa i zakon Stefana-Bol'cmana
dlya AChT
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... sil4.3 V polnost'yu ionizovannoi plazme koncentraciya elektronov i ionov o odinakova
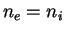 , a vremya ustanovleniya izotropnogo Maksvellovskogo
raspredeleniya dlya elektronnoi i ionnoi komponent ravny,
sootvetstvenno,
, a vremya ustanovleniya izotropnogo Maksvellovskogo
raspredeleniya dlya elektronnoi i ionnoi komponent ravny,
sootvetstvenno,
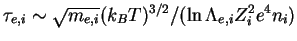 ,
gde
,
gde 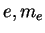 - zaryad elektrona i ego massa,
- zaryad elektrona i ego massa, 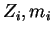 -
atomnyi nomer iona i ego massa,
-
atomnyi nomer iona i ego massa,
 -
Kulonovskii logarifm, uchityvayushii dal'nodeistvie kulonovskih sil.
Naprimer, dlya chisto vodorodnoi plazmy
(
-
Kulonovskii logarifm, uchityvayushii dal'nodeistvie kulonovskih sil.
Naprimer, dlya chisto vodorodnoi plazmy
(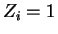 )
s
)
s 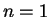 cm
cm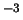 ,
, 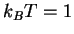 eV (
eV (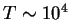 K) nahodim
K) nahodim
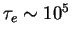 c
c
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... 4.4 Provodimost' - makroskopicheskaya harakteristika sredy, vhodyashaya v zakon Oma. Pri otsutstvii magnitnogo polya tok proporcionalen napryazhennosti polya
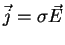 .
Dlya polnost'yu
ionizovannoi plazmy, v kotoroi preobladayut processy soudarenii chastic,
udel'naya provodimost' opredelyaetsya koncentraciei chastic
.
Dlya polnost'yu
ionizovannoi plazmy, v kotoroi preobladayut processy soudarenii chastic,
udel'naya provodimost' opredelyaetsya koncentraciei chastic 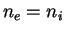 i
vremenem stolknovenii mezhdu elektronami i
ionami
i
vremenem stolknovenii mezhdu elektronami i
ionami  i ravna
i ravna
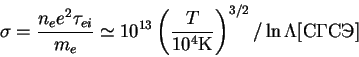
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... zreniya4.5 Etot rezul'tat dlya opticheski tonkoi sredy mozhno poluchit' ne reshaya uravneniya perenosa, vospol'zovavshis' fizicheskim smyslom ob'emnogo koefficienta izlucheniya i ego vyrazheniem cherez Einshteinovskii koefficient spontannogo izlucheniya (obratnoe vremya zhizni atoma v vozbuzhdennom sostoyanii)
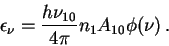
Dalee nado zapisat' zakon Kirhgofa dlya svyazi koefficientov izlucheniya i poglosheniya, otkuda neposredstvenno poluchitsya formula (4.8).. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... 3).4.6 Zdes' polnaya analogiya s uravneniem Van-der-Vaal'sa dlya neideal'nogo gaza - nemonotonnaya zavisimost'
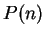 ob'yasnyaet razbienie sredy na dve fazy, zhidkuyu i gazoobraznuyu
ob'yasnyaet razbienie sredy na dve fazy, zhidkuyu i gazoobraznuyu
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... temperatury.4.7 Esli v plazme est' magnitnoe pole (a eto prakticheski vsegda tak), osnovnuyu rol' v vyravnivanii elektronnoi i ionnoi temperatury igrayut processy plazmennoi turbulentnosti, voznikayushei iz-za mnogochislennyh neustoichivostei, i kollektivnye processy v plazme (besstolknovitel'nye udarnye volny). Pri etom elektronnaya i ionnaya temperatury mogut sravnyat'sya za vremya mnogo koroche vremeni kulonovskih vzimodeistvii elektronov i ionov.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... rekombinacii4.8 Napomnim, chto dielektronnaya rekombinacii iona proishodit v dva etapa - snachala obrazuetsya neustoichivyi ion s dvumya vozbuzhdennymi elektronami i polozhitel'noi polnoi energiei (avtoionizaciya). Eto sostoyanie bystro raspadaetsya s izlucheniem fotona i polnaya energiya iona mozhet stat' otricatel'noi. Skorost' dielektronnoi rekombinacii nachinaet preobladat' nad radiacionnoi pri vysokih temperaturah
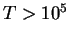 K.
K.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... elektrona)4.9 Tomsonovskoe priblizhenie dlya Komptonovskogo rasseyaniya primenimo do energii fotonov
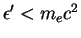 .
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... izlucheniya.4.10 Dlya raboty takoi teplovoi mashiny neobhodima kak minimum trehurovnevaya sistema po sheme
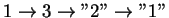 (nakachka na verhnii uroven' i stok na verhnii
(signal'nyi) uroven' mazernogo perehoda) ili
(nakachka na verhnii uroven' i stok na verhnii
(signal'nyi) uroven' mazernogo perehoda) ili
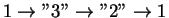 (nakachka na verhnii signal'nyi uroven' mazernogo perehoda "3" i stok
s nizhnego signal'nogo urovnya "2" na 1 uroven').
Otsutstvie ili oslablenie
stoka energii s verhnego urovnya "3" na verhnii signal'nyi "2" ili s nizhnego
signal'nogo "2"
urovnya privedet k umen'sheniyu zaselennosti
verhnego signal'nogo urovnya "2" v pervom sluchae, a otsutsvie stoka
s urovnya "2" vo vtorom sluchae privedet k povysheniyu naselennosti nizhnego
signal'nogo urovnya. V oboih sluchayah inversnaya zaselennost' signal'nyh
urovnei bystro ischeznet.
(nakachka na verhnii signal'nyi uroven' mazernogo perehoda "3" i stok
s nizhnego signal'nogo urovnya "2" na 1 uroven').
Otsutstvie ili oslablenie
stoka energii s verhnego urovnya "3" na verhnii signal'nyi "2" ili s nizhnego
signal'nogo "2"
urovnya privedet k umen'sheniyu zaselennosti
verhnego signal'nogo urovnya "2" v pervom sluchae, a otsutsvie stoka
s urovnya "2" vo vtorom sluchae privedet k povysheniyu naselennosti nizhnego
signal'nogo urovnya. V oboih sluchayah inversnaya zaselennost' signal'nyh
urovnei bystro ischeznet.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... sechenie4.11 Dlya relyativistskih protonov teh zhe energii sinhrotronnye poteri v
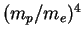 raz men'she
raz men'she
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ...
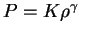 5.1
Chasto vmesto pokazatelya adiabaty
ispol'zuyut t.n. indeks politropy
5.1
Chasto vmesto pokazatelya adiabaty
ispol'zuyut t.n. indeks politropy 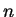 , svyazannyi s pokazatelem adiabaty
sootnosheniem
, svyazannyi s pokazatelem adiabaty
sootnosheniem
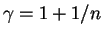 .
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ...
 6.1
Napomnim, chto
temperatura v 1 eV primerno sootvetstvuet 11000 K
6.1
Napomnim, chto
temperatura v 1 eV primerno sootvetstvuet 11000 K
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... rasseivayutsya6.2 Srednyaya dlina svobodnogo probega v centre Solnca po tomsonovskomu rasseyaniyu
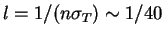 sm
sm
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... evolyucii7.1 Eto svyazano v pervuyu ochered' s uvelicheniem radiusa zvezdy i izmeneniem neprozrachnosti
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... imeetsya7.2 Etot uroven' yadra C
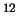 byl predskazan F.Hoilom dlya ob'yasneniya
sinteza elementov v zvezdam i pozdnee obnaruzhen V. Faulerom
byl predskazan F.Hoilom dlya ob'yasneniya
sinteza elementov v zvezdam i pozdnee obnaruzhen V. Faulerom
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... temperaturu8.1 Yarkostnaya temperatura ne prevyshaet fizicheskuyu temperaturu tela, ravnyayas' ei v sluchae absolyutno chernogo tela.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... granice9.1 Predpolagaetsya, chto vneshnii radius diska mnogo bol'she vnutrennego,
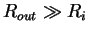 .
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... orbitoi9.2 Eto chisto relyativistskii effekt - v klassicheskoi zadache Keplera, kak izvestno, est' centrobezhnyi bar'er i orbity ustoichivy vplot' do
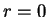 .
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ....11.1 Napomnim, chto v rasshiryayusheisya Vselennoi interval zapisyvaetsya v vide
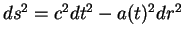 , gde
, gde 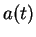 - masshtabnyi faktor, vid
kotorogo zavisit ot
uravneniya sostoyaniya, poetomu fizicheskoe rasstoyanie (t.e. izmeryaemoe s
pomosh'yu zhestkoi lineiki ili putem obmena svetovymi signalami) mezhdu dvumya
tochkami s postoyannymi koordinatami izmenyaetsya so vremenem kak
- masshtabnyi faktor, vid
kotorogo zavisit ot
uravneniya sostoyaniya, poetomu fizicheskoe rasstoyanie (t.e. izmeryaemoe s
pomosh'yu zhestkoi lineiki ili putem obmena svetovymi signalami) mezhdu dvumya
tochkami s postoyannymi koordinatami izmenyaetsya so vremenem kak
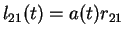 .
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... faktora12.1 Dlya prostoty rassmatrivaem sluchai bez kosmologicheskoi postoyannoi; v sluchae
 ee rol' dinamicheski ne vazhna
pri malyh masshtabnyh faktorah
ee rol' dinamicheski ne vazhna
pri malyh masshtabnyh faktorah
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ...
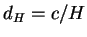 12.2
Na fridmanovskoi
stadii Habblovskaya dlina poryadka gorizonta
12.2
Na fridmanovskoi
stadii Habblovskaya dlina poryadka gorizonta
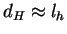 .
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ...
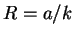 12.3
Dlya ploskoi modeli
12.3
Dlya ploskoi modeli 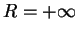
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... stranen.12.4 Naglyadnaya analogiya - neustoichivoe mahanicheskoe ravnovesie karandasha na stole. Esli karandash ustanovlen tochno po vertikali, pri otsutstvii vneshnih vozdeistvii on ostanetsya v etom polozhenii beskonechno dolgo (
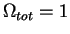 ). Maleishee otklonenie ot vertikali vedet k
bystroi poteri ustoichivosti (
). Maleishee otklonenie ot vertikali vedet k
bystroi poteri ustoichivosti (
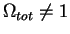 ).
).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... celom14.1 V sluchae
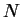 nekogerentnyh izluchatelei intensivnost'
vyhodyashego izlucheniya proporcional'na chislu chastic,
nekogerentnyh izluchatelei intensivnost'
vyhodyashego izlucheniya proporcional'na chislu chastic,
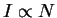 ,
t.k. v unosimuyu energiyu
dayut vklad kvadraty amplitud otdel'nyh izluchatelei. V sluchae kogerentnogo
(sinfaznogo) izlucheniya, skladyvayutsya sami amplitudy, poetomu
,
t.k. v unosimuyu energiyu
dayut vklad kvadraty amplitud otdel'nyh izluchatelei. V sluchae kogerentnogo
(sinfaznogo) izlucheniya, skladyvayutsya sami amplitudy, poetomu
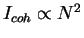
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... materiya14.2 V ramkah nashego obshego kursa my ne budem rassmatrivat' al'ternativnye teorii. Astrofizicheskie dannye s tochnost'yu luchshe 1% ubeditel'no podtverzhdayut vse vyvody OTO, i poka net nikakih astronomicheskih ukazanii na nevernost' koncepcii OTO.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... polya14.3 T.e. takogo polya, v kotorom skorosti svobodnogo dvizheniya mnogo men'she skorosti sveta
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ...
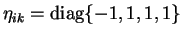 14.4
Dlya nevrashayushegosya sfericheski-simmetrichnogo
tela s massoi
14.4
Dlya nevrashayushegosya sfericheski-simmetrichnogo
tela s massoi 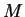 i radiusom
i radiusom 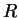 eti otlichiya poryadka
eti otlichiya poryadka 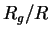 , gde
, gde
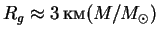 - gravitacionnyi radius.
- gravitacionnyi radius.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... ryabi.14.5 Konechno, nado ponimat' vsyu uslovnost' etoi analogii - naprimer, vzaimnoe izmenenie rasstoyanii mezhdu probnymi telami v pole gravitacionnoi volny ne zavisit ot massy samih tel, a bol'shoi korabl' v okeane melkuyu ryab' voobshe ne chuvstvuet!
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... Keplera14.6 Predpolagaetsya N'yutonovskoe priblizhenie i zamknutye orbity.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
- ... rabotaet"1.2 Napomnim, chto sovremennaya fizika elementarnyh chastic proverena na uskoritelyah do energii poryadka TeV
|
Publikacii s klyuchevymi slovami:
zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika
Publikacii so slovami: zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
Mneniya chitatelei [70]
Astrometriya
-
Astronomicheskie instrumenty
-
Astronomicheskoe obrazovanie
-
Astrofizika
-
Istoriya astronomii
-
Kosmonavtika, issledovanie kosmosa
-
Lyubitel'skaya astronomiya
-
Planety i Solnechnaya sistema
-
Solnce