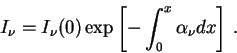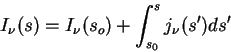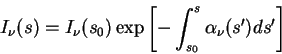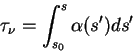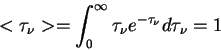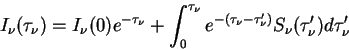<< 2.1 Uravnenie perenosa | Oglavlenie | 2.3 Teplovoe izluchenie >>
- 2.2.1 Koefficient izlucheniya
- 2.2.2 Koefficient poglosheniya
- 2.2.3 Uravnenie perenosa izlucheniya izlucheniya
- 2.2.4 Opticheskaya tolsha. Svyaz' s dlinoi svobodnogo probega
- 2.2.5 Funkciya istochnika
- 2.2.6 Formal'noe reshenie uravneniya perenosa
2.2 Uravnenie perenosa izlucheniya
Pereidem k opisaniyu rasprostraneniya izlucheniya v srede, s kotoroi vzaimodeistvuet izlucheniya. Vzaimodeistvie izlucheniya i veshestva mozhno rassmatrivat' na razlichnyh fizicheskih urovnyah. Dlya nashih celei budet dostatochno vvedeniya makroskopichesskih koefficientov izlucheniya i poglosheniya sveta, hotya raschet samih koefficientov kak fcnkciyu chastoty fotona i fizicheskih harakteristik sredy provoditsya klassicheskimi elektrodinaicheskimi i kvantovymi metodami.
2.2.1 Koefficient izlucheniya
Koefficientom izlucheniya nazyvaetsya
energiiya, izluchaemaya edinicei ob'ema za edinicu vremeni
v intervale chastot ![]() v napravlenii
v napravlenii ![]() :
:
V izluchayushei srede bez poglosheniya
za vremya ![]() fotony prohodyat put'
fotony prohodyat put' ![]() i dobavka k intensivnosti iz elementarnogo
ob'ema
i dobavka k intensivnosti iz elementarnogo
ob'ema ![]() budet
budet
![]() . Takim obrazom,
uravnenie perenosa priobretaet vid
. Takim obrazom,
uravnenie perenosa priobretaet vid
2.2.2 Koefficient poglosheniya
Pri prohozhdenii puti ![]() v pogloshayushei srede chast' fotonov
vybyvaet iz puchka (pogloshaetsya), i takim obrazom
fenomenologicheski mozhno zapisat'
v pogloshayushei srede chast' fotonov
vybyvaet iz puchka (pogloshaetsya), i takim obrazom
fenomenologicheski mozhno zapisat'
![]() ,
gde
,
gde
![]() - koefficient poglosheniya,
zavisyashii ot fizicheskih parametrov sredy. Intensivnost' puchka
umen'shaetsya posle prohozhdeniya rasstoyaniya
- koefficient poglosheniya,
zavisyashii ot fizicheskih parametrov sredy. Intensivnost' puchka
umen'shaetsya posle prohozhdeniya rasstoyaniya ![]() ot tochki
ot tochki ![]() do
tochki
do
tochki ![]() po eksponencial'nomu zakonu
po eksponencial'nomu zakonu
Inogda vvodyat koefficient poglosheniya na gramm
proidennogo veshestva,
![]() . V etom sluchae
koefficient
. V etom sluchae
koefficient ![]() sm
sm![]() /g nazyvaetsya
koefficientom neprozrachnosti.
Fizicheskii smysl koefficienta neprozrachnosti prost.
Otnesennyi k odnomu atomu, etot koefficient zavisit tol'ko ot
svoistv samogo atoma. Eta velichina
/g nazyvaetsya
koefficientom neprozrachnosti.
Fizicheskii smysl koefficienta neprozrachnosti prost.
Otnesennyi k odnomu atomu, etot koefficient zavisit tol'ko ot
svoistv samogo atoma. Eta velichina
![]() (
(![]() - plotnost' chisla chastic)
imeet razmernost' sm
- plotnost' chisla chastic)
imeet razmernost' sm![]() i nosit nazvanie effektivnogo secheniya
poglosheniya. Pust' parallel'nyi puchok sveta s chastotoi
i nosit nazvanie effektivnogo secheniya
poglosheniya. Pust' parallel'nyi puchok sveta s chastotoi ![]() s
secheniem 1 sm
s
secheniem 1 sm![]() prohodit cherez pogloshayushii gaz. Pogloshenie mozhno
predstavit' sebe tak, budto kazhdyi atom zamenen nekim malym neprozrachnym
diskom, perpendikulyarnym k napravleniyu puchka, popadaya v kotoryi kvant
zastrevaet (pogloshaetsya). Esli ploshad' kazhdogo diska
prohodit cherez pogloshayushii gaz. Pogloshenie mozhno
predstavit' sebe tak, budto kazhdyi atom zamenen nekim malym neprozrachnym
diskom, perpendikulyarnym k napravleniyu puchka, popadaya v kotoryi kvant
zastrevaet (pogloshaetsya). Esli ploshad' kazhdogo diska ![]() ,
a koncentraciya
,
a koncentraciya ![]() v kub. sm, to polnaya ploshad' vseh diskov
v sloe gaza s ploshad'yu 1 sm
v kub. sm, to polnaya ploshad' vseh diskov
v sloe gaza s ploshad'yu 1 sm![]() i tolshinoi
i tolshinoi ![]() ravna
ravna
![]() .
otsyuda neposredstvenno poluchaem
.
otsyuda neposredstvenno poluchaem
![]() .
.
ZAMEChANIE: koefficient poglosheniya mozhet byt' kak polozhitel'nym (istinnoe pogloshenie), tak i otricatel'nym, t.k. v elementarnyh processah ispuskaniya i poglosheniya sveta atomami vsegda est' vynuzhdennoe (inducirovannoe) izluchenie, proporcional'noe, kak i pogloshenie, padayushei intensivnosti. Horosho izvestnyi primer iz optiki - kvantovyi generator izlucheniya (lazer). V kosmicheskih usloviyah takzhe vozmozhno obrazovanie inversnoi zaselennosti urovnei (komicheskie mazery). My obsudim etot vopros podrobne v lekcii, posvyashennoi mezhzvezdnoi srede.
2.2.3 Uravnenie perenosa
Esli sreda sposobna kak izluchat', tak i
pogloshat' svet, to, polagaya koefficienty
izlucheniya ![]() i poglosheniya
i poglosheniya ![]() izvestnymi funkciyami koordinat i vremeni,
zavisyashimi ot fizicheskogo sostoyaniya veshestva (temperatury,
plotnosti, himicheskogo sostava i t.d.), v stacionarnom sluchae
mozhem zapisat'
2.2
izvestnymi funkciyami koordinat i vremeni,
zavisyashimi ot fizicheskogo sostoyaniya veshestva (temperatury,
plotnosti, himicheskogo sostava i t.d.), v stacionarnom sluchae
mozhem zapisat'
2.2
Zamechanie 1. Fotony iz puchka mogut ischezat' ne tol'ko iz-za istinnogo poglosheniya, no i iz-za rasseyaniya (vo mnogih real'nyh usloviyah, naprimer, v solnechnoi korone, preobladaet rasseyanie na svobodnyh elektronah). Togda situaciya znachitel'no uslozhnyaetsya, poskol'ku rasseyanie izmenyaet traektorii fotonov, i uravnenie perenosa prevrashaetsya v integro-differencial'noe uravnenie, kotoroe reshaetsya, kak pravilo, chislennymi metodami.
Zamechanie 2. Prosteishie chastnye sluchai uravneniya perenosa (2.15):
1. Pust' sreda tol'ko izluchaet, ![]() ,
,
![]() ,
,
2. Pust' sreda tol'ko pogloshaet, ![]() ,
,
![]()
2.2.4 Opticheskaya tolsha. Svyaz' s dlinoi svobodnogo probega
Vvedem bezrazmernuyu harakteristiku vdol' lucha rasprostraneniya
sveta - opticheskuyu tolshinu sredy:
(inogda otschet rasstoyaniya vedetsya v obratnom napravlenii ot nablyudatelya k istochniku, togda v opredelenii opticheskoi tolshi poyavlyaetsya znak minus).
Esli ![]() , to realizuetsya
opticheski tolstyi sluchai (sreda neprozrachna
dlya izlucheniya);
esli
, to realizuetsya
opticheski tolstyi sluchai (sreda neprozrachna
dlya izlucheniya);
esli ![]() - opticheski tonkii sluchai (sreda prozrachna dlya
izlucheniya).
- opticheski tonkii sluchai (sreda prozrachna dlya
izlucheniya).
Vazhnost' ponyatiya opticheskoi tolshi vytekaet iz ee svyazi
s dlinoi svobodnogo probega fotona. Rassmotrim
odnorodnuyu sredu bez izlucheniya. Uravnenie perenosa mozhno perepisat'
v vide
![]() , t.e. veroyatnost' fotonu proiti dlinu,
sootvetstvuyushuyu
, t.e. veroyatnost' fotonu proiti dlinu,
sootvetstvuyushuyu ![]() ,
est'
,
est' ![]() , pri etom srednyaya opticheskaya tolsha
, pri etom srednyaya opticheskaya tolsha
Srednyaya dlina svobodnogo probega fotona
opredelyaetsya iz usloviya
![]() ,
,
2.2.5 Funkciya istochnika
Uravnenie perenosa (2.15) zapishem v vide:
gde
![]() - funkciya istochnika.
Celesoobraznost' vvedeniya etoi funkcii svyazana s tem, chto
chasto ona nahoditsya ili vychislyaetsya proshe, chem mikroskopicheskie
koefficienty izlucheniya ili poglosheniya.
Kak uvidim nizhe, dlya teplovogo izlucheniya
funkciya istochnika predstavlyaet soboi funkciyu Planka dlya
ravnovesnogo izlucheniya.
- funkciya istochnika.
Celesoobraznost' vvedeniya etoi funkcii svyazana s tem, chto
chasto ona nahoditsya ili vychislyaetsya proshe, chem mikroskopicheskie
koefficienty izlucheniya ili poglosheniya.
Kak uvidim nizhe, dlya teplovogo izlucheniya
funkciya istochnika predstavlyaet soboi funkciyu Planka dlya
ravnovesnogo izlucheniya.
2.2.6 Formal'noe reshenie uravneniya perenosa
Umnozhiv uravnenie (2.22)
na integriruyushii mnozhitel' ![]() , poluchaem reshenie
, poluchaem reshenie
Fizicheskii smysl etogo resheniya prost. 1-e slagaemoe:
nachal'noe izluchenie umen'shilos' v ![]() raz
iz-za poglosheniya; 2-e slagaemoe: istochnik, prointegrirovannyi
vdol' lucha zreniya s uchetom poglosheniya.
raz
iz-za poglosheniya; 2-e slagaemoe: istochnik, prointegrirovannyi
vdol' lucha zreniya s uchetom poglosheniya.
Eto reshenie pokazyvaet vazhnost' opredelniya funkcii istochnika kak funkcii opticheskoi glubiny. Esli ona izvestna, reshenie vypisano vyshe (2.23). Odnako vo mnogih real'nyh situaciyah funkciya istochnika zaranee neizvestna, poetomu reshenie uravneniya perenosa yavlyaetsya slozhnoi zadachei.
Rassmotrim neskol'ko vazhnyh primerov.
Primer 1. Pust' funkciya istochnika postoyanna v srede, t.e.
ne zavisit ot opticheskoi glubiny,
![]() . Togda
. Togda
Eto reshenie imeet prostoi fizicheskii smysl:
1) v predele bol'shih opticheskih
tolshin
![]() intensivnost' izlucheniya
stanovitsya ravnoi funkcii istochnika
intensivnost' izlucheniya
stanovitsya ravnoi funkcii istochnika
![]() .
(Ostorozhnee! Esli v srede est' rasseyanie, to intensivnost'
sama daet vklad v funkciyu istochnika, i
kartina sil'no uslozhnyaetsya).
2) Esli
.
(Ostorozhnee! Esli v srede est' rasseyanie, to intensivnost'
sama daet vklad v funkciyu istochnika, i
kartina sil'no uslozhnyaetsya).
2) Esli ![]() , to
, to ![]() ,
, ![]() umen'shaetsya vdol' lucha
3) Esli
umen'shaetsya vdol' lucha
3) Esli ![]() , to
, to ![]() ,
, ![]() vozrastaet vdol' lucha
Zaklyuchenie: Intensivnost' VSEGDA stremitsya k funkcii istochnika
vozrastaet vdol' lucha
Zaklyuchenie: Intensivnost' VSEGDA stremitsya k funkcii istochnika
Primer 2: Obrazovanie spektral'nyh linii.
Spektral'nye linii (izlucheniya ili poglosheniya)
obrazuyutsya togda, kogda est' vydelennye chastoty, na kotoryh
mikroskopicheskie koefficienty izlucheniya
![]() i poglosheniya
i poglosheniya ![]() kak funkcii chastoty imeyut ekstremumy.
Pust', naprimer, koefficient
poglosheniya imeet ostryi maksimum na chastote
kak funkcii chastoty imeyut ekstremumy.
Pust', naprimer, koefficient
poglosheniya imeet ostryi maksimum na chastote ![]() .
Pust' dlya prostoty funkciya istochnika ne menyaetsya s glubinoi.
Vozmozhny neskol'ko
variantov nablyudaemogo izlucheniya.
.
Pust' dlya prostoty funkciya istochnika ne menyaetsya s glubinoi.
Vozmozhny neskol'ko
variantov nablyudaemogo izlucheniya.
2a). Sreda opticheski tolstaya na vseh chastotah ![]() .
Linii net, viden nepreryvnyi spektr.
.
Linii net, viden nepreryvnyi spektr.
2b). Sreda opticheski tonkaya, ![]() na vseh chastotah, fonovoi
podsvetki net (
na vseh chastotah, fonovoi
podsvetki net (![]() ). V sootvetstvii s (2.24), nablyudaetsya
liniya izlucheniya na chastote
). V sootvetstvii s (2.24), nablyudaetsya
liniya izlucheniya na chastote ![]() , prichem ee maksimal'naya
intensivnost' men'she funkcii istochnika
, prichem ee maksimal'naya
intensivnost' men'she funkcii istochnika
![]() .
.
2v). Nichego kachestvenno ne izmenyaetsya v sluchae, esli
est' fonovaya podsvetka
![]() .
.
2g). Kachestvenno inaya kartina, esli fonovaya podsvetka bol'she funkcii
istochnika
![]() - poyavlyaetsya liniya poglosheniya.
- poyavlyaetsya liniya poglosheniya.
2d)-2e). Dlya sluchaya bol'shoi opticheskoi tolshi v centre linii,
![]() , kartina kachestvenno ne menyaetsya, za isklyucheniem
dostizheniya v linii velichiny funkcii istochnika.
, kartina kachestvenno ne menyaetsya, za isklyucheniem
dostizheniya v linii velichiny funkcii istochnika.
Eti sluchai proillyustrirovany na Ris. (2.3).
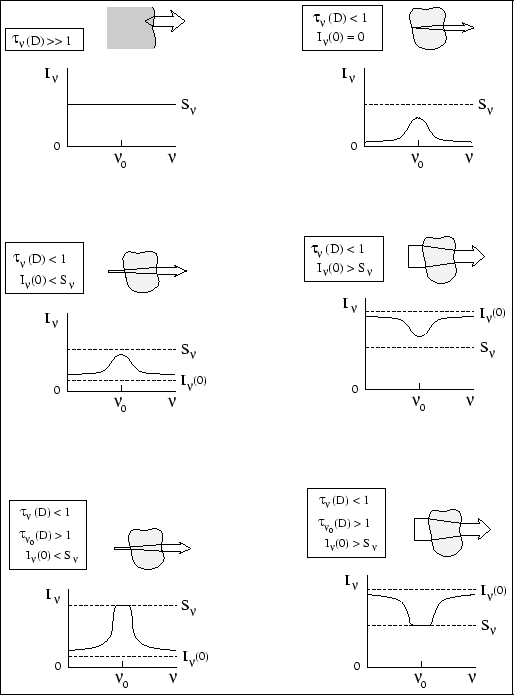 |
| Ris. 2.1
Obrazovanie spektral'nyh linii v odnorodnyh oblakah.
Linii ne obrazuyutsya, kogda oblako opticheski tolstoe (sleva vverhu).
V opticheski tonkom oblake linii obrazuyutsya tol'ko
esli ono "podsvecheno"
( |
<< 2.1 Uravnenie perenosa | Oglavlenie | 2.3 Teplovoe izluchenie >>
|
Publikacii s klyuchevymi slovami:
zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika
Publikacii so slovami: zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |