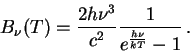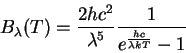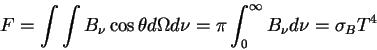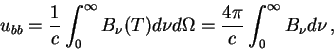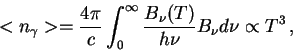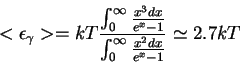<< 2.2 Uravnenie perenosa | Oglavlenie | 2.4 Harakteristicheskie temp... >>
2.3 Teplovoe izluchenie
Teplovoe izluchenie porozhdaetsya veshestvom, nahodyashimsya v teplovom ravnovesii.
2.3.1 Absolyutno chernoe telo
Vazhneishii primer teplovogo izlucheniya predstavlyaet soboi
izlucheniya absolyutno chernogo tela (AChT).
Izluchenie AChT nahoditsya v polnom termodinamicheskom ravnovesii.
Napomnim kratko snovnye svoistva izlucheniya AChT.
1). Spektr AChT (Plankovskii spektr:
![]() - funkciya Planka)
zavisit tol'ko ot temperatury
- funkciya Planka)
zavisit tol'ko ot temperatury ![]() , pole ravnovesnogo izlucheniya
strogo izotropno (t.e. polnyi potok cherez proizvol'no
orientirovannuyu ploshadku strogo raven nulyu),
nepolyarizovano.
2). Zakon Kirhgofa (spravedliv dlya lyubogo teplovogo izlucheniya)
, pole ravnovesnogo izlucheniya
strogo izotropno (t.e. polnyi potok cherez proizvol'no
orientirovannuyu ploshadku strogo raven nulyu),
nepolyarizovano.
2). Zakon Kirhgofa (spravedliv dlya lyubogo teplovogo izlucheniya)
Izluchenie, dlya kotorogo funkciya istochnika otlichaetsya ot funkcii Planka, nazyvaetsya neteplovym (primery neteplovogo izlucheniya - sinhrotronnoe izluchenie relyativistskih elektronov v magnitnom pole, obratnoe komptonovaskoe rasseyanie, cherenkovskoe izluchenie i t.d.)
Vazhnyi vyvod, sleduyushii iz uravneniya perenosa: lyuboe teplovoe izluchenie prevrashaetsya v izluchenie AChT v predele bol'shih opticheskih tolshin.
2.3.2 Zakon Planka dlya AChT
Funkciya Planka dlya ravnovesnogo izlucheniya
mozhet byt' zapisana v vide udel'noi intensivnosti
v edinichnom intervale chastot ([erg/sm![]() /c/Gc/ster])
/c/Gc/ster])
Chtoby pereiti k udel'noi intensivnosti v
edinichnom intervalu dlin voln, vospol'zuemsya zakonom sohraneniya
energii
![]() i svyaz'yu
i svyaz'yu ![]() . Nahodim
. Nahodim
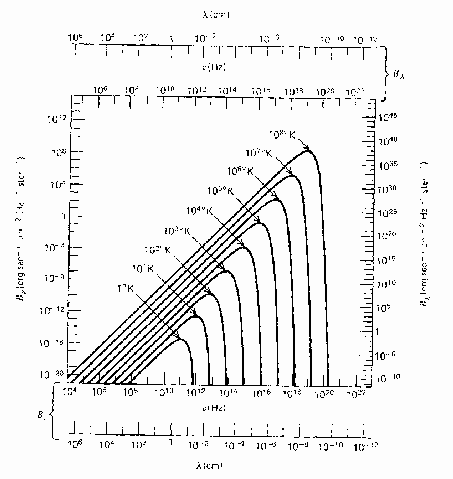
Funkciya Planka privedena na Ris. (2.4)
2.3.2.1 Predel'nye sluchai i svoistva funkcii Planka
- Zakon Releya-Dzhinsa,
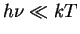 ,
,
Obratim vnimanie, chto v vyrazhenie dlya intensivnosti v etom sluchae ne voshla postoyannaya Planka, t.e. v etom predele formula opisyvaet chisto klassicheskoe izluchenie. Popytka ekstrapolirovat' zakon Releya-Dzhinsa v oblast' bolee vysokih chastot privodit k rashodimosti,
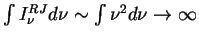 ("ul'trafioletovaya katastrofa")
("ul'trafioletovaya katastrofa")
- Zakon Vina,
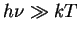
- Monotonnoe izmenenie s temperaturoi:
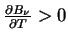 na vseh
na vseh 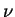 . Eto oznachaet, chto krivye funkcii
Planka dlya raznyh temperatur nigde ne peresekayutsya drug s drugom,
poankovskaya krivaya s temperaturoi
. Eto oznachaet, chto krivye funkcii
Planka dlya raznyh temperatur nigde ne peresekayutsya drug s drugom,
poankovskaya krivaya s temperaturoi 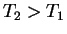 celikom lezhit vyshe krivoi
s temperaturoi
celikom lezhit vyshe krivoi
s temperaturoi 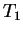 .
.
- Zakon smesheniya Vina
Opredelim maksimum v spektre AChT. Nachnem s udel'noi intensivnosti na edinichnyi interval chastot
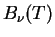 .
.
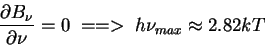
Maksimum funkcii
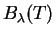 :
:
Podcherknem, chto
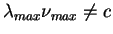 !!!
!!!
- Zakon Stefana-Bol'cmana
Polnyi potok energii s ploshadki, izluchayushei kak AChT, proporcionalen chetvertoi stepeni temperatury.
gde
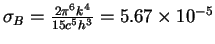 erg/sm
erg/sm /c/grad -
postoyannaya Stefana-Bol'cmana.
/c/grad -
postoyannaya Stefana-Bol'cmana.
- Plotnost' energii i davlenie ravnovesnogo izlucheniya
Plotnost' energii AChT
ili pol'zuyas' rezul'tatom (2.31)
gde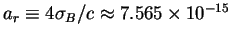 [erg/sm
[erg/sm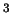 /grad
/grad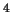 ] - postoyannaya plotnosti izlucheniya. Davlenie
ravnovesnogo izlucheniya
(2.10) pri etom ravno
] - postoyannaya plotnosti izlucheniya. Davlenie
ravnovesnogo izlucheniya
(2.10) pri etom ravno
- Srednyaya energiya chernotel'nogo fotona
Po opredeleniyu, eto velichina
Delaya zamenu peremennyh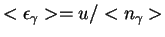 , gde
, gde
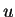 - plotnost' energii,
- plotnost' energii, 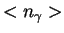 - plotnost' chisla kvantov.
Dlya AChT plotnost' energii est' (2.32),
- plotnost' chisla kvantov.
Dlya AChT plotnost' energii est' (2.32),
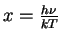 v integralah prihodim k
v integralah prihodim k
Fermievskie integraly v chislitele i znamenatele svodyatsya k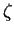 -funkcii
Rimana
-funkcii
Rimana
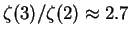 ,
v priblizhenii Vina eto prosto gamma-funkcii
,
v priblizhenii Vina eto prosto gamma-funkcii
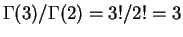 .
.
Ochen' poleznoe priblizhenie dlya plotnosti chisla fotonov chernotel'nogo
izlucheniya poluchaetsya s ispol'zovaniem priblizheniya Vina:
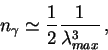
gde
<< 2.2 Uravnenie perenosa | Oglavlenie | 2.4 Harakteristicheskie temp... >>
|
Publikacii s klyuchevymi slovami:
zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika
Publikacii so slovami: zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |