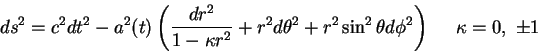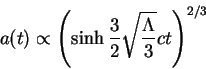<< 10.1 Klassicheskaya kosmologiya | Oglavlenie | 11. Kosmologiya (prodolzhenie) >>
10.2 Modeli Fridmana s komologicheskoi postoyannoi
Kak otmechalos' vyshe, sovremennye dannye ubeditel'no svidetel'stvuyut v pol'zu nalichiya znachitel'noi doli polnoi energii Vselennoi v forme kosmologicheskoi postoyannoi. Poetomu nizhe dlya spravok my privodim osnovnye formuly modeli odnorodnoi izotropnoi Vslennoi (model' Fridmana- Robertsona-Uokera) s kosmologicheskoi postoyannoi.
Odnorodnaya i izotropnaya Vselennaya mozhet byt' opisana nestacionarnoi
(t.e. zavisyashei ot vremeni) metrikoi special'nogo vida
(t.n. metrika Fridmana-Robertsona-Uokera)
opredelyaet odnu iz treh vozmozhnyh
global'nyh topologii prostranstva
(ploskoe, 
, postoyannoi polozhitel'noi krivizny,
, postoyannoi otricatel'noi krivizny, 
).
- masshtabnyi faktor, edinstvennaya zavisyashaya
ot vremeni velichina.
Zamechanie. Iz vida intervala
=, gde
- elemet koordinatnogo rasstoyaniya, avtomaticheski
poluchaetsya zakon Habbla. Deistvitel'no, kak sleduet iz
zapisi dlya intervala, fizicheskoe rasstoyanie est'
,
t.e. 
. Pust' koordinaty tochek ne menyayutsya,
. Skorost' izmeneniya fizicheskogo
rasstoyaniya tem ne menee ne ravna nulyu
. Integriruya
vdol' geodezicheskoi (t.e. vdol' lucha rasprostraneniya sveta),
poluchaetsya zakon Habbla: 
, gde
- "postoyannaya"
Habbla.
Podstavlyaya etot interval v uravneniya Einshteina,
poluchaem uravneniya Fridmana dlya evolyucii masshtabnogo
faktora. Privedem ih bez vyvoda srazu dlya nenulevoi
kosmologicheskoi postoyannoi 
(kotoraya voobshe govorya mozhet
byt' funkciei vremeni).
Uravnenie energii:
Otmetim, chto vmesto razmernoi velichiny
c
chasto ispol'zuyut bezrazmernuyu
kosmologicheskuyu postoyannuyu, otnesennuyu k kriticheskoi plotnosti
Napomnim, chto sovremennye nablyudeniya ukazyvayut na znachenie
.
Uravnenie (10.12) mozhno perepisat' v vide uravneniya
dvizheniya tochki na poverhnosti sfery radiusa 
(sm. predydushee
rassmotrenie) s massoi 
:
i otrazhaet upominavshiisya
vyshe fakt, chto "davlenie vesit" v OTO.
Iz uravneniya (10.13) sleduet, chto chastica na sfere
ispytyvaet kak deistvie sily prityazheniya polnoi massoi , tak
i silu ottalkivaniya
, kotoraya vyzvana polozhitel'noi
kosmologicheskoi postoyannoi i vozrastaet s rasstoyaniem.
(V teoreticheski dopustimom
sluchae otricatel'noi kosmologicheskoi postoyannoi poyavilas' by dopolnitel'naya
sila "prityazheniya", formal'no pohozhaya na silu, obespechivayushuyu
konfainment kvarkov v adronah).
Znak prostranstvennoi krivizny (t.e. gaussovoi krivizny
3-mernoi giperpoverhnosti postoyannogo vremeni) ne izmenyaetsya
v hode evolyucii Vselennoi, hotya velichina ee, razumeetsya,
zavisit ot vremeni. Gaussova krivizna 3-mernogo prostranstvennogo
secheniya v stacionarnom sluchae opredelyaetsya kak
a pri odnorodnoi deformacii stanovitsya
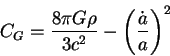
Uchityvaya zakon rasshireniya Habbla
poluchaem
svyaz' znaka krivizny s kriticheskoi plotnost'yu:
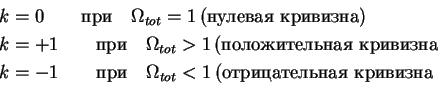
Podcherknem, chto polnaya plotnost' vklyuchaet v sebya i plotnost' vsei materii (vidimoi i nevidimoi), i plotnost' nevidimoi energii (kosmologicheskoi postoyannoi ili kvintessencii)
.
V interesuyushem nas sluchae
dlya pylevidnoi materii
(bez davleniya) est' analiticheskoe reshenie dlya rosta masshtabnogo faktora
) k stadii eksponencial'nogo
rasshireniya
(
).
Krasnoe smeshenie 
, na kotorom proishodit smena rezhima
uskoreniya na zamedlenie, v ploskoi modeli s kosmologicheskoi
postoyannoi (t.e. pri
)
nahoditsya po formule
. Noveishie nablyudatel'nye
dannye po dalekim sverhnovym tipa Ia (samaya dalekaya SN 1997ff
imeet krasnoe smeshenie 
)
svidetel'stvuyut v pol'zu ploskoi modeli s
,
t.e. krasnoe smeshenie, nachinaya s kotorogo Vselennaya rasshiryaetsya
s uskoreniem, okolo
(Ris. 10.6).
 |
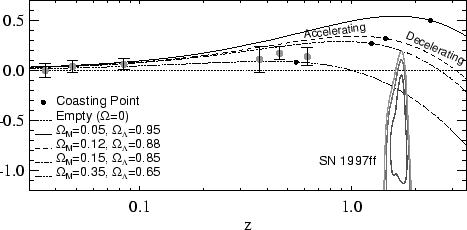Ris. 10.6
Raznica v modulyah rasstoyaniya izvestnyh
kosmologicheskih sverhnovyh Ia v razlichnyh kosmologicheskih modelyah otnositel'no
modeli lineino odnorodno rasshiryayusheisya Vselennoi
("pustaya Vselennaya" s  ) (gorizontal'naya liniya).
Do krasnyh smeshenii  individual'nye sverhnovye usredneny.
Dlya
kazhdoi modeli otmechena tochka (chernyi kvadrat), v kotoroi uskorenie
smenyaetsya zamedleniem. Svet ot samoi dalekoi SN1997ff
byl ispushen v tot moment, kogda Vselennaya rasshiryalas' s
zamedleniem. [Iz raboty
A. Riess et al. 2001, astro-ph/0104455]. |
Podrobnyi kachestvennyi analiz effektov, svyazannyh s polozhitel'noi kosmologicheskoi postoyannoi v FRW-modelyah mozhno naiti v elektronnom preprinte astro-ph/9904398.
<< 10.1 Klassicheskaya kosmologiya | Oglavlenie | 11. Kosmologiya (prodolzhenie) >>
|
Publikacii s klyuchevymi slovami:
zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika
Publikacii so slovami: zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
