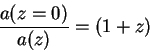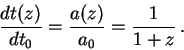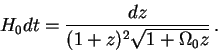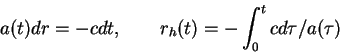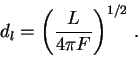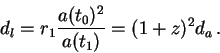---

<< 11. Kosmologiya (prodolzhenie) | Oglavlenie | 11.2 Goryachaya Vselennaya >>

Razdely

• 11.1.1 Gorizont
• 11.1.2 Uglovoe i fotometricheskoe rasstoyaniya
• 11.1.3 Poverhnostnaya yarkost' i paradoks Ol'bersa

---

11.1 Rasprostranenie sveta. Krasnoe smeshenie

Pereidem ot obsuzhdeniya matematicheskih modelei k real'no nablyudaemym velichinam. Osnovnaya informaciya ot kosmicheskih ob'ektov poluchaetsya iz nablyudeniya elektromagnitnyh voln (sveta). Rassmotrim foton chastoty , ispuskaemyi v tochke s koordinatoi na fone rasshiryayusheisya Vselennoi. Pust' priemnik raspolozhen v tochke s koordinatoi .^11.1Skorost' tochki 2 otnositel'no tochki 1 est', ochevidno, . Primenyaya nerelyativistskii effekt Dopplera (t.e. rassmatrivaya ne slishkom udalennye tochki, chto na samom dele okazyvaetsya nesushestvennym), nahodim raznicu mezhdu prinyatoi i ispushennoi chastotoi fotona

Ustremlyaya poluchaem differencial'noe uravnenie

i uchityvaya vyrazhenie postoyannoi Habbla cherez masshtabnyi faktor i integriruya, poluchaem

Analogichno, energiya fotona , umen'shaetsya v hode rasshireniya, temperatura izlucheniya , impul's chastic , dliny voln (v t.ch. de Broilevskaya dlina volny) . Naglyadnaya analogiya rastyazheniyu dlin voln proporcional'no masshtabnomu faktoru imeetsya v zamknutoi Vselennoi, rassmatrivaemoi kak rezonator. Esli est' stoyachaya volna s uzlami, pri adiabaticheskom rasshirenii chislo uzlov dolzhno sohranyat'sya , to est' .

Nablyudaemaya velichina est' krasnoe smeshenie, svyazyvayushee dlinu volny prinimaemogo i ispushennogo fotonov:

Interpretiruya krasnoe smeshenie kak rezul'tat effekta Dopplera, , , Habblovskaya zavisimost' dlya malyh z mozhet byt' zapisana v vide

gde - postoyannaya Habbla, harakterizuyushaya skorost' rasshireniya Vselennoi v nastoyashii moment vremeni, - rasstoyanie do ob'ekta. Primer Habblovskih diagramm dlya sverhnovyh tipa Ia (sm. v Lekcii 10).

Podcherknem eshe raz, chto nablyudaemoi velichinoi v kosmologii yavlyaetsya krasnoe smeshenie v spektrah kakih-libo ob'ektov. Masshtabnyi faktor na krasnom smeshenii svyazan s masshtabnym faktorom nablyudatelya pri kak

(Vselennaya rasshiryaetsya, poetomu v proshlom (t.e. na bol'shih krasnyh smesheniyah) masshtabnyi faktor byl men'she).

Iz  (11.3) takzhe sleduet, chto interval sobstvennogo vremeni (t.e. vremeni, izmerennogo po soputstvuyushim chasam) na krasnom smeshenii izmeryaetsya nablyudatelem kak interval

Iz-za rasshireniya Vselennoi vremya, izmerennoe po chasam segodnyashnego nablyudatelya, v proshlom techet "bystree".

Zavisimosti nablyudaemyh velichin (naprimer, krasnogo smesheniya ot rasstoyaniya) stanovyatsya nelineinymi na bol'shih rasstoyaniyah i trebuyut utochneniya parametrov kosmologicheskoi modeli (polnaya plotnost' veshestva , velichina kosmologicheskoi postoyannoi i t.d.)

Svyaz' vremeni rasprostraneniya sveta do nablyudatelya, nahodyashegosya po opredeleniyu v tochke s , s rasstoyanii, sootvetstvuyushih krasnomu smesheniyu , nahoditsya iz sootnosheniya (11.6) i vo Fridmanovskih modelyah bez kosmologicheskoi postoyannoi osushestvlyaetsya po formule:

Zdes' - polnaya plotnost' v edinicah kriticheskoi, - sovremennoe znachenie postoyannoi Habbla. Zavisimost' vremeni ot krasnogo smesheniya takim obrazom sil'no nelineinaya. Integrirovanie etogo uravneniya po v predelah ot do daet polnoe vremya (nazyvaemoe tzh. Habblovskim vremenem), proshedshee s momenta nachala Fridmanovskogo rasshireniya. Dlya ploskogo mira bez kosmologicheskoi postoyannoi, naprimer, .

Primer: v ploskoi Vselennoi bez kosmologicheskoi postoyannoi ob'ektu na krasnom smeshenii sootvetstvuet vremya s momenta nachala rasshireniya . Dlya poluchaem , t.e. takie ob'ekty obrazovalis' let tomu nazad.

Maksimal'noe krasnoe smeshenie galaktik, izmerennoe po liniyam v ih spektrah, poryadka 5. Fotometricheski izmerennoe krasnoe smeshenie nekotoryh galaktik, obnaruzhennyh v 1998 g. pri glubokom obzore neba s borta kosmicheskogo teleskopa im. Habbla, okolo 10.

11.1.1 Gorizont

Postavim vopros: s kakih rasstoyanii mozhno v principe prinimat' informaciyu v rasshiryayusheisya Vselennoi, inymi slovami, kakov razmer prichinno-svyazannoi oblasti vo Vselennoi? Gorizont sobytii opredelyaetsya kak poverhnost' sfery, obrazovannoi sovokupnost'yu chastic, ispustivshih svet v moment vremeni t = 0, kotoryi prinimaetsya nablyudatelem v moment vremeni . Uravnenie rasprostraneniya sveta v metrike Fridmana-Robertsona-Uokera prinimaet vid (uglovye peremennye )

i uravnenie gorizonta

(postavlen znak minus t.k. luch rasprostranyaetsya ot periferii k centru). Primer. Rassmotrim ploskii mir, , pylevaya stadiya, , , fizicheskii razmer gorizonta v sovremennuyu epohu ; radiacionno-dominirovannaya stadiya , , . Takim obrazom, vo fridmanovskoi kosmologii gorizont vsegda rastet lineino so vremenem , v to vremya kak masshtabnyi faktor rastet bolee medlenno (iz-za zamedlyayushego deistviya gravitacii): , , i rano ili pozdno lyubaya tochka v rasshiryayusheisya Vselennoi okazyvaetsya pod gorizontom, t.e. v prichinno-svyazannoi oblasti. Obratno, uhodya v proshloe zamechaem, chto masshtabnyi faktor v nekotoryi moment rastet bystree gorizonta (v predele , . Eto privodit k odnomu iz paradoksov klassicheskoi kosmologii, kotoryi reshaetsya v modeli inflyacionnoi Vselennoi (sm. Lekciyu 12).

11.1.2 Uglovoe i fotometricheskoe rasstoyaniya

Ponyatie rasstoyaniya v rasshiryayusheisya Vselennoi, opisyvaemoi metrikoi Fridmana-Robertsona-Uokera, trebuet poyasneniya. Tak, ego mozhno opredelyat' po uglovomu razmeru istochnika so standartnymi razmerami (uglovoe rasstoyanie), ili po prinimaemomu ot standartnogo istochnika potoku izlucheniya (fotometricheskoe rasstoyanie), ili po sobstvennomu dvizheniyu istochnika so standartnoi skorost'yu (metricheskoe rasstoyanie). Ochevidno, v ploskom prostranstve-vremeni vse tri sposoba dadut odin i tot zhe rezul'tat. No Vselennaya opisyvaetsya iskrivlennym prostranstvom-vremenem (dazhe esli trehmernoe prostranstvo evklidovo!) s izmenyayushimsya masshtabnym faktorom, poetomu ukazannye sposoby dadut sushestvenno razlichnye znacheniya uzhe pri .

11.1.2.1 Uglovoe rasstoyanie

V evklidovoi geometrii opredelim uglovoe rasstoyanie kak rasstoyanie, vychislyaemoe po vidimomu uglovomu razmeru ob'ekta : , gde - sobstvennyi razmer ob'ekta perpendikulyarno k luchu zreniya. Pust' svet byl ispushen v moment vremeni (eto vremya zadaetsya usloviem, chto svet prinimaetsya segodnya, t.e. pri , na ), a koordinata ob'ekta byla (NB: koordinata ob'ekta ne izmenyaetsya v hode kosmologicheskogo rasshireniya!). Sobstvennoe rasstoyanie poluchaetsya iz sootnosheniya dlya intervala pri : . Bez poteri obshnosti polagaem . Schitaya ugol malym, iz elementa metriki nahodim , i t.o.

ili s uchetom svyazi ( - krasnoe smeshenie, sootvetstvuyushee vremeni ispuskaniya signala )

Velichina takzhe imeet razmernost' rasstoyaniya i smysl "metricheskogo rasstoyaniya" do istochnika s koordinatoi v moment priema signala.

Iz etih rassuzhdenii takzhe poluchaem zavisimost' ugla, pod kotorym viden istochnik s sobstvennym razmerom , ot krasnogo smesheniya

Otmetim, chto vblizi gorizonta , , , , t.e. ugol , pod kotorym viden udalyayushiisya ob'ekt konechnyh razmerov, v rasshiryayusheisya Vselennoi s lyuboi geometriei dolzhen prohodit' cherez minimum. Naglyadnaya analogiya sushestvuet v zamknutom mire s postoyannnoi polozhitel'noi kriviznoi s topologiei poverhnosti sfery. Tam minimum dostigaetsya na "ekvatore" nablyudatelya.

11.1.2.2 Fotometricheskoe rasstoyanie

Mozhno opredelit' rasstoyanie do ob'ekta i po-drugomu: pust' ob'ekt imeet postoyannuyu sobstvennuyu svetimost' , a prinimaemyi potok izlucheniya ot nego . Polozhim po opredeleniyu fotometricheskoe rasstoyanie do ob'ekta

V rasshiryayusheisya Vselennoi

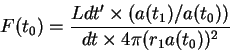
otkuda, ispol'zuya svyaz'  (11.6), poluchaem

Mozhno predlozhit' bolee fizicheskii vyvod etogo sootnosheniya. Potok izlucheniya ot nekotorogo istochnika umen'shaetsya iz-za geometricheskogo faktora, tak kak raspredelyaetsya po poverhnosti sfery , no iz-za rasshireniya Vselennoi poyavletsya eshe i dopolnitel'naya zavisimost' ot krasnogo smesheniya . Odna stepen' poluchaetsya iz-za pokrasneniya fotona (umen'shenie ego chastoty, sobstvenno krasnoe smeshenie), eshe odna stepen' - za schet umen'sheniya chastoty prihoda otdel'nyh fotonov (rastyazhenie vremeni). V itoge poluchaem dlya integral'nogo potoka

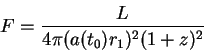
i takim obrazom po opredeleniyu .

Obratite vnimanie, chto na gorizonte , no teper' ! V otlichie ot uglovogo rasstoyaniya, fotometricheskoe rasstoyanie monotonno rastet s krasnym smesheniem.

11.1.3 Poverhnostnaya yarkost' i paradoks Ol'bersa

Poverhnostnuyu yarkost' istochnika mozhno opredelit' kak potok izlucheniya, prinimaemyi detektorom ot vsego istochnika, otnesennyi k telesnomu uglu, kotoryi zanimet istochnik na nebe. Po suti dela eto est' ne chto inoe, kak intensivnost' izlucheniya (sm. Lekciyu 2). V Evklidovoi geometrii telesnyi ugol menyaetsya s udaleniem ot istochnika kak , potok takzhe umen'shaetsya s rasstoyaniem kak , t.e. poverhnostnaya yarkost' dolzhna ostavat'sya postoyannoi (teorema o sohranenii intensivnosti vdol' lucha zreniya). Kakova situaciya v rasshiryayusheisya Vselennoi? Vyshe my pokazali, chto lineinyi ugol , t.e. telesnyi ugol . Integral'nyi zhe potok izlucheniya , otkuda poluchaem

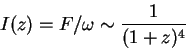
[Eto sootnoshenie bolee formal'no mozhno poluchit' iz Lorenc-invariantnosti velichiny ].

Vazhnoe prakticheskoe primenenie etoi formuly sostoit v ob'yasnenii znamenitogo paradoksa Ol'bersa (XIXv), soglasno kotoromu v beskonechnoi Vselennoi, zapolnennoi zvezdami, rano ili pozdno dolzhen nastupit' moment, kogda vse nebo polnost'yu perekryvaetsya diskami zvezd. Eto protivorechit izvestnomu faktu, chto noch'yu nebo temnoe. Razreshenie etogo paradoksa v ramkah modeli rasshiryayusheitsya Vselennoi trivial'no - svecheniya neba ne nastupaet iz-za znachitel'nogo oslableniya intensivnosti s krasnym smesheniem. K tomu zhe zvezd i galaktik ne bylo na bol'shih krasnyh smesheniyah (pervye zvezdy obrazovalis' iz-za gravitacionnoi neustoichivosti pri ), i perekrytiya neba diskami tozhe zvezd net.

---

<< 11. Kosmologiya (prodolzhenie) | Oglavlenie | 11.2 Goryachaya Vselennaya >>

Publikacii s klyuchevymi slovami: zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika Publikacii so slovami: zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika
Sm. takzhe: Mestnoe mezhzvezdnoe oblako Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Razlozhenie dalekogo sveta Sravnenie razmerov zvezd Vse publikacii na tu zhe temu >>