---

<< 14. GV astronomiya | Oglavlenie | 14.2 Detektirovanie GV >>

14.1 Opisanie

Soglasno teorii gravitacii A.Einshteina (obshei teorii otnositel'nosti, OTO), lyubaya plotnost' energii mozhet byt' opisana v terminah gravitacionnogo polya, a samo gravitacionnoe pole naglyadno predstavlyaetsya kak iskrivlenie prostranstva-vremeni, v kotorom nahoditsya materiya^14.2. Iskrivlenie oznachaet, chto kvadrat intervala mezhdu dvumya sobytiyami v prisutstvii materii otlichaetsya ot kvadrata intervala v special'noi teorii otnositel'nosti , a imenno, pered kvadratom elementa vremeni i dliny poyavlyayutsya koefficienty, zavisyashie ot koordinat i vremeni. 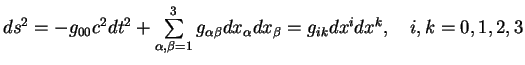V obshem sluchae mozhno zapisat' (po povtoryayushimsya indeksam podrazumevaetsya summirovanie, vremya schitaetsya koordinatoi s nulevym indeksom). Kvadratnaya simmetrichnaya matrica nazyvaetsya metrikoi prostranstva-vremeni. T.o. v obshem sluchae imeetsya 10 nezavisimyh velichin , kotorymi harakterizuetsya gravitacionnoe pole. Napomnim, chto v N'yutonovskoi gravitacii dostatochno odnogo skalyarnogo gravitacionnogo potenciala , vychislyaemogo iz prostranstvennogo raspredeleniya plotnosti s pomosh'yu uravneniya Puassona .

Fizicheskii smysl koefficientov metriki yasen iz ih vida v priblizhenii slabogo polya^14.3: dlya sfericheski-simmetrichnogo nevrashayushegosya tela , . Sila, deistvuyushaya na probnye tela (napryazhennost' gravitacionnogo polya) opredelyaetsya gradientom potenciala v N'yutonovskoi teorii i v obshem sluchae - proizvodnymi metriki po koordinatam i vremeni.

V obychnyh zemnyh usloviyah metrika ochen' malo otlichaetsya ot metriki pustogo prostranstva (t.n. metriki Minkovskogo) ^14.4. Dlya slabogo gravitacionnogo polya mozhno linearizovat' metriku, zapisav , gde - maloe vozmushenie koordinat i vremeni. Linearizaciya uravnenii OTO bez istochnika polya v pravoi chasti privodit k volnovomu uravneniyu ( - operator D'Alambera), kotoroe opisyvaet rasprostranenie volny so skorost'yu sveta v pustom prostranstve.

Do serediny 60-h godov shli teoreticheskie spory, predstavlyayut li gravitacionnye volny fizicheskuyu real'nost' ili oni yavlyayutsya matematicheskoi fikciei. Odnako v nastoyashee vremya dokazano, chto gravitacionnye volny perenosyat energiyu i impul's, kotorye mogut peredavat' makroskopicheskim telam. Obrazno mozhno predstavit' sebe gravitacionnuyu volnu kak melkuyu "ryab'" na poverhnosti okeana, prichem bol'shoi radius krivizny okeana predstavlyaet soboi fonovuyu kriviznu prostranstva-vremeni, na kotoroi rasprostranyayutsya volny, a vzaimodeistvie s makroskopicheskimi telami - kak kachanie "lodki" na etoi ryabi. ^14.5

Obychno rassmatrivayut ploskie volny (chto vpolne opravdano dlya udalennyh istochnikov) i dlya opisaniya ih vzaimodeistviya s makroskopicheskimi telami vybirayut special'nuyu sistemu koordinat, v kotoroi opisanie vzaimodeistviya GV s makroskopicheskimi telami priobretaet naibolee prostoi vid (yasno, chto vybor sistemy koordinat ne dolzhen skazyvat'sya na fizicheskih effektah). Fiksaciya sistemy koordinat v chetyrehmernom prostranstve-vremeni nakladyvaet 8 dopolnitel'nyh uslovii, i togda iz 10 nezavisimyh velichin real'no nezavisimymi okazyvayutsya tol'ko dve, kotorye nazyvayut i polyarizacimi (prinyaty oboznacheniya ) v sootvetstvii s tem, kak deistvuyut eti volny na probnye tela (sm. 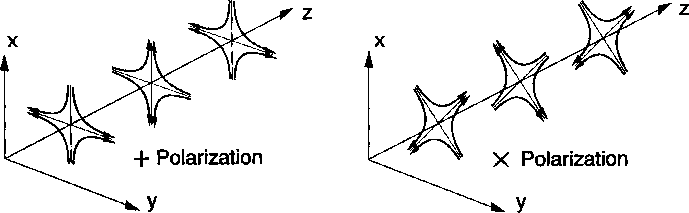Ris. 14.1).

Podobno tomu, kak zaryazhennaya chastica v pole ploskoi elektromagnitnoi volny nachinaet sovershat' kolebaniya, vzaimodeistvie gravitacionnoi volny s makroskopicheskimi telami privodit k poyavleniyu otnositel'nyh uskorenii i k izmeneniyu fizicheskogo rasstoyaniya mezhdu nimi. Naprimer, otnositel'noe izmenenie rasstoyaniya mezhdu dvumya probnymi telami v pole ploskoi GV

gde - lineinaya kombinaciya plyus- i kross- polyarizacii GV, zavisyashaya ot orientacii tel otnositel'no napravleniya rasprostraneniya volny. Eto sootnoshenie naglyadno pokazyvaet, chto po svoemu fizicheskomu smyslu amplituda GV yavlyaetsya bezrazmernoi velichinoi. Chasto ee nazyvayut "bezrazmernoi amplitudoi vozmushenii metriki", sozdavaemyh prohodyashei GV.

---

<< 14. GV astronomiya | Oglavlenie | 14.2 Detektirovanie GV >>

Publikacii s klyuchevymi slovami: zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika Publikacii so slovami: zvezdy - Mezhzvezdnaya sreda - Kosmologiya - teoreticheskaya astrofizika - astrofizika
Sm. takzhe: Mestnoe mezhzvezdnoe oblako Chernaya dyra razrushaet zvezdu: animaciya Zvezdy, pyl' i tumannost' v NGC 6559 25 samyh yarkih zvezd na nochnom nebe Animaciya: chernaya dyra razrushaet zvezdu Razlozhenie dalekogo sveta Sravnenie razmerov zvezd Vse publikacii na tu zhe temu >>