Zvezdy: ih stroenie, zhizn' i smert'| predydushaya |
sleduyushaya
|
Vektornoe uravnenie vtorogo poryadka v samosopryazhennom vide
V nekotoryh sluchayah uravnenie gidrostaticheskogo ravnovesiya vmeste s uravneniem
dlya gravitacionnogo potenciala mozhno privesti k vektornomu uravneniyu vtorogo
poryadka dlya odnoi neizvestnoi. Estestvenno, chto eto vozmozhno prinalichii nekotoroi
dopolnitel'noi informacii (uravneniya), pozvolyayushei isklyuchit' odnu iz neizvestnyh
velichin. Naprimer, polozhim, davlenie est' izvestnaya funkciya plotnosti P(
)
. Eto, konechno ne verno v obshem sluchae, odnako dazhe kogda eto ne tak, poluchennoe
nami uravnenie mozhet byt' polezno v lokal'nom analize - v okrestnosti lyuboi
tochki modeli mozhno approksimirovat' povedenie davleniya nekotoroi funkciei tol'ko
plotnosti.
Vozvrashayas' k nashim uravneniya, zametim, chto udobnoi formoi moglo byt' uravnenie Puassona - s neizvestnoi v vide potenciala i standartnym vidom differencial'nogo operatora Laplasa. V etom sluchae nam ostalos' naiti podhodyashee vyrazhenie plotnosti cherez potencial, naprimer v vide
(to est' my ishem funkciyu f, takuyu chto 
=f()).
Dlya ee nahozhdeniya nuzhno vspomnit' o uravnenii gidrostaticheskogo ravnovesiya,
v vektornoi forme. Po nashim predpolozheniyam,
davlenie est' funkciya plotnosti, poetomu sleva est' nekotoraya funkciya plotnosti.
Esli by udalos' etu funkciyu plotnosti vyrazit' kak gradient nekotoroi drugoi
funkcii plotnosti, to posle integrirovaniya my poluchili by interesuyushuyu nas zamenu.
Drugimi slovami, nuzhno reshit' uravnenie vida
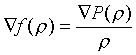
otnositel'no neizvestnoi funkcii f, schitaya nezavisimoi
peremennoi . Formal'noe reshenie ochevidno imeet vid
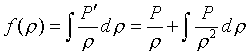
(vtoroe ravenstvo est' prosto integrirovanie po chastyam). Takim obrazom, ispol'zuya poluchennuyu nami funkciyu f, mozhno zapisat' vektornoe uravnenie vtorogo poryadka dlya potenciala v vide
Dannoe uravnenie spravedlivo v prostranstve lyuboi razmernosti, i v koordinatah s lyuboi simmetriei (sfericheskie, cilindricheskie i t.d.)
Primer primeneniya dlya politropnyh konfiguracii
Istoricheski naibolee izvestnym sluchaem ispol'zovaniya uproshennyh predpolozhenii
pri postroenii modelei zvezd yavlyaetsya sluchai politropnyh zvezd, to est' sluchai
P=K
. Togda iskomaya funkciya, svyazyvayushaya
potencial i plotnost', imeet vid
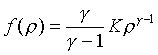
a obshee uravnenie dlya politropnoi konfiguracii imeet vid (s ispol'zovaniem masshtabiruemogo radiusa dlya privedeniya k bezrazmernomu vidu)
ili s uchetom sfericheskoi simmetrii, v vide uravneniya vtorogo poryadka
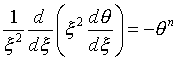
(zdes' 
i 
- bezrazmernye potencial i radius).
V sluchae izotermicheskoi konfiguracii, kogda P=K,
uravnenie perehodit v
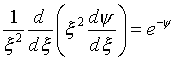
Otmetim, chto izotermicheskie konfiguracii imeyut beskonechnuyu protyazhennost', i neogranichennuyu potencial'nuyu energiyu. Poetomu poslednee uravnenie mozhet imet' smysl tol'ko kak lokal'noe.
V.Baturin
| predydushaya |
sleduyushaya
|
|
Publikacii s klyuchevymi slovami:
Sverhnovye - zvezdy - sverhgigant - neitronnye zvezdy - krasnyi gigant - buryi karlik - diagramma Gercshprunga-Ressela - belyi karlik - Evolyuciya zvezd - termoyadernye reakcii - vyrozhdennyi gaz - gidrostaticheskoe ravnovesie - konvekciya - luchistyi perenos - glavnaya posledovatel'nost' - evolyucionnyi trek zvezdy - karliki
Publikacii so slovami: Sverhnovye - zvezdy - sverhgigant - neitronnye zvezdy - krasnyi gigant - buryi karlik - diagramma Gercshprunga-Ressela - belyi karlik - Evolyuciya zvezd - termoyadernye reakcii - vyrozhdennyi gaz - gidrostaticheskoe ravnovesie - konvekciya - luchistyi perenos - glavnaya posledovatel'nost' - evolyucionnyi trek zvezdy - karliki | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
