Zvezdy: ih stroenie, zhizn' i smert'

---

	vverh
predydushaya	oglavlenie	sleduyushaya

---

Statisticheskaya model' ideal'nogo gaza

Izlozhim kachestvenno nekotorye predstavleniya statisticheskoi fiziki na primere ideal'nogo gaza. Hotya bol'shinstvo predpolozhenii mogut i ne ispol'zovat'sya pri analize termodinamiki ideal'nogo gaza, no vo-pervyh, eti predpolozheniya aktual'ny pri rassmotrenii bolee slozhnyh sluchaev, a vo-vtoryh, ispol'zovoe obshego statisticheskogo opisaniya pozvolyaet vsecelo opredelit' ideal'nyi gaz, vklyuchaya ego entropiyu, i vse neobhodimye raspredeleniya (po skorostyam ili flyuktuacii srednih velichin).

Sushestvuyut dva osnovnyh metoda dlya opisaniya raspredelenii v statisticheskoi fizike. Odno, eto raspredelenie Gibbsa (ili bol'shoe kanonicheskoe raspredelenie) i vtoroe, eto raspredelenie Maksvella-Bol'cmana (ili mikrokanonicheskoe raspredelenie). Nesmotrya na to, chto raspredelenie Gibbsa v nekotorom smysle bolee obshee, naglyadno predstavlyat' legche vtoroi tip, to est' mikrokanonicheskoe raspredelenie. Poetomu my nachnem so vtorogo.

Prezhde chem pereiti k opisaniyu raspredelenni, otmetim obshuyu chertu (tochnee, osnovnoi princip) dlya oboih tipov. Etot princip sostoit v tom, chto veroyatnost' sistemy (ili ob'ekta) nahodit'sya v sostoyanii i (chto eto za ob'ekty i sostoyaniya - zavisit ot tipa raspredeleniya) proporcional'na e^-E_i/kT, gde E_i - energiya etogo sostoyaniya.

Neskol'ko v shutochnoi forme mozhno skazat', chto situaciya podobna sluchainomu razmesheniyu knig na stelazhah slozhnoi formy. Kazhdoe mesto, kuda kniga mozhet byt' postavlena, eto sostoyanie i, a vysota polki, na kotoroi my ishem knigu - eto ee energiya. Togda dlya kazhdoi knigi mozhno sopostavit' "temperaturu", harakterizuyushuyu to, kak chasto etu knigu brali i stavili na mesto. A veroyatnost' naiti knigu na vysokih polkah (pri umerennyh "temperaturah") sushestvenno men'she, chem na samyh vysokih. Pri etom forma stelazha i kolichestvo mest na kazhdoi polke mozhet byt' ochen' raznym - imenno eto harakterizuet konkretnuyu sistemu.

Vernemsya k mikrokanonicheskomu raspredtleniyu i opishem "stelazhi". V nachale, ne budem vspominat' o kvantovyh effektah, tak skazat', chisto klassicheskoe opisanie. V osnove lezhit predstavlenie o fazovom prostranstve ili ego eshe nazyvayut - prostranstvom dlya odnoi chasticy. Esli rassmatrivat' chasticu iz ideal'nogo gaza, ee fazovoe prostranstvo 6-mernoe, i sostoit iz 3-h koordinatnyh i 3-h impul'snyh osei. Chastica, v obshem sluchae, mozhet zanimat' lyuboe polozhenie v etom prostranstve, ogranichennoe po koordinatnym osyam razmerami sistemy. Poskol'ku my ne predpolagaem nikakih vneshnih sil (sil tyazhesti, magnitnyh polei i t.p.), to energiya chasticy ne zavisit ot polozheniya v prostranstve, i veroyatnosti vseh dostupnyh polozhenii v prostransvennyh koordinatah odinakovy. Tem samym my sposobny narisovat' osi impul'sov iz fazovogo prostranstva, i operirovat' s nimi v dal'neishem. Energiya chasticy opredelyaetsya kvadratom impul'sa i massoi, to est' v prostranstve impul'sov vse sfericheskie "stelazhi" imeyut odinakovye energii (nahodyatsya na odinakovoi "vysote"). Odnako ob'emy etih stelazhei ne odinakovy - oni proporcional'ny ob'emam sharovyh sloev so srednim radiusom p. Ob'em etogo sloya ochevidno raven 4p²dp. Vse polozheniya vnutri etogo sloya ravnoveroyatny, tak chto esli my interesuemsya raspredlenie po impul'sam (tozhe, chto po energiyam), to poluchim, chto veroyatnost' w(p) ravna

V etoi formule nachal'naya konstanta imeet smysl normirovki plotnosti veroyatnosti, to est' nahoditsya iz usloviya, w(p)dp=1. Etu formulu legko perepisat' v vide raspredeleniya skorostei chastic, to est'

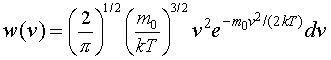
horosho izvestnoe raspredelenie Maksvella dlya skorostei chastic v ideal'nom gaze. Legko ponyat', chto mozhno ispol'zovat' eto poluchennoe raspredelenie dlya vyvoda makroskopicheskogo davleniya, v mehanicheskom smysle. Edistvennoe, chto dlya etogo nuzhno, eto ubedit'sya, chto srednyaya energiya chastic E=w(E)dE ostaetsya ravnoi 3kT/2.

Uprazhnenie. Pokazhite, chto naibolee veroyatnaya skorost' chastic ravna (2kT/m₀)^1/2, srednyaya skorost' ravna (8kT/m₀)^1/2, a srednekvadratichnaya skorost' ravna (3kT/m₀)^1/2.

Vernemsya k konstante normirovki v raspredelenii impul'sov (2m₀kT)^-1/2. Eta velichina smysl srednego impul'sa chastic pri rassmatrivaemom raspredelenii.

V.Baturin

---

predydushaya

v nachalo

sleduyushaya

 

Publikacii s klyuchevymi slovami: Sverhnovye - zvezdy - sverhgigant - neitronnye zvezdy - krasnyi gigant - buryi karlik - diagramma Gercshprunga-Ressela - belyi karlik - Evolyuciya zvezd - termoyadernye reakcii - vyrozhdennyi gaz - gidrostaticheskoe ravnovesie - konvekciya - luchistyi perenos - glavnaya posledovatel'nost' - evolyucionnyi trek zvezdy - karliki Publikacii so slovami: Sverhnovye - zvezdy - sverhgigant - neitronnye zvezdy - krasnyi gigant - buryi karlik - diagramma Gercshprunga-Ressela - belyi karlik - Evolyuciya zvezd - termoyadernye reakcii - vyrozhdennyi gaz - gidrostaticheskoe ravnovesie - konvekciya - luchistyi perenos - glavnaya posledovatel'nost' - evolyucionnyi trek zvezdy - karliki

Sm. takzhe: Chernaya dyra razrushaet zvezdu: animaciya NGC 2440: kokon novogo belogo karlika μ Cefeya NGC 1097: spiral'naya galaktika so sverhnovoi Zvezdy, pyl' i tumannost' v NGC 6559 Obrechennaya zvezda η Kilya Pererabotka veshestva v Kassiopee A Vse publikacii na tu zhe temu >>