Astronet > 2.3 Obobshennaya procedura Belinfante. Nezavisimost' obobshennyh zakonov sohraneniya ot divergencii v lagranzhianah

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 2.2 Prilozhenie procedury Belinfante ... | Oglavlenie | Literatura k Lekcii 2 >>

Razdely

2.3 Obobshennaya procedura Belinfante. Nezavisimost' obobshennyh zakonov sohraneniya ot divergencii v lagranzhianah

Napomnim, chto v lekcii 1 procedura Neter byla prilozhena k obshego vida teorii s lagranzhianom $\hat L = \hat L (A_B; A_{B,\alpha}; A_{B,\alpha\beta})$ , kotoryi byl ,,kovariantizovan'' vvedeniem vneshnei fonovoi metriki $\bar g_{\mu\nu}$ i priveden k vidu

$\begin{displaymath} \hat L = {\hat{\cal L}}_c = {{\hat{\cal L}}}_c (A_B; \overline D_\alpha A_{B}; \overline D_\beta \overline D_\alpha A_{B}). \end{displaymath}$

(2.30)

Byl poluchen zakon sohraneniya

$\begin{displaymath} \hat i^\alpha \equiv \overline D_\tau \hat \Phi^{\alpha\tau}(\xi) \end{displaymath}$

(2.31)

s tokom i superpotencialom opredelennymi v lekcii 1:

$\displaystyle \hat i^\alpha$	$\textstyle \equiv$	$\displaystyle -\left[\left(\hat u^{\alpha}_\sigma + \hat n^{\alpha\tau\beta}_\l... ...\alpha\tau}_{\sigma}\overline D_\tau \xi^\sigma + \hat Z^{\alpha}_{(1)}\right],$
$\displaystyle \hat \Phi^{\alpha\tau} (\xi)$	$\textstyle \equiv$	$\displaystyle \left(\hat m^{\tau\alpha}_\sigma + \overline D_\lambda \hat n^{\l... ...{4\over 3}} \hat n^{[\alpha\tau]\lambda}_\sigma \overline D_\lambda \xi^\sigma,$

koefficienty v kotoryh opredeleny v formulah (39) - (41) lekcii 1. Opredelyaem popravku Belinfante po standartnym pravilam (2.17)

$\begin{displaymath} \hat S^{\mu\nu\rho} \equiv - \hat m^{\rho[\mu}_\lambda \bar ... ...{\nu]\lambda} + \hat m^{\nu[\rho}_\lambda \bar g^{\mu]\lambda} \end{displaymath}$

(2.32)

i dobavlyaem k obeim chastyam 2.31) velichinu $\overline D_\tau \left(\hat S^{\alpha\tau\rho}\xi_{\rho}\right)$ . Poluchim obobshennyi zakon sohraneniya, sootvetstvuyushii kombinacii procedur Neter i Belinfante:

$\begin{displaymath} \hat i^\alpha_{NB} \equiv \overline D_\tau \hat \Phi^{\alpha\tau}_{NB}(\xi). \end{displaymath}$

(2.33)

Teper' skorrektirovannyi tok priobretaet vid:

$\begin{displaymath} \hat i^\alpha_{NB} \equiv -\left[ \left(\hat u^{\alpha}_\sig... ...}_{ \sigma}\right) \xi^\sigma+ \hat Z^{\alpha}_{(2)}\right], \end{displaymath}$

(2.34)

a skorrektirovannyi superpotencial:

$\begin{displaymath} \hat \Phi^{\alpha\tau}_{NB} (\xi) \equiv 2\left[\overline D_... ...t n^{[\alpha\tau]\lambda}_\sigma\overline D_\lambda\xi^\sigma. \end{displaymath}$

(2.35)

2.3.1 Svoistva novyh zakonov sohraneniya i novyh skorrektirovannyh velichin

(a) Kak i dolzhno byt' v silu opredeleniya procedury Belinfante, tok (2.34) ne soderzhit yavno spinovogo chlena. Zakony sohraneniya teper' opredelyayutsya edinym oboshennym ,,simmetrizovannym'' tenzorom energii-impul'sa


		$\displaystyle \hat {\cal T}_{(NB)\sigma}^\alpha = - \left(\hat u^{\alpha}_\sigm... ...mbda_{ \tau\beta\sigma} - \overline D_\nu \hat S^{\alpha\nu}_{ \sigma}\right).$

Z-chlen, kak i prezhde, obrashaetsya v nul' na killingovyh vektorah fona.

(b) V voprose ob edinstvennosti vse te utverzhdeniya, kotorye byli sdelany otnositel'no obobshennyh tokov i superpotencialov $\hat i^\alpha$ and $\hat \Phi^{\alpha\tau}$ v lekcii 1 ostayutsya v sile. Popravka Belinfante (2.32) takzhe opredelena odnoznachno lagranzhianom (2.30).

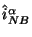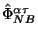Takim obrazom, my utverzhdaem, chto $\hat i^\alpha_{NB}$ i $\hat \Phi^{\alpha\tau}_{NB}$ edinstvennym obrazom v smysle procedury Neter-Belinfante opredelyayutsya lagranzhianom modeli.

Etot vyvod vazhen dlya nas po sleduyushei prichine. Podstanovka v formuly (2.32) - (2.35) konkretnogo lagranzhiana KBL ( ${\hat{\cal L}}_G$ v (2.20)) daet tochno te rezul'taty, kotorye predlozheny v predydushei chasti. A eto oznachaet, chto punkt (ii) v proshloi chasti etoi lekcii podtverzhdaetsya, to est' rezul'taty [10] $^{\!- }$ [12], odnoznachny v smysle procedury Neter-Belinfante.

(c) Zametim, chto superpotencial (2.35) zavisit tol'ko ot n-koefficientov. Eto horosho sootnositsya s izvestnymi faktami. Naprimer, bolee prostaya teoriya s lagranzhianom (2.9) ne soderzhit n-koefficientov -- rezul'tat takoi, chto posle prilozheniya metoda Belinfante skorretirovannyi superpotencial v (2.18) obrashaetsya v nul'. V bolee slozhnoi modeli Mollera [16], gde OTO predstavlena s pomosh'yu tetrad, no bez vtoryh proizvodnyh v kovariantnom lagranzhiane, takzhe otsutstvuyut n-koefficienty. Rezul'tat tot zhe: Belinfante popravka daet nulevoi superpotencial. V etom smysle model' s KBL lagranzhianom bolee predpochtitel'na: ona privodit k superpotencialu tipa (2.35), kotoryi privodit k zakonam sohraneniya udovletvoryayushim vsem estestvennym testam.

2.3.2 Nezavisimost' ot divergencii v lagranzhiane

Napomnim, chto vklady v tok i superpotencial (poluchennye metodom Neter) ot divergencii v lagranzhiane: $\Delta_{(div)} \hat L = \partial_\nu \hat k^\nu$ sootvetstvuyut formulam:

		$\displaystyle \hat i^\alpha +\Delta_{(div)} \hat i^\alpha$
		$\displaystyle = - \left(\hat u^{\alpha}_\sigma + \Delta_{(div)} \hat u^{\alpha}... ...^{\alpha\tau}_{\sigma}\right) \overline D_\tau \xi^\sigma - \hat Z^\alpha_{(1)}$
		$\displaystyle \equiv \overline D_\tau \left[\hat \Phi^{\alpha\tau} + \Delta_{(div)} \hat \Phi^{\alpha\tau}(\xi)\right],$	(2.36)

gde

$\displaystyle \Delta_{(div)}\hat u^\alpha_\sigma$	=	$\displaystyle 2 \overline D_\tau\left(\delta^{[\alpha}_\sigma \hat k^{\tau]} \right),$
$\displaystyle \Delta_{(div)}\hat m^{\alpha\tau}_\sigma$	=	$\displaystyle 2 \left(\delta^{[\alpha}_\sigma \hat k^{\tau]} \right),$
$\displaystyle \Delta_{(div)}\hat \Phi^{\alpha\tau}$	=	$\displaystyle -2 \left(\xi^{[\alpha} \hat k^{\tau]} \right).$	(2.37)

Popravka Belinfante (2.32) dlya dobavki $\Delta_{(div)} \hat m^{\alpha\tau}_{\sigma}$ imeet takzhe prostuyu formu:

$\begin{displaymath} \Delta_{(div)} \hat S^{\alpha\tau\rho}\xi_\rho = 2\xi^{[\alpha}\hat k^{\tau]}. \end{displaymath}$

(2.38)

Primenim Belinfante metod k (2.36). V silu opredeleniya procedury ischeznet spinovyi chlen. A v silu znachenii (2.37) i (2.38) ischeznut i sovmestnye popravki:

$\Delta_{(div)} \hat u^{\alpha}_\sigma - \overline D_\tau \left(\Delta_{(div)} \hat S^{\alpha\tau\rho}\bar g_{\rho\sigma}\right)\equiv 0,$

$\Delta_{(div)} \hat S^{\alpha\tau\rho}\xi_\rho + \Delta_{(div)} \hat \Phi^{\alpha\tau}\equiv 0$ .

Takim obrazom, kombinirovannaya procedura Neter-Belinfante privodit k divegentno nezavisimym velichinam v zakonah sohraneniya. Inache, forma sohranyayushihsya toka i superpotenciala ne zavisyat ot granichnyh uslovii pri var'irovanii lagranzhiana.

Etot rezul'tat podtverzhdaet punkt (ix) proshloi chasti etoi lekcii. V rabote [17] uzhe bylo otmecheno, chto metod Belinfante, primenennyi kak k usechennomu lagranzhianu Einshteina, tak i lagranzhianu Gilberta daet odin i tot zhe rezul'tat. Fakticheski my obobshaem etot rezul'tat na proizvol'nye teorii s proizvol'no iskrivlennymi fonami. Rezul'taty etoi chasti dolozheny na seminare [18].

<< 2.2 Prilozhenie procedury Belinfante ... | Oglavlenie | Literatura k Lekcii 2 >>

Publikacii s klyuchevymi slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Sm. takzhe: Padenie shara v Solnechnoi sisteme Gravitacionnye anomalii na Merkurii Galaktika Arp 94 Sputniki GRAIL sostavlyayut kartu lunnoi gravitacii 70 let Stivenu Hokingu Molotok protiv peryshka na Lune Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce