Astronet > 3.3 Zakony sohraneniya i integral'nye velichiny dlya vozmushennoi fridmanovskoi modeli

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 3.2 Konformnye vektory Killinga dlya ... | Oglavlenie | 3.4 Novye integral'nye sootnosheniya >>

Razdely

3.3 Zakony sohraneniya i integral'nye velichiny dlya vozmushennoi fridmanovskoi modeli

Kvazi-lokal'nye, ili global'no sohranyayushiesya velichiny ves'ma interesny v kosmologii, i obychno raschityvayutsya vnutri sfery na secheniyah postoyannogo vremeni $\eta$ . Chtoby ih poluchit' obychno ispol'zuetsya differencial'nyi zakon sohraneniya tipa (2.24) v lekcii 2: $\hat {\cal I}^\mu=\partial_\nu\hat{\cal I}^{\mu\nu}$ , kotoryi zdes' (v lineinom priblizhenii po vozmusheniyam) my ispol'zuem, tochnee, ego nulevuyu komponentu:

$\begin{displaymath} \hat {\cal I}^0=\partial_l\hat{\cal I}^{0l}. \end{displaymath}$

(3.16)

3.3.1 Vozmushennoe fridmanovskoe reshenie i lineinye priblizheniya

Oboznachim vozmushennuyu metriku (3.1) kak eto bolee prinyato $g_{\mu\nu}=a^2(e_{\mu\nu}+{\tilde h}_{\mu\nu})$ . Takim obrazom imeem

$\begin{displaymath} ds^2= a^2(e_{\mu\nu}+{\tilde h}_{\mu\nu})dx^\mu dx^\nu. \end{displaymath}$

(3.17)

Krome togo, my ispol'zuem 3-mernye komponenty: ${\tilde h}_{00}, {\tilde h}_{0l}, {\tilde h}_{kl}$ , indeksy kotoryh podnimayutsya i opuskayutsya s pomosh'yu f_kl:

$\begin{displaymath} {\tilde h}^m_l=f^{mk}{\tilde h}_{kl}, {\tilde h}^{mn}=f^{mk}f^{nl}{\tilde h}_{kl}, {\tilde h}^m_0=f^{ml}{\tilde h}_{0l}. \end{displaymath}$

(3.18)

V modeli, razvitoi v lekcii 2 ispol'zuyutsya vozmusheniya $\hat l^{\mu\nu} = \hat g^{\mu\nu} -\bar {\hat g^{\mu\nu}}$ . Kak bylo otmecheno, preimushestvo etogo v tom, chto model', v principe, mozhet byt' legko proschitana do lyubogo poryadka po vozmusheniyam, poskol'ku v terminah $\hat l^{\mu\nu}$ my predstavlyaem tochnye uravneniya i tochnyi, hotya i v lineinoi forme superpotencial. Zdes' my ogranichivaemsya lish' lineinymi priblizheniyami i ispol'zuem bolee populyarnuyu formu vozmushenii ${\tilde h}_{\mu\nu}$ . Poetomu zdes' formuly lekcii 2 my pereschityvaem v terminah ${\tilde h}_{\mu\nu}$ s pomosh'yu spravedlivogo v lineinom priblizhenii sootnosheniya


		$\displaystyle \hat l^{\mu\nu}=a^2\sqrt{-\bar g}(-\bar g^{\mu\rho}\bar g^{\nu\si... ...}+{{\textstyle{\frac{1}{2}}}}e^{\mu\nu}e^{\rho\sigma}) {\tilde h}_{\rho\sigma}.$

Opredelim 3-tenzory:

$\begin{displaymath} q^m_l = {\tilde h}^m_l-\delta^m_l{\tilde h}^n_n, Q^m_l =... ..._{0n})\delta^m_l+\nabla^m {\tilde h}_{0l}- \partial_0 {q^m_l}. \end{displaymath}$

(3.19)

Krome togo, simvolom $\cal Q$ oboznachim vozmushennyi sled vneshnei krivizny giperpoverhnosti $\eta=const$ . Esli $n^\mu$ yavlyaetsya edinichnym vektorom normali k etoi giperpoverhnosti, to

$\begin{displaymath} {\cal Q}\equiv-D_\mu n^\mu-(-\overline{D_\mu n^\mu}) = {\tex... ...}{2}}}}\partial_0 {{\tilde h}}^{n}_n- \nabla_n {\tilde h}_0^n. \end{displaymath}$

(3.20)

Togda dlya konformnyh killingovyh vektorov, udovletvoryayushih (3.8), raschet po formule (24) lekcii 2: $\hat {\cal I}^{\mu} = \hat {\cal T}^\mu_\nu\xi^\nu + \hat {\cal Z}^\mu$ s

$\hat {\cal T}^{\mu\nu} = (\hat T^{(\mu}_\rho\overline g^{\nu)\rho} -\overline {... ...rline g^{\mu\nu} + {1\over \kappa} {\hat l}^{\lambda[\mu} \bar R^{\nu]}_\lambda$

$2\kappa \hat {\cal Z}^\mu = 2\left(\bar z^{\rho\sigma}\overline D_\rho \hat l^... ...l^{\mu\nu}\overline D_\nu \bar z - \bar z\overline D_\nu \hat l^{\mu\nu}\right)$ ,

(gde $\bar z_{\rho\sigma} = \overline D_{(\rho} \xi_{\sigma)}$ ), i s ispol'zovaniem oboznacheniya (3.20) daet:

$\begin{displaymath} \kappa\hat{\cal I}^0 = \kappa a^4\sqrt{f}\delta T^0_\mu \xi^... ...n_n+\nabla_n(\textstyle{1\over 4}\bar z{\tilde h}^n_0)\right], \end{displaymath}$

(3.21)

gde $\textstyle{1\over 4}\bar z=\dot a \xi^0+{\textstyle{1\over 3}}\nabla_k\xi^k$ , $\bar y= \nabla^2 {\xi^0}+3k \xi^0$ i $\nabla^2=f^{kl}\nabla_k\nabla_l$ .

Raschet po formule (26) lekcii 2:


		$\displaystyle \hat {\cal I}^{\mu\nu} ={1 \over \kappa} \hat l^{\rho[\mu}\overline D_\rho\xi^{\nu]} + \hat {\cal P}^{\mu\nu}{_\lambda} \xi^\lambda,$

gde


		$\displaystyle \hat {\cal P}^{\mu\nu\rho} = {1 \over 2\kappa} \overline D_\sigma... ...\bar g^{\sigma\mu} \hat l^{\nu\rho}+\bar g^{\sigma\nu} \hat l^{\mu\rho}\right),$

i s ispol'zovaniem oboznachenii (3.19), daet:

$\begin{displaymath} \kappa\hat{\cal I}^{0l}= {\textstyle{1 \over 2}} a^2 \sqrt{f... ...{\xi^0}+Q^l_k\xi^k+ {\tilde h}_{0k}\nabla^{[k}\xi^{l]}\right]. \end{displaymath}$

(3.22)

3.3.2 Integral'nye velichiny i ih svyazi

Teper' my imeem vse neobhodimoe, chtoby prointegrirovat' uravnenie (3.16) po sfericheskomu ob'emu V s granicei S v fiksirovannoe vremya $\eta$ . Opredelim

$\begin{displaymath} F({\bf\xi}) \equiv \int_V \hat {\cal I}^0 d^3x = \oint_S \hat {\cal I}^{0l}{\textstyle{\frac{1}{2}}}\epsilon_{lmn}dx^mdx^n. \end{displaymath}$

(3.23)

Esli etot integral (proshe analizirovat' poverhnostnyi integral, kotoryi zavisit tol'ko ot vozmushenii metriki) ne zavisit ot $\eta$ , to F yavlyaetsya integralom dvizheniya. Fakticheski my imeem 15 velichin F, po odnomu na kazhdyi konformnyi vektor Killinga ${\bf\xi}_A (A=1,2,...,15)$ . Mozhno sostavit' lineinye kombinacii iz F s vremenizavisimymi koefficientami, skazhem $c^A(\eta)F(\xi_A)$ . Poskol'ku vyrazheniya i (3.21), i (3.22) lineino zavisyat ot $\xi^\mu$ i tol'ko ih prostranstvennyh proizvodnyh, to $c^AF(\xi_A)=F(c^A\xi_A)$ . Voobshe govorya, $c^A\xi_A$ c $c^A = c^A(\eta)$ uzhe ne yavlyayutsya konformnymi vektorami Killinga, no kak my seichas uvidim nekotorye takie kombinacii okazyvayutsya kraine prostymi i imeyut fizicheskuyu interpretaciyu v podhodyashei kallibrovke. Davaite predstavim eti udobnye kombinacii.

Sem' iz opredelennyh vyshe konformnyh killingovyh vektorov my ostavlyaem bez izmeneniya, ih komponenty opredelyayutsya kak

$\begin{displaymath} {\bf t} =(1,0), {\bf s}_a =(0, \delta^k_a r'), {\bf r}_a = (0, \epsilon_{kal}x^l), \end{displaymath}$

(3.24)

gde $r=\sin \chi, \chi$ ili $\sinh \chi$ v zavisimosti ot k=1, 0 ili -1; i r' -- proizvodnaya po $\chi$ . Sleduyushie 8 lineinyh kombinacii, oboznachennye vektorami s krestami, sostavleny s pomosh'yu vremenizavisimyh koefficientov. V etih formulah ispol'zuyutsya oboznacheniya $\alpha = \sin \eta$ dlya k = 1 (ili $\sinh \eta$ dlya k= -1); gde $\alpha'$ est' proizvodnaya $\alpha$ po $\eta$ . Sleduyushie 4 vektora ne imeyut prostranstvennyh komponent:

$\displaystyle {\bf l}^\dagger_a$	=	$\displaystyle \left.\left( \alpha'{\bf l}_a- \alpha {\bf b}_a\right)\right\vert... ...1} = \left.\left({\bf l}_a - \eta {\bf s}_a\right)\right\vert _{k=0}= (x^a, 0),$
$\displaystyle \left.{\bf a}^\dagger\right\vert _{k=\pm 1}$	=	$\displaystyle \left.\left( \alpha'{\bf a}+ k\alpha{\bf d}\right)\right\vert _{k = \pm 1}= (r',0),$
$\displaystyle \left.{\bf a}^\dagger\right\vert _{k=0}$	=	$\displaystyle \left.\left({\textstyle{\frac{1}{2}}} {\bf a}- \eta{\bf d}+{\text... ...{2}}} \eta^2{\bf t}\right)\right\vert _{k=0}=({\textstyle{\frac{1}{2}}} r^2,0).$	(3.25)

Ostavshiesya 4 kombinacii ne imeyut vremennyh komponent i predstavlyayut konformnye killingovy vektory na secheniyah: $\eta={\rm const}$ :

$\displaystyle {\bf d}^\dagger$	=	$\displaystyle \left.\left(\alpha'{\bf d} - \alpha{\bf a}\right)\right\vert _{k=\pm 1}= \left.\left({\bf d}-\eta{\bf t}\right)\right\vert _{k=0}=(0,x^k r'),$
$\displaystyle \left.{\bf b}^\dagger_{a}\right\vert _{k=\pm 1}$	=	$\displaystyle \left.\left( \alpha' {\bf b}_a+ k\alpha{\bf l}_a\right)\right\vert _{k = \pm1}= (0, f^{ak}),$
$\displaystyle \left.{\bf b}^\dagger_{a}\right\vert _{k=0}$	=	$\displaystyle \left.\left(-{\textstyle{\frac{1}{2}}}{\bf b}_a+\eta{\bf l}_a- {\... ...ight)\right\vert _{k=0} =(0, \delta^{ak} {\textstyle{\frac{1}{2}}} r^2-x^ax^k).$	(3.26)

Kak vidno, kombinacii podobrany tak, chto vse komponenty vseh vektorov ne zavisyat ot vremeni.

Podstavlyaya v (3.21) i (3.22) vektory s komponentami (3.24), (3.25) i (3.26), poluchim integral'nye sootnosheniya (3.23), sootvetstvuyushie kazhdoi gruppe vektorov (3.24) - (3.26). V kachestve elementov integrirovaniya sleduet schitat' $dV=a^3\sqrt{f}d^3x$ i $dS_l= a^2\sqrt{f}{\textstyle{\frac{1}{2}}} \epsilon_{lmn}dx^m dx^n$ , ispol'zuetsya takzhe obychnoe opredelenie postoyannoi Habbla: $H=\dot a/a$ . Takim obrazom dlya vektorov (3.24) imeem

$\displaystyle \kappa F({\bf t})$	-	$\displaystyle aH\oint_S{\tilde h}_0^l dS_l = \int_V [(a\kappa\delta T^0_0+2H{\c... ...over a}{\tilde h}^m_m]dV =-{\textstyle{\frac{1}{2}}}\oint_S \nabla_kq^{kl}dS_l,$
$\displaystyle \kappa F({\bf s}_a)$	=	$\displaystyle \int_V a\kappa\delta T^0_a r'dV =\oint_S ({\textstyle{\frac{1}{2}}} Q^l{_k}s^k_a- k{\tilde h}_{0k}x^{[k}s_a^{l]})dS_l,$
$\displaystyle \kappa F({\bf r}_a)$	=	$\displaystyle \int_V a\kappa\delta T^0_k\epsilon_{kal}x^ldV =\oint_S ({\textsty... ...k}x^{[k}r_a^{l]}+ {\textstyle{\frac{1}{2}}} {\tilde h}_{0k}\epsilon_{kal})dS_l.$	(3.27)

Sootvetstvenno dlya (3.25):

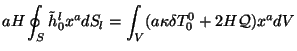
$\displaystyle \kappa F({\bf l}^\dagger_a)$	-	$\displaystyle aH \oint_S {\tilde h}_0^l x^a dS_l = \int_V (a\kappa\delta T^0_0+2H{\cal Q})x^adV$
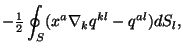
	=	$\displaystyle - {\textstyle{\frac{1}{2}}}\oint_S (x^a\nabla_k q^{kl}-q^{al})dS_l,$
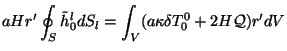
$\displaystyle \left.\kappa F({\bf a}^\dagger)\right\vert _{k=\pm 1}$	-	$\displaystyle aHr'\oint_S{\tilde h}_0^l dS_l = \int_V (a\kappa \delta T^0_0+2H {\cal Q})r'dV$
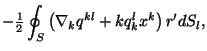
	=	$\displaystyle - {\textstyle{\frac{1}{2}}} \oint_S \left( \nabla_k q^{kl} + k q^l_kx^k\right) r'dS_l,$
$\displaystyle \left.\kappa F({\bf a}^\dagger)\right\vert _{k=0}$	-	$\displaystyle {\textstyle{\frac{1}{2}}} aH\oint_S {\tilde h}_0^lr^2 dS_l = \int... ...le{\frac{1}{2}}} a\kappa \delta T^0_0+H{\cal Q})r^2-{1\over a}{\tilde h}^m_m]dV$
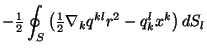
	=	$\displaystyle -{\textstyle{\frac{1}{2}}} \oint_S \left( {\textstyle{\frac{1}{2}}} \nabla_k q^{kl} r^2 - q^l_k x^k\right)dS_l$	(3.28)

i dlya (3.26):

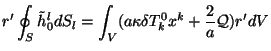
$\displaystyle \kappa F({\bf d}^\dagger)$	-	$\displaystyle r'\oint_S{\tilde h}_0^l dS_l = \int_V (a\kappa \delta T^0_k x^k+{2\over a}{\cal Q}) r'dV$
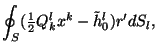
	=	$\displaystyle \oint_S ({\textstyle{\frac{1}{2}}} Q^l_k x^k-{\tilde h}^l_0)r'dS_l,$
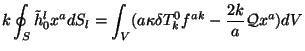
$\displaystyle \left.\kappa F({\bf b}^\dagger_a)\right\vert _{k=\pm 1}$	+	$\displaystyle k\oint_S {\tilde h}_0^l x^a dS_l = \int_V (a\kappa \delta T^0_kf^{ak}-{2k\over a}{\cal Q}x^a)dV$
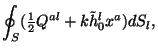
	=	$\displaystyle \oint_S ({\textstyle{\frac{1}{2}}} Q^{al}+k{\tilde h}^l_0 x^a)dS_l,$
$\displaystyle \left.\kappa F({\bf b}^\dagger_a)\right\vert _{k=0}$	+	$\displaystyle \oint_S {\tilde h}_0^l x^a dS_l = \int_V [a\kappa \delta T^0_k(\delta^{ak}{\textstyle{\frac{1}{2}}} r^2-x^ax^k)-{2\over a}{\cal Q}x^a]dV$
	=	$\displaystyle \oint_S [{\textstyle{\frac{1}{2}}} kQ^l_k(\delta^{ak}{\textstyle{... ...}{2}}} r^2-x^ax^k)+{\tilde h}^l_0 x^a +{\tilde h}_{0k}x^{[k}\delta^{l]}_a]dS_l.$	(3.29)

Integral'nye velichiny dlya nastoyashih konformnyh killingovyh vektorov fridmanovskoi geometrii legko vosstanavlivayutsya iz (3.28) i (3.29) s pomosh'yu obratnyh lineinyh kombinacii s vremenizavisimymi koefficientami.

<< 3.2 Konformnye vektory Killinga dlya ... | Oglavlenie | 3.4 Novye integral'nye sootnosheniya >>

Publikacii s klyuchevymi slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Sm. takzhe: Padenie shara v Solnechnoi sisteme Gravitacionnye anomalii na Merkurii Galaktika Arp 94 Sputniki GRAIL sostavlyayut kartu lunnoi gravitacii 70 let Stivenu Hokingu Molotok protiv peryshka na Lune Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce