Astronet > 3.4 Ispol'zovanie i interpretaciya novyh integral'nyh sootnoshenii

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 3.3 Zakony sohraneniya i ... | Oglavlenie | Literatura k Lekcii 3 >>

Razdely

3.4 Ispol'zovanie i interpretaciya novyh integral'nyh sootnoshenii

3.4.1 Svyazevye integral'nye vektory Trashen i effekt Saksa-Vol'fa

Na kachestvennom urovne my predstavlyaem rezul'tat [2], gde pokazano, chto esli na vozmusheniya material'noi sostavlyayushei na kosmologicheskom fone nalozheny ogranicheniya, to est' oni udovletvoryayut tak nazyvaemym integral'nym svyazyam, effekt Saksa-Vol'fa mozhet byt' oslablen. Dlya etogo nuzhno predstavlyat', chto takoe lokalizovannye vozmusheniya. Snachala opredelim ih v ploskom prostranstve-vremeni. Pust' v nachal'nyi moment vremeni t = 0 plotnost' $\rho$ yavlyaetsya odnorodnoi. V sleduyushii moment t > 0 v ob'eme V voznikayut vozmusheniya $\delta\rho$ , kotoryh net na granice ob'ema $\partial\Sigma$ . Eti vozmusheniya nazyvayutsya lokalizovannymi, esli oni udovletvoryayut integral'nym sootnosheniyam

$\begin{displaymath} \int_\Sigma \delta\rho dV =0, \int_\Sigma \vec x \delta\rho dV =0, \end{displaymath}$

(3.30)

kotorye nazyvayutsya integral'nymi svyazyami.

V OTO integral'nye svyazi imeyut vid:

$\begin{displaymath} \int_\Sigma \delta T^\alpha_\mu V^\mu n_\alpha dV = \oint_{\partial\Sigma} B^l d S_l. \end{displaymath}$

(3.31)

Ih smysl v tom, chto zadavaya granichnye usloviya my ogranichivaem vozmusheniya vnutri ob'ema. Analogichno (3.30), lokalizovannye vozmusheniya v OTO opredelyayutsya kak

$\begin{displaymath} \int_\Sigma \delta T^\alpha_\mu V^\mu n_\alpha dV = 0. \end{displaymath}$

(3.32)

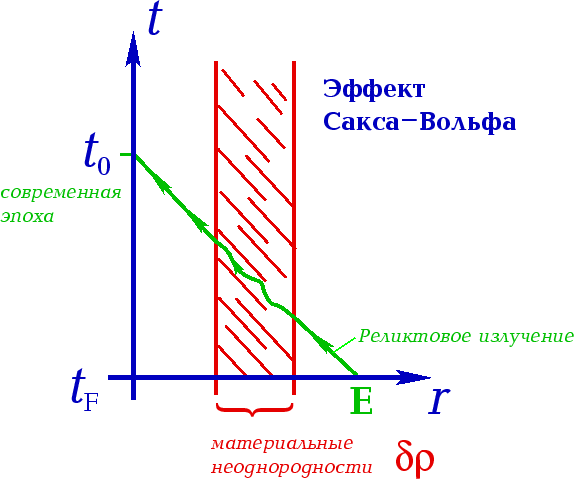
Dlya fridmanovskoi modeli sushestvuet 10 takih vektorov $V^\alpha$ , 6 iz nih -- eto uzhe izvestnye killingovy vektory fridmanovskogo fona. Ostavshiesya 4 vektora -- eto kak raz vektory Trashen [1].

Ris.2.

Effekt Saksa-Vol'fa [3] zaklyuchaetsya v tom, chto neodnorodnosti $\delta\rho$ na puti fonovogo kosmologicheskogo izlucheniya (Ris. 2) vnosyat vklad v anizotropiyu fonovoi temperatury. Sushestvovanie integral'nyh svyazevyh vektorov Trashen vedet k sushestvovaniyu lokalizovannyh vozmushenii tipa (3.32), kotorye oslablyayut etot effekt [2].

Teper' obratimsya k ob'emnym integralam v (3.27) - (3.29). Krome $\delta T^0_\mu$ podintegral'nye vyrazheniya v ob'emnyh integralah soderzhat lish' ${\cal Q}$ i ${\tilde h}^m_m$ . Sushestvuyut 4 lineinyh kombinacii F, kotorye ne vklyuchayut ${\tilde h}^m_m$ ; oni svyazany so sleduyushimi lineinymi kombinaciyami konformnyh killingovyh vektorov:

$\begin{displaymath} {\bf V}_0\equiv \left.(\dot a^{-1}{\bf a}^{\dag }-{\bf d}^{\... ...bf V}_a\equiv\dot a^{-1}{\bf l}^{\dag }_a+ k{\bf b}^{\dag }_a. \end{displaymath}$

(3.33)

Vektora ${\bf V}_0$ and ${\bf V}_a$ okazyvayutsya kak raz vektorami Trashen, a v kalibrovke ${\cal Q}=0$ sootvetstvuyushie integral'nye sootnosheniya s F obrashayutsya v integral'nye svyazi Trashen.

3.4.2 Kalibrovochnye usloviya i integral'nye sootnosheniya

V sootnosheniyah (3.27) - (3.29) ne byli fiksirovany kalibrovochnye usloviya, to est' svoboda vybora v otobrazhenii vozmushennogo prostranstva-vremeni na fonovoe ne byla ispol'zovana. Odno iz uslovii, kotoroe uproshaet pochti vse podintegral'nye vyrazheniya est' tak nazyvaemaya kalibrovka ,,odnorodnogo habblovskogo rasshireniya'' ${\cal Q}=0$ aktivno obsuzhdaemaya Bardinom [13]. Pri etom 14 iz 15 ob'emnyh podintegral'nyh vyrazhenii reduciruyutsya v kombinacii tol'ko $\delta T^0_\mu$ . Takim obrazom, eti 14 sootnoshenii vpolne priobretayut formu (3.31) i predstavlyayut novyi nabor integral'nyh svyazei. Ob'emnye integraly v etih integral'nyh svyazyah predstavlyayut momenty material'nogo tenzora energii-impul'sa poryadkov 0, 1 i 2 po x^a, kogda k=0, i blizkuyu interpretaciyu kogda $k=\pm 1$ . Ostavshiisya integral soderzhit kak $\delta T^0_\mu$ , tak i ${\tilde h}^m_m$ : dlya $k=\pm 1$ on otnositsya k konformnym vremennym translyaciyam $F({\bf t})$ , a dlya k=0 k vremennym uskoreniyam $F({\bf a}^{\dag })$ .

Chasto ispol'zuetsya drugoe kalibrovochnoe uslovie $\nabla_l \vtop{{\hbox{${\tilde h}^l_k$}} \vskip-5pt {\hbox{$\scriptscriptstyle T$}}}=0$ (sm., naprimer, rabotu [14]), v kotorom $\vtop{{\hbox{${\tilde h}^l_k$}} \vskip-5pt {\hbox{$\scriptscriptstyle T$}}}$ -- bessledovaya chast' ${\tilde h}^l_k$ . Kombiniruya $\nabla_l \vtop{{\hbox{${\tilde h}^l_k$}} \vskip-5pt {\hbox{$\scriptscriptstyle T$}}}=0$ s ${\cal Q}=0$ (eti 4 usloviya ispol'zovalis' Bichakom v neopublikovannoi rabote) my nahodim, chto sushestvuyut 4 sootnosheniya, kotorye ne zavisyat ot gravitacinnogo izlucheniya:


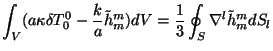		$\displaystyle \int_V (a\kappa \delta T^0_0-{k\over a}{\tilde h}^m_m)dV= {1\over 3}\oint_S \nabla^l{\tilde h}^m_m dS_l$


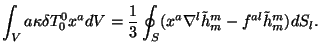		$\displaystyle \int_V a\kappa\delta T^0_0x^adV= {1\over 3}\oint_S (x^a\nabla^l{\tilde h}^m_m-f^{al}{\tilde h}^m_m) dS_l.$

Takim obrazom, v etoi kalibrovke integraly energii $\int \delta T^0_0$ i centra mass

$\int\delta T^0_0x^a/\int \delta T^0_0$ opredelyayutsya lish' sledom ${\tilde h}^m_m$ .

<< 3.3 Zakony sohraneniya i ... | Oglavlenie | Literatura k Lekcii 3 >>

Publikacii s klyuchevymi slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Sm. takzhe: Padenie shara v Solnechnoi sisteme Gravitacionnye anomalii na Merkurii Galaktika Arp 94 Sputniki GRAIL sostavlyayut kartu lunnoi gravitacii 70 let Stivenu Hokingu Molotok protiv peryshka na Lune Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce