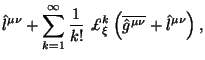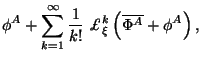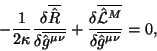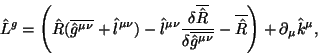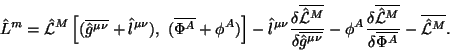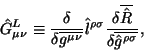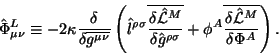Astronet > 4.2 Obobshennaya polevaya formulirovka OTO

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 4.1 Fiksirovannye fony v OTO | Oglavlenie | 4.3 Problemy polevoi formulirovki OTO >>

Razdely

4.2 Obobshennaya polevaya formulirovka OTO

4.2.1 Obobshenie modeli Dezera

V rabotah [13] $^{\!- }$ [16] my obobshili podhod predlozhennyi Dezerom [11]. Prezhde vsego, vmesto prostranstva Minkovskogo v lorencevyh koordinatah my predlagaem ispol'zovat' proizvol'no iskrivlennyi fon s zadannoi metrikoi $\bar g_{\mu\nu}$ i zadannymi fonovymi material'nymi polyami $\overline \Phi^A$ , udovletvoryayushimi fonovym uravneniyam Einshteina:

$\begin{displaymath} \overline G_{\mu\nu} = \kappa \overline T_{\mu\nu}. \end{displaymath}$

(4.8)

Chasto byvaet poleznym lish' Richchi-ploskii fon: $\overline G_{\mu\nu} = 0$ . Estestvenno, nasha polevaya formulirovka s fonom (4.8) yavlyaetsya kovariantnoi.

Kak okazalos', ispol'zovanie formalizma 1-go poryadka vovse ne obyazatel'no dlya postroeniya polnoi i zamknutoi (bez beskonechnyh razlozhenii) teorii. Teriya mozhet byt' postroena tak, chto nekotorye funkcii ne budut imet' yavnogo vyrazheniya cherez dinamicheskie peremennye, no uravneniya, kotorym oni udovletvoryayut dostatochno prosty i issledovanie ne vyzyvaet trudnostei. Chasto takoi formalizm 2-go poryadka bolee udoben i zdes' my ispol'zuem imenno ego dlya predstavleniya rezul'tatov.

Poka zapishem deistvie, kotoroe obobshaet deistvie Dezera bez konkretnogo vida lagranzhianov (ih my opredelim pozzhe) dlya gravitacionnogo polya $\hat l^{\mu\nu}$ i nabora material'nyh polei $\phi^A$ :

$\begin{displaymath} S = - {1 \over 2 \kappa c} \int{d^4x\hat L^g} + {1 \over c}\int{d^4x\hat L^m}. \end{displaymath}$

(4.9)

My polagaem, chto polya $\phi^A$ yavlyayutsya proizvol'nymi tenzornymi plotnostyami. Var'irovanie (4.9) po gravitacionnym peremennym $\hat l^{\mu\nu}$ daet uravnenie

$\begin{displaymath} \hat G^L_{\mu\nu}(l) + \hat \Phi^L_{\mu\nu}(l) = \kappa \lef... ...+ \hat t^{m}_{\mu\nu}\right) = \kappa \hat t^{(tot)}_{\mu\nu}, \end{displaymath}$

(4.10)

gde kovariantizovannyi operator bezmassovogo polya spina 2, obobshayushii operator v (4.1), est'

$\begin{displaymath} 2\hat G^L_{\mu\nu}(l) \equiv \overline D^\alpha_{ \alpha} \h... ...l^\alpha_{ \mu} - \overline D_{\alpha\mu}\hat l^\alpha_{ \nu}. \end{displaymath}$

(4.11)

Operator $\hat \Phi^L_{\mu\nu}(l,\phi)$ opredelim pozzhe, no zametim, chto dlya Richchi-ploskogo fona $\overline R_{\mu\nu} = 0$ on ischezaet i (4.10) preobrazuetsya v

$\begin{displaymath} \hat G^L_{\mu\nu}(l) = \kappa \left( \hat t^{gr}_{\mu\nu} + \hat t^{m}_{\mu\nu}\right) = \kappa \hat t^{(tot)}_{\mu\nu}. \end{displaymath}$

(4.12)

Pravaya chast' v uravneniyah (4.10) i (4.12) yavlyaetsya simmetrichnym (metrichesmkim) tenzorom energii-impul'sa sistemy, sootvetstvuyushim deistviyu (4.9):

$\begin{displaymath} \hat t^{gr}_{\mu\nu} = -{1\over{\kappa}} {{\delta{\hat L^g}}... ..._{\mu\nu} = 2{{\delta{\hat L^m}}\over{\delta\bar g^{\mu\nu}}}. \end{displaymath}$

(4.13)

Okazyvaetsya, chto dlya Richchi-ploskogo fona divergenciya ot levoi chasti uravnenii (4.12) obrashaetsya tozhdestvenno v nul':

$\begin{displaymath} \overline D_\nu \hat G^{L\nu}_{\mu}(l) \equiv 0, \end{displaymath}$

(4.14)

a eto vedet k zakonu sohraneniya

$\begin{displaymath} \overline D_\nu \hat t^{(tot)\nu}_{\mu} = 0. \end{displaymath}$

(4.15)

Takoi zakon ne vypolnyaetsya dlya obshego fona v uravneniyah (4.10) i eta problema budet obsuzhdat'sya pozzhe.

Analogichno tomu kak postroeny gravitacionnye uravneniya (4.10) stroyatsya material'nye uravneniya, gde levaya chast' lineina po dinamicheskim peremennym, a pravaya predstavlyaet nekotoryi ,,tok''.

Ekvivalentnost' OTO ustanavlivaetsya posle otozhdestvlenii

$\begin{displaymath} \sqrt{-g}g^{\mu\nu} \equiv \hat g^{\mu\nu} \equiv \overline ... ...\nu}} +\hat l^{\mu\nu}, \Phi^A = \overline \Phi^A + \phi^A, \end{displaymath}$

(4.16)

kotorye obobshayut (4.5) ili (4.7).

V sravnenii s rabotoi Dezera nami [13] $^{\!- }$ [16] byla podrobno ,,oboznachena'' i issledovana kalibrovochnaya (tak nazyvaemaya vnutrennyaya) invariantnost'. To est' invariantnost' otnositel'no preobrazovanii, kotorye ne zatragivayut ni koordinat, ni fonovoi metriki s fonovymi polyami. Eti preobrazovaniya vyglyadyat tak

$\displaystyle {\hat l}'^{\mu\nu}$	=	$\displaystyle \hat l^{\mu\nu} + \sum^{\infty}_{k = 1}{1\over{k!}} \hbox{$\pounds$}_\xi^k \left(\overline {\hat g^{\mu\nu}} + \hat l^{\mu\nu}\right),$
$\displaystyle {\phi}'^A$	=	$\displaystyle \phi^A + \sum^\infty_{k = 1}{1\over{k!}} \hbox{$\pounds$}_\xi^k \left(\overline{\Phi^A}+\phi^A\right),$	(4.17)

gde, voobshe govorya, ne predpolagaetsya ni malosti polei, ni malosti kalibrovochnyh funkcii (konechno, bez predpolozhenii o malosti neobhodimo uchityvat' vse poryadki v beskonechnyh ryadah). Invariantnost' sostoit v sleduyushem. Lagranzhian v (4.1) invarianten dlya preobrazovanii (4.17) s tochnost'yu do divergencii na fonovyh uravneniyah dvizheniya. Takim obrazom, samo deistvie (4.1) invariantno s tochnost'yu do poverhnostnyh chlenov. Uravneniya dvizheniya yavlyayutsya kalibrovochno invariantnymi na nih samih (to est', esli oni udovletvoreny) i na fonovyh uravneniyah. Tenzor energii-impul'sa kalibrovchno invarianten, no s tochnost'yu do divergencii:

$\begin{displaymath} {\hat t}'^{(tot)}_{\mu\nu} = {\hat t}^{(tot)}_{\mu\nu} + {1 \over \kappa} \hat G^L_{\mu\nu}\left(l' - l\right), \end{displaymath}$

(4.18)

gde operator $\hat G^L_{\mu\nu}\left(l' - l\right)$ opredelen v (4.11) i yavlyaetsya 4-kovariantnoi divergenciei. Podrobnee svoistva i nekotorye prilozheniya kalibrovochnyh preobrazovanii v polevom podhode budut dany v sleduyushei lekcii 5.

4.2.2 Principy postroeniya oboshennoi polevoi formulirovki OTO

Razvivaya polevuyu formulirovku OTO (sm. uravneniya (4.8) - (4.18)), dlya postroeniya my [13] ispol'zovali princip predlozhennyi Dezerom:

I.Istochnikom lineinogo bezmassovogo polya spina 2 v gravitacionnyh uravneniyah dolzhen byt' simmetrichnyi tenzor energii-impul'sa vseh dinamicheskih polei, vklyuchaya gravitacionnoe pole.

Takim obrazom stroyatsya uravneniya (4.12). V bolee slozhnom sluchae uravnenii (4.10) princip postroeniya istochnika v pravoi chasti sohranyaetsya, uslozhnyaetsya lish' opredelenie levoi lineinoi chasti.

Drugoi princip, ispol'zuetsya v rabote Grishuka [17] i mozhet byt' sformulirovan kak

II.Ot gravistatiki (ot zakona N'yutona) k gravidinamike (k uravneiyam Einshteina).

Sposob postroeniya po etomu principu zaklyuchaetsya v obobshenii zakona Nyutona $\Delta \phi = 4\pi G\rho$ na sluchai special'noi teorii otnositel'nosti:

(i) Snachala odna komponenta plotnosti $\rho$ zamenyaetsya na 10 komponent material'nogo tenzora energii-impul'sa $T_{\mu\nu}$ .

(ii) Iz etogo sleduet, chto odnu komponentu gravitacionnogo potenciala $\phi$ nuzhno zamenit' 10-yu gravitacionnymi potencialami $h^{\mu\nu}$ .

(iii) Dalee neobhodimo laplasian $\Delta$ zamenit' na dalambertian, kak eto dolzhno byt' v special'noi teorii otnositel'nosti: $h_{\mu\nu ,\alpha}^{ ,\alpha} = \kappa T_{\mu\nu}$ .

(iv) Sleduyushii shag -- eto vklyuchenie samodeistviya:

$h_{\mu\nu ,\alpha}^{ ,\alpha} = \kappa\left(T_{\mu\nu} + t^{gr}_{\mu\nu}\right) = \kappa t^{(tot)}_{\mu\nu}$ .

(v) I, nakonec, dobavlenie k levoi chasti chlenov

$\eta_{\mu\nu}h^{\alpha\beta}_{ ,\alpha\beta}- h^{\alpha}_{ \mu,\nu\alpha} - h^{\alpha}_{ \nu,\mu\alpha}$ vostanavlivaet kalibrovochnuyu invariantnost' teorii.

V rezul'tate poluchayutsya uravneniya $G^L_{\mu\nu}(h) = \kappa t^{(tot)}_{\mu\nu}$ , kotorye est' uravneniya (4.12) i est' tochno uravneniya Einshteina.

Tretii princip osnovyvaetsya na kalibrovochno invariantnyh svoistvah polevoi formulirovki [16] i blizok k tomu kak mogut byt' postroeny mnogie iz kalibrovochnyh teorii. Etot princip postroeniya zaklyuchaetsya v lokalizacii parametrov nekotoroi gruppy preobrazovanii, otnositel'no kotoroi ishodnaya teoriya invariantna. Lokalizaciya zaklyuchaetsya v tom, chto postoyannye parametry stanovyatsya zavisimymi, skazhem, ot koordinat. Voznikshaya neinvariantnost' kompensiruetsya kak raz vnov' vvedennymi kallibrovochnymi (kompensiruyushimi) polyami. Nash princip zvuchit kak

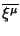III. ,,Lokalizaciya'' fonovyh vektorov Killinga $\overline {\xi^\mu}$ ,

i svoditsya k sleduyushemu:

(i) Rassmotrim sistemu dinamicheskih polei $\phi^A$ na zadannom fone (s metrikoi $\bar g^{\mu\nu}$ i obladayushim vektorami Killinga $\overline {\xi^\mu}$ ) s lagranzhianom $L^M(\phi^A, \bar g^{\mu\nu})$ .

(ii) Otnositel'no ,,kalibrovochnyh'' preobrazovanii $\phi'^A \rightarrow \phi^A + \hbox{$\pounds$}_{\bar\xi}\phi^A$ , v lineinom priblizhenii po $\overline {\xi^\mu}$ , uravneniya sistemy invariantny na samih sebe, a lagranzhian invarianten s tochnost'yu do divergencii.

(iii) Teper' ,,lokalizuem'' kakoi libo iz vektorov $\overline {\xi^\mu}$ , zdes' pod lokalizaciei my ponimaem zamenu vektora Killinga na proizvol'nyi vektor $\xi^\mu$ .

(iv) Posle etogo trebuem sohraneniya prezhnei invariantnosti. Chtoby udovletvorit' etomu trebovaniyu neobhodimo vvesti kompensiruyushee (gravitacionnoe) pole $h^{\mu\nu}$ takim obrazom, chto $\bar g^{\mu\nu} \rightarrow \bar g^{\mu\nu} + h^{\mu\nu}$ . Posledovatel'noe postroenie teorii polei $h^{\mu\nu}$ privodit k obobshennoi polevoi formulirovke OTO.

4.2.3 Postroenie oboshennoi polevoi formulirovki OTO s pomosh'yu razdeleniya na fon i dinamicheskie polya

Chetvertyi princip postroeniya oboshennoi polevoi formulirovki my vydelyaem v otdel'nyi podpunkt, poskol'ku udelim emu bol'she vnimaniya. Imenno takoe postroenie daet bolee naglyadnuyu svyaz' mezhdu polevoi formulirovkoi i obychnoi geometricheskoi formulirovkoi OTO. Deistvitel'no, esli eto est' vsego lish' razlichnye predstavleniya odnoi i toi zhe teorii i perehod ot polei formulirovki k geometricheskoi dostigaetsya s pomosh'yu otozhdestvlenii (4.16), to veroyatno, chto perehod ot geometricheskoi formulirovki k polevoi mog by osushestvlyat'sya s pomosh'yu razbieniya tipa (4.16). Deistvitel'no, chasto po tem ili inym prichinam v OTO delayut razbienie einshteinovskoi metriki na fonovuyu i dinamicheskuyu chasti:

$\begin{displaymath} g_{\mu\nu} = \bar g_{\mu\nu} + h_{\mu\nu}. \end{displaymath}$

(4.19)

Zatem, podstavlyayut (4.19) v uravneniya Einshteina, ostavlyayut v levoi chasti lish' lineinye po vozmusheniyam chleny, a vse ostal'noe perenosyat vpravo i nazyvayut etot istochnik ,,effektivnym'' tenzorom energii-impul'sa:

$\begin{displaymath} G^L_{\mu\nu}(h) = \kappa t^{(eff)}_{\mu\nu}. \end{displaymath}$

(4.20)

V takom podhode net nichego protivorechivogo. Odnako samo postroenie yavlyaetsya evristicheskim i mnogie ego svoistva ne tak uzh prosto vyyasnit'. My [15] razvili podhod (4.19) - (4.20) kak polevuyu teoriyu so vsemi ee atributami. To est' predstavlen lagranzhian, iz kotorogo sleduyut uravneniya i tenzor energii-impul'sa, sleduyut kalibrovochnye svoistva. Zdes' my predstavlyaem osnovnye elementy etogo podhoda. Snachala sformuliruem sam princip postroeniya:

IV. Polevaya formulirovka OTO stroitsya s pomosh'yu razbienii peremennyh obychnoi geometricheskoi formulirovki OTO na fonovye i dinamicheskie chasti.

Rassmotrim obychnoe destvie OTO:

$\begin{displaymath} S = {1 \over c} \int d^4x {\hat{\cal L}}^{GR} \equiv -{1 \... ...+ {1 \over c} \int d^4x {\hat{\cal L}}^M (\Phi^A, g_{\mu\nu}). \end{displaymath}$

(4.21)

Sdelaem razlozhenie peremennyh na fonovye i dinamicheskie chasti,

$\begin{displaymath} \hat g^{\mu\nu} \equiv \overline {\hat g^{\mu\nu}} + \hat l^{\mu\nu}, \Phi^A \equiv \overline {\Phi^A} + \phi^A \end{displaymath}$

(4.22)

gde fonovye peremennye yavlyayutsya resheniyami fonovyh uravnenii Einshteina:

$\begin{displaymath} -{1 \over {2\kappa }} {{\delta \overline{\hat R}} \over {\d... ...t{\cal L}}^M}} \over {\delta \overline{\hat g^{\mu\nu}}}} = 0, \end{displaymath}$

(4.23)

$\begin{displaymath} {{\delta \overline{{\hat{\cal L}}^M}} \over {\delta \overline{\Phi^A}}} = 0. \end{displaymath}$

(4.24)

Razbieniya (4.22) tochno obratny otozhdestvleniyam (4.16) i obobshayut (4.19), a uravneniya (4.23) -- eto uravneniya (4.8). Postroenie dinamicheskogo lagranzhiana [15]:

$\begin{displaymath} {\hat{\cal L}}^{dyn} = {\hat{\cal L}}^{GR} - {\hat{\cal L}}^{(1)} - {\hat{\cal L}}^{(0)} + div, \end{displaymath}$

(4.25)

-- eto est' oboshenie konstrukcii Dezera [11]. Lagranzhian (4.25) -- eto lagranzhian v deistvii (4.9):


		$\displaystyle {\hat{\cal L}}^{dyn} = -{1\over{2\kappa}}\hat L^g + \hat L^m,$

gde ${\hat{\cal L}}^{(0)} \equiv \overline{{\hat{\cal L}}^{GR}}$ , ${\hat{\cal L}}^{(1)}$ proporcionalen uravneniyam (4.23) i (4.24), a $div = \partial_\mu \hat k^\mu$ c $\hat k^\mu \equiv \hat g^{\mu\rho} \Delta^\sigma_{\rho\sigma} - \hat g^{\rho\sigma} \Delta^\mu_{\rho\sigma}$ i $\Delta^\mu_{\rho\sigma} = \Gamma^\mu_{\rho\sigma}- \overline{ \Gamma^\mu_{\rho\sigma}}$ , takaya zhe kak v KBL modeli. Konkretno gravitacionnaya i material'nye chasti imeyut sleduyushee yavnoe vyrazhenie:

$\begin{displaymath} \hat L^g = \left(\hat R (\overline {\hat g^{\mu\nu}} + \hat ... ...\nu}}}} - \overline{\hat R}\right) + \partial_\mu \hat k^\mu, \end{displaymath}$

(4.26)

$\begin{displaymath} \hat L^m = {\hat{\cal L}}^M\left[(\overline {\hat g^{\mu\nu... ...over{\delta \overline{\Phi^A}}} - \overline{{\hat{\cal L}}^M}. \end{displaymath}$

(4.27)

Var'irovanie deistviya (4.9) so znacheniyami lagranzhianov (4.26) i (4.27) po gravitacionnym peremennym daet uravnenie (4.10):


		$\displaystyle \hat G^L_{\mu\nu} + \hat \Phi^L_{\mu\nu} = \kappa\left({\hat t}^g_{\mu\nu} + {\hat t}^m_{\mu\nu}\right) \equiv \kappa{\hat t}^{(tot)}_{\mu\nu},$

gde gravitacionnaya lineinaya chast' (4.11) mozhet byt' zapisana kak

$\begin{displaymath} \hat G^L_{\mu\nu} \equiv {\delta \over {\delta\overline{g^{... ...verline{\hat R}}\over{\delta \overline{\hat g^{\rho\sigma}}}}, \end{displaymath}$

(4.28)

a lineinaya material'naya chast' kak

$\begin{displaymath} \hat \Phi^L_{\mu\nu} \equiv -2\kappa {\delta \over {\delta\o... ...ine{{\delta {{\hat{\cal L}}^M}}\over{\delta {\Phi^A}}}\right). \end{displaymath}$

(4.29)

Polnyi tenzor energii-impul'sa sootvetstvuyushii (4.9) i po chastyam predstavlenyi v (4.13) est'

$\begin{displaymath} {\hat t}^{(tot)}_{\mu\nu} \equiv 2{{\delta{\hat{\cal L}}^{dy... ...^{\mu\nu}}}} \equiv {\hat t}^g_{\mu\nu} + {\hat t}^m_{\mu\nu}. \end{displaymath}$

(4.30)

V sleduyushei lekcii 5, ispol'zuya obshekovariantnye svoistva sistemy (4.21) i razbieniya (4.22), my pokazhem kak poluchit' vse kalibrovochnye svoistva polevoi formulirovki.

<< 4.1 Fiksirovannye fony v OTO | Oglavlenie | 4.3 Problemy polevoi formulirovki OTO >>

Publikacii s klyuchevymi slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Sm. takzhe: Padenie shara v Solnechnoi sisteme Gravitacionnye anomalii na Merkurii Galaktika Arp 94 Sputniki GRAIL sostavlyayut kartu lunnoi gravitacii 70 let Stivenu Hokingu Molotok protiv peryshka na Lune Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce