Astronet > 4.3 Problemy polevoi formulirovki OTO

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 4.2 Obobshennaya polevaya formulirovka OTO | Oglavlenie | 4.4 Metod Neter-Belinfante i ... >>

Razdely

4.3 Problemy polevoi formulirovki OTO

4.3.1 Differencial'nye zakony sohraneniya dlya obobshennoi formulirovki

Dlya gravitacionnyh uravnenii (4.10) polevoi formulirovki $\hat G^L_{\mu\nu} + \hat \Phi^L_{\mu\nu} = \kappa{\hat t}^{(tot)}_{\mu\nu}$ differencial'nyi zakon sohraneniya (4.15) vypolnyaetsya tol'ko dlya fonov, kotorye yavlyayutsya prostranstvami Einshteina po Petrovu [18]. Takim obrazom, dlya Richchi-ploskih fonov $\overline{R} = 0$ , v samom obshem sluchae dlya prostranstv Einshteina $\overline {R_{\mu\nu}} = \Lambda \bar g_{\mu\nu}$ vypolnyaetsya $\overline D_\nu \hat t^{(tot)\nu}_\mu = 0$ . Odnako, dlya bolee obshih fonov my ne imeem tozhdestva tipa (4.14), prihoditsya konstatirovat', chto $\overline D_\nu\left(\hat G^{L\nu}_{\mu} + \hat \Phi_{\mu}^{L\nu}\right) \neq 0$ i zaklyuchat', chto $\overline D_\nu \hat t^{(tot)\nu}_\mu \neq 0$ . Etot fakt my [13] ob'yasnili kak sledsvtie vzaimodeistviya so slozhnym fonom, no tol'ko na kachestvennom urovne. Takim obrazom, pervuyu problemu my formuliruem tak:

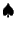$\spadesuit$ I? Mozhno li postroit' differencial'nye zakony sohraneniya na samom obshem fone? Kak oni vyglyadyat, kak vyglyadyat chleny vzaimodeistviya s fonom?

4.3.2 Proizvol'nye vektory smeshenii

Esli fon -- eto prostranstvo Einshteina (to est' vypolnyaetsya zakon (4.14)) i fon imeet killingovy vektory $\overline\xi^\alpha$ , togda neslozhno postroit' sohranyayushiisya tok

$\partial_\nu \left(\hat t^{(tot)\nu}_\mu \overline\xi^\mu\right)= 0$ i sootvetstvuyushie global'nye zakony sohraneniya. Odnako, kak otmechalos' v lekcii 3 vazhnymi mogut okazat'sya i ne tol'ko killingovy vektory. Ved' s pomosh'yu metoda Neter-Belinfante okazalos' vozmozhnym postroit' sohranyayushiesya toki dlya proizvol'nyh vektorov smeshenii. Poetomu vtoruyu problemu my sformuliruem sleduyushim obrazom:

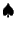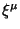$\spadesuit$ II? Mozhno li postroit' sohranyayushiesya toki dlya proizvol'nyh vektorov $\xi^\mu$ i kak oni budut vyglyadet'
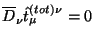(a) dlya sluchaya $\overline D_\nu \hat t^{(tot)\nu}_\mu = 0$ ?

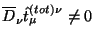(b) nesmotrya na to, chto $\overline D_\nu \hat t^{(tot)\nu}_\mu \neq 0$ ?

4.3.3 Superpotencialy v polevoi formulirovke OTO

Nachinaya s rabot Tolmena [19] i Freida [4.20] stalo yasno, chto superpotencialy v OTO igrayut vazhnuyu rol' v postroenii zakonov sohraneniya. Est' takzhe ukazaniya na to, chto oni imeyut mesto i v obobshennoi polevoi formulirovke OTO. Davaite rassmotrim uravneniya polevoi formulirovki na ploskom fone: $\hat G^{\mu\nu}_L = \kappa \hat t^{\mu\nu}_{(tot)}$ , gde levaya chast' opredelennaya v (4.11) mozhet byt' perepisana v vide $\hat G^{\mu\nu}_L = \overline D_\rho \hat {\cal P}^{\mu\nu\rho}$ s superpotencialom Papapetrou [21]: $\hat {\cal P}^{\mu\nu\rho}$ . Takim obrazom, v etom prostom sluchae obobshennyi tenzor energii-impul'sa vyrazhaetsya cherez divergenciyu ot superpotenciala. Abbott i Dezer [22] postroili obobshennyi superpotencial Papapetrou dlya sluchaya desitterovskogo i anti-desitterovskogo fona s vektorami Killinga etih zhe fonov. Tret'yu problemu my formuliruem poetomu v vide:

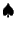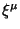$\spadesuit$ III? Kakovy superpotencialy v samoi obshei forme i s proizvol'nymi $\xi^\mu$ v obobshennoi polevoi formulirovke OTO?

4.3.4 Neopredelennost' Boul'vara-Dezera

Rassmatrivaya razlichnye razbieniya dlya opredeleniya vozmushenii na ploskom fone tipa $g_{\mu\nu} = \eta_{\mu\nu} + h_{\mu\nu}$ , $\sqrt {-g}g^{\mu\nu} = \eta^{\mu\nu} + \hat l^{\mu\nu},...$ Boul'var i Dezer [23] ustanovili, chto tenzory energii-impul'sa sootvetstvuyushie etim razbieniyam razlichayutsya, nachinaya so vtorogo poryadka po vozmusheniyam. My [15] issledovali etu problemu v samom obshem sluchae dlya proizvolnyh fonov. Dlya vseh vozmozhnyh razbienii tipa

$\displaystyle g_{\mu\nu}$	=	$\displaystyle \bar g_{\mu\nu} + h_{\mu\nu},$
$\displaystyle \hat g^{\mu\nu}$	=	$\displaystyle \overline {\hat g^{\mu\nu}} + \hat l^{\mu\nu}, ��\rightarrow g^A = \bar g^A + h^A$
$\displaystyle g^{\mu\nu}$	=	$\displaystyle \bar g^{\mu\nu} + r^{\mu\nu},$
....	=	............. ,	(4.31)

byl postroen svoi variant polevoi formulirovki s uravneniyami

$\begin{displaymath} \hat G^{L(A)}_{\mu\nu} + \hat \Phi^{L(A)}_{\mu\nu} = \kappa{\hat t}^{(tot�A)}_{\mu\nu}, \end{displaymath}$

(4.32)

gde gravitacionnye vozmusheniya vzyatye v forme $\hat l^{\mu\nu}_{(A)} \equiv h^A ({{ \partial \overline {\hat g^{\mu\nu}}} / {\partial \overline {g^A}}})$ obobshayut $\hat l^{\mu\nu}$ . V obshem sluchae byla naidena neopredelennost' v tenzore energii-impul'sa ${\hat t}^{(tot�A)}_{\mu\nu}$ v uravneniyah (4.32) dlya razlichnyh razbienii (4.31). Odnako, do sih por ne yasno kakoe iz razbienii (4.31) bolee predpochtitel'no. Chetvertaya problema poetomu est'

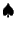$\spadesuit$ IV? Opredelenie kriteriya dlya vybora nailuchshih h^A.

<< 4.2 Obobshennaya polevaya formulirovka OTO | Oglavlenie | 4.4 Metod Neter-Belinfante i ... >>

Publikacii s klyuchevymi slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Sm. takzhe: Padenie shara v Solnechnoi sisteme Gravitacionnye anomalii na Merkurii Galaktika Arp 94 Sputniki GRAIL sostavlyayut kartu lunnoi gravitacii 70 let Stivenu Hokingu Molotok protiv peryshka na Lune Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce