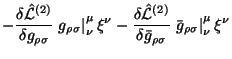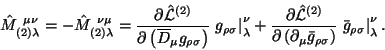- 4.4.1 Tozhdestvo Kaca-Bichaka-Linden-Bella
- 4.4.2 Tozhdestvo Neter dlya polevogo lagranzhiana
- 4.4.3 Superpotencial v polevoi formulirovke OTO
- 4.4.4 Sravnenie rezul'tatov metoda Neter-Belinfante i polevogo podhoda
- 4.4.5 Razreshenie neopredelennosti Boul'vara-Dezera
4.4 Metod Neter-Belinfante i polevoi podhod k OTO
Kombinaciya etih dvuh metodov pozvolyaet razreshit' opisannye v predydushei chasti problemy. Rezul'taty etoi chasti byli dolozheny na seminare [24].
4.4.1 Tozhdestvo Kaca-Bichaka-Linden-Bella
Napomnim kak byl poluchen zakon sohraneniya KBL [25].
Dlya lagranzhiana
kotoroe zatem preobrazovano v zakon sohraneniya (sm. (1.29) v lekcii 1):
Esli v processe preobrazovanii (4.34) ne ispol'zovat' uravnenii Einshteina i ne vezde yavno predstavlyat'
gde superpotencial kak i prezhde (sm. (31) v lekcii 1) imeet vid:
a tok v levoi chasti (4.36) imeet bolee obshii vid, chem v (4.35).
4.4.2 Tozhdestvo Neter dlya polevogo lagranzhiana
Gravitacionnyi lagranzhian v polevoi formulirovke (sm. (4.26))
est'
yavnaya forma kotorogo
Teper' ispol'zuem tozhdestvo Neter
![]() , chtoby preobrazovat' ego k vidu:
, chtoby preobrazovat' ego k vidu:
gde
Vychtem iz tozhdestva (4.36) tozhdestvo (4.41), uchtem ravenstvo
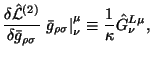 |
svyaz' (4.39), opredelenie (4.42) i poluchim novoe tozhdestvo:
predstavlennoe v terminah polevogo podhoda.
4.4.3 Superpotencial v polevoi formulirovke OTO
Eshe raz zapishem obshee uravnenie polevoi vormulirovki:
gde
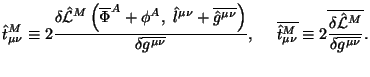 |
Teper', konechno, istochnik v (4.45) ne yavlyaetsya simmetrichnym tenzorom energii-impul'sa, sootvetstvuyushim dinamicheskomu lagranzhianu (4.25):
Obsudim eto uravnenie. Prezhde vsego, eto est' analog uravneniya KBL (4.35), zdes' v pravoi chasti takzhe stoit divergenciya teper' ot novogo superpotenciala
Pochemu etot uspeh ne byl dostignut ran'she?
Okazyvaetsya
bylo oshibochnym
predpolozhenie
(dlya postroeniya sohranyayushegosya toka
na proizvol'nom
fone) ispol'zovat' istochnik
![]() v pravoi chasti
(4.44),
opredelennyi standartnym
obrazom v (4.30). Okazyvaetsya neobhodimo ispol'zovat' vozmusheniya
v pravoi chasti
(4.44),
opredelennyi standartnym
obrazom v (4.30). Okazyvaetsya neobhodimo ispol'zovat' vozmusheniya
![]() . Otmet'te takzhe, chto v levoi chasti
(4.46)
soderzhitsya chlen vzaimodeistviya s fonom, prodeklarirovannyi kachestvenno
nami ran'she [13]. Z-chlen v (4.46),
kak i vezde, obrashaetsya v nul'
dlya vektorov Killinga fona.
. Otmet'te takzhe, chto v levoi chasti
(4.46)
soderzhitsya chlen vzaimodeistviya s fonom, prodeklarirovannyi kachestvenno
nami ran'she [13]. Z-chlen v (4.46),
kak i vezde, obrashaetsya v nul'
dlya vektorov Killinga fona.
4.4.4 Sravnenie rezul'tatov metoda Neter-Belinfante i polevogo podhoda
Glavnym rezul'tatom lekcii 2 bylo postroenie
zakona sohraneniya (sm. (24) v lekcii 2):
a superpotencial predstavlyaet soboi summu KBL superpotenciala i popravki Belinfante:
Perepishem uravnenie (4.46) v kompaktnom vide:
gde
Okazyvaetsya, chto popravka Belinfante, opredelennaya v (23) v lekcii 2
i spinovyi chlen (4.42)
sovpadayut:
![]() .
Uchityvaya etot fakt v (4.49) i v superpotenciale v
(4.51), zaklyuchaem
.
Uchityvaya etot fakt v (4.49) i v superpotenciale v
(4.51), zaklyuchaem
| = | |||
| = |
i
Takim obrazom vse svoistva
- Zakon sohraneniya (4.50) poluchen v ramkah polevogo podhoda i yavlyaetsya tochno uravneniem (4.47), kotoroe est' sledstvie metoda Neter-Belin- fante. Dva raznyh podhoda na urovne samyh obobshennyh zakonov sohraneniya dayut edinyi otvet.
Sravnivaya tenzory energii-impul'sa (4.48) i v (4.51)
nahodim, chto
tenzory
energii-impul'sa gravitacionnogo polya ne sovpadayut:
![]() .
(Tol'ko dlya sluchaya, kogda
.
(Tol'ko dlya sluchaya, kogda
![]() i
i ![]() my poluchaem, chto dolzhno byt'
my poluchaem, chto dolzhno byt'
![]() .)
Tem ne menee, s ispol'zovaniem fonovyh i dinamicheskih
uravnenii Einshteina ravenstvo (4.52) podtverzhdaetsya
pryamymi raschetami. Takaya situaciya govorit o slozhnosti v
opredelenii, naprimer, energii gravitacionnyh voln
na dostatochno slozhnyh fonah. Na etu problemu v chastnoi besede
ukazal Kopeikin [26].
.)
Tem ne menee, s ispol'zovaniem fonovyh i dinamicheskih
uravnenii Einshteina ravenstvo (4.52) podtverzhdaetsya
pryamymi raschetami. Takaya situaciya govorit o slozhnosti v
opredelenii, naprimer, energii gravitacionnyh voln
na dostatochno slozhnyh fonah. Na etu problemu v chastnoi besede
ukazal Kopeikin [26].
4.4.5 Razreshenie neopredelennosti Boul'vara-Dezera
Teper' rassmotrim poslednyuyu:
chetvertuyu problemu polevogo podhoda --
eto neopredelennost' v vybore razbienii (4.31).
Esli my vyberem proizvol'noe iz razbienii (4.31):
Raznica lish' v tom, chto argument v etom uravnenii zavisit ot vybora razbieniya (4.53) i vyrazhaetsya cherez nego kak
Napomnim, chto superpotencial
Vernemsya k metodu Neter-Belinfante:
ne bylo ogranichenii v vybore peremennyh, my mogli vybrat'
lyubuyu iz nih:
![]() !
V rezul'tate, konechnym i lineinym okazalsya edinstvenno KBL
superpotencial,
!
V rezul'tate, konechnym i lineinym okazalsya edinstvenno KBL
superpotencial,
![]() , a zatem novyi superpotencial,
, a zatem novyi superpotencial,
![]() . Tol'ko dlya vybora
(4.31), ili v
(4.55), edinstvenno
. Tol'ko dlya vybora
(4.31), ili v
(4.55), edinstvenno
![]() superpotencial
superpotencial
![]() v (4.54) i
v (4.54) i
![]() sovpadayut.
Etot fakt svidetel'stvuet o preimushestve vybora (4.22).
Sushestvuyut i drugie pokazaniya v pol'zu etogo
vybora i razbieniya, sootvetvuyushego emu.
Superpotencial Abbotta-Dezera [22]
yavlyaetsya odnim iz nabora (4.54), a imenno:
sovpadayut.
Etot fakt svidetel'stvuet o preimushestve vybora (4.22).
Sushestvuyut i drugie pokazaniya v pol'zu etogo
vybora i razbieniya, sootvetvuyushego emu.
Superpotencial Abbotta-Dezera [22]
yavlyaetsya odnim iz nabora (4.54), a imenno:
![]() .
Odnako my [27] pokazali,
chto takoi superpotencial ne daet pravil'nogo Bondi-Saksa impul'sa
na nulevoi beskonechnosti, to est' ne udovletvoryaet odnomu iz osnovnyh
estestvennyh testov,
v to vremya kak
.
Odnako my [27] pokazali,
chto takoi superpotencial ne daet pravil'nogo Bondi-Saksa impul'sa
na nulevoi beskonechnosti, to est' ne udovletvoryaet odnomu iz osnovnyh
estestvennyh testov,
v to vremya kak
![]() daet nuzhnyi rezul'tat.
daet nuzhnyi rezul'tat.
<< 4.3 Problemy polevoi formulirovki OTO | Oglavlenie | Literatura k Lekcii 4 >>
|
Publikacii s klyuchevymi slovami:
zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
![$\displaystyle \left[ {{\partial {\hat{\cal L}}_G} \over {\partial \left(\bar D_...
...
\overline D_\nu g_{\rho\sigma} - {\hat{\cal L}}_G \delta^\mu_\nu\right]\xi^\nu$](https://images.astronet.ru/pubd/2001/09/12/0001170672/img516.gif)
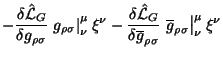
![$\displaystyle \left[{{\partial {\hat{\cal L}}^{(2)}} \over {\partial \left(\bar...
...erline D_\nu g_{\rho\sigma} - {\hat{\cal L}}^{(2)}\delta^\mu_\nu\right]
\xi^\nu$](https://images.astronet.ru/pubd/2001/09/12/0001170672/img527.gif)