Astronet > 5.1 Kalibrovochnye preobrazovaniya v polevoi formulirovke OTO

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 5. Interpretaciya i prilozheniya ... | Oglavlenie | 5.2 Izolirovannye sistemy na ... >>

Razdely

5.1 Kalibrovochnye preobrazovaniya v polevoi formulirovke OTO

Kalibrovochnye preobrazovaniya i ih svoistva v polevoi formulirovke pryamo vytekayut iz obshei kovariantnosti OTO v obychnoi geometricheskoi formulirovke. Podrobnym obrazom eta svyaz' issledovana v rabote [1] s pomosh'yu slozhnoi i gromozdkoi matematiki. Zdes' my daem klyuchevye vyvody [1] i daem kachestvennye poyasneniya.

5.1.1 Smesheniya Li i preobrazovaniya Li geometricheskih ob'ektov

Opredelenie preobrazovanii Li i proizvodnyh Li mozhet byt' naideno vo mnogih uchebnikah i s raznyh pozicii, naprimer v rabote [2]. Predpolozhim, chto nekotoroe koordinatnoe preobrazovanie opredeleno smesheniem vdol' kongruencii opredelennoi vektornym polem $\xi^\alpha$ . Togda ego mozhno predstavit' v vide ryada

$\begin{displaymath} {x^\prime}^\alpha = x^\alpha + \xi^\alpha (x) + {1\over{2!}}... ...3!}} \xi^\pi (\xi^\beta \xi^\alpha_{ ,\beta})_{,\pi} + {...} \end{displaymath}$

(5.1)

gde, voobshe govorya, ne delaetsya predpolozhenii o malosti $\xi^\alpha$ i ih proizvodnyh, hotya dolzhny byt' vvedeny neobhodimye predpolozheniya o differenciruemosti. Predpolozhim, chto na 4-mnogoobrazii opredelen nekotoryi nabor geometricheskih ob'ektov $\Psi^A(x)$ . Posle preobrazovanii (5.1) poluchim $\Psi^A(x) \rightarrow \Psi'^A(x')$ . Teper' sdelaem tak nazyvaemoe tochechnoe preobrazovanie, to est' otobrazim prostranstvo-vremya samo na sebya tak chto kazhdoi tochke so znacheniem koordinat x v sisteme { x} sopostavim tochku so znacheniem koordinat x v sisteme { x'}. Posle etogo sravnim geometricheskie ob'ekty ishodnogo i otobrazhennogo prostranstv. Okazyvaetsya, chto

$\begin{displaymath} \Psi'^A(x) - \Psi^A(x) = \sum^\infty_{k=1} {1\over k!} {\pounds_\xi}^k \Psi^A, \end{displaymath}$

(5.2)

gde ${\pounds_\xi}$ -- proizvodnaya Li, opredelennaya eshe v lekcii 1.

Predpolozhim, chto drugoi geometricheskii ob'ekt $\Psi^{*B}(\Psi^{A})$ yavlyaetsya funkciei ot nabora predydushih i ih proizvodnyh, i ne yavlyaetsya yavnoi funkciei koordinat. S odnoi storony, v silu opredeleniya geometricheskogo ob'ekta na mnogoobrazii, posle tochechnogo preobrazovaniya $\Psi^{*B}$ dolzhen udovletvoryat' sootnosheniyu tipa (5.2). S drugoi storony, prostaya podstanovka (5.2) v $\Psi^{*B}(\Psi^{A})$ daet tozhe samoe sootnoshenie:

$\begin{displaymath} \Psi^{*B}(\Psi'^A(x)) - \Psi^{*B}(\Psi^A(x)) = \sum^\infty_{k=1} {1\over k!} {\pounds_\xi}^k \Psi^{*B}. \end{displaymath}$

(5.3)

5.1.2 Preobrazovaniya Li v geometricheskoi formulirovke OTO

Kovariantnye svoistva OTO formal'no sleduyut iz togo, chto lagranizhian v deistvii

$\begin{displaymath} S = {1 \over c} \int d^4x {\hat{\cal L}}^{GR} \equiv -{1 \... ... + {1 \over c} \int d^4x {\hat{\cal L}}^M (\Phi^A, g_{\mu\nu}) \end{displaymath}$

(5.4)

yavlyaetsya skalyarnoi plotnost'yu. Yavlyayas' geometricheskim ob'ektom, lagranzhian v deistvii (5.4) pri tochechnyh preobrazovaniyah izmenyaetsya takzhe kak v (5.2):

$\begin{displaymath} {\hat{\cal L}}'^{GR} = {\hat{\cal L}}^{GR} + \sum^\infty_{k=1} {1\over k!} {\pounds_\xi}^k {\hat{\cal L}}^{GR}. \end{displaymath}$

(5.5)

Lagranzhian ${\hat{\cal L}}^{GR}$ ne zavisit yavno ot koordinat, poetomu prosto podstanovka

$\displaystyle {\hat g}'^{\mu\nu}$	=	$\displaystyle \hat g^{\mu\nu} + \sum^{\infty}_{k = 1}{1\over{k!}} \hbox{$\pounds$}_\xi^k {\hat g^{\mu\nu}},$
$\displaystyle {\Phi}'^A$	=	$\displaystyle \Phi^A + \sum^\infty_{k = 1}{1\over{k!}} \hbox{$\pounds$}_\xi^k {\Phi^A}$	(5.6)

daet tot zhe rezul'tat (5.5). Poskol'ku ${\hat{\cal L}}^{GR}$ -- skalyarnaya plotnost', to lyuboi chlen v summe (5.5) yavlyaetsya divergenciei, sledovatel'no, vsya summa takzhe est' divergenciya. Izmenenie lagranzhiana na divergenciyu, kak izvestno, ne izmenyaet rezul'tatov var'irovaniya, to est' privedet k tem zhe samym uravneniyam. Poetomu chasto pri issledovanii simmetrii deistviya vmesto svoistv kovariantnosti rassmatrivayut invariantnost' otnositel'no Li preobrazovanii. Obychno ogranichivayutsya lish' pervym chlenom v summah (5.6) i sootvetstvenno v (5.5), naprimer, kak v uchebnike Landau i Lifshica [3].

5.1.3 Dinamicheskii lagranzhian

Davaite perepishem dinamicheskii lagranzhian polevoi formulirovki opredelennyi v (4.25) lekcii 4 v konkretnoi forme:

		$\displaystyle {\hat{\cal L}}^{dyn} = {\hat{\cal L}}^{GR} - {\hat{\cal L}}^{(1)} - {\hat{\cal L}}^{(0)} + div$
		$\displaystyle = {\hat{\cal L}}^{GR}\left((\overline{\hat g^{\mu\nu}} + \hat l^{... ...over {\delta \overline{\Phi^A}}}\right) - \overline{{\hat{\cal L}}^{GR}} + div.$	(5.7)

Obsudim smysl postroeniya. Yasno, chto prostaya podstanovka razbieniya

$\begin{displaymath} \hat g^{\mu\nu} \equiv \overline {\hat g^{\mu\nu}} + \hat l^{\mu\nu}, \Phi^A \equiv \overline {\Phi^A} + \phi^A \end{displaymath}$

(5.8)

v ${\hat{\cal L}}^{GR}$ k novym svoistvam ne privodit. Kak pri var'irovanii po dinamicheskim peremennym, tak i pri var'irovanii po fonovovym poluchayutsya lish' uravneniya Einshteina v prezhnei forme. Reshayushim yavlyaetsya vychitanie ${\hat{\cal L}}^{(1)}$ . S odnoi storony, var'irovanie po dinamicheskim peremennym daet te zhe uravneniya Einshteina. Deistvitel'no, chlen ${\hat{\cal L}}^{(1)}$ ne daet vklada poskol'ku on lineeen po $\hat l^{\mu\nu}$ i $\phi^A$ , i proporcionalen, kak eto vidno iz (5.7), fonovym uravneniyam, kotorye schitayutsya vypolnennymi posle var'irovaniya. S drugoi storony, blagodarya vychitaniyu ${\hat{\cal L}}^{(1)}$ var'irovanie ${\hat{\cal L}}^{dyn}$ v (5.7) po fonovoi metrike $\overline g^{\mu\nu}$ dast neischezayushii polnyi tenzor energii-impul'sa $\hat t^{(tot)}_{\mu\nu}$ (sm. (30) v lekcii 4) kak istochnik v polevyh uravneniyah. Vychitanie ${\hat{\cal L}}^{(0)}$ takzhe neobhodimo, deistvitel'no, ono garantiruet, chto v otsutstvie vsyakih polei ( $\hat l^{\mu\nu}=0$ i $\phi^A=0$ ) otsutstvuet i sam dinamicheskii lagranzhian ${\hat{\cal L}}^{dyn} =0$ .

Ostaetsya vopros, kotoryi trebuet takzhe obsuzhdeniya. Pochemu fonovye uravneniya (ih operatory vhodyat v ${\hat{\cal L}}^{(1)}$ -- sm. (5.7)) my ne schitaem vypolnennymi do var'irovaniya? Delo v tom, chto tochno takoi zhe chlen soderzhitsya v pervom slagaemom, tol'ko neyano. Deistvitel'no, ${\hat{\cal L}}^{GR}$ mozhet byt' razlozhen v ryad po dinamicheskim peremennym s pomosh'yu variacionnyh proizvodnyh. Togda stanovitsya ochevidnym, chto ryad soderzhit ${\hat{\cal L}}^{(1)}$ , no tol'ko so znakom (+) i eti chleny dolzhny vzaimno sokrashat'sya. Takoe razlozhenie kak raz pokazyvaet, chto ${\hat{\cal L}}^{dyn}$ ne menee, chem kvadratichen po $\hat l^{\mu\nu}$ i $\phi^A$ , chto estestvenno dlya obychnoi polevoi teorii.

5.1.4 Kalibrovochnye preobrazovaniya

Teper' poyasnim tu invariantnost', kotoraya byla prodeklarirovana v lekcii 4 otnositel'no preobrazovanii:

$\displaystyle {\hat l}'^{\mu\nu}$	=	$\displaystyle \hat l^{\mu\nu} + \sum^{\infty}_{k = 1}{1\over{k!}} \hbox{$\pounds$}_\xi^k \left(\overline {\hat g^{\mu\nu}} + \hat l^{\mu\nu}\right),$
$\displaystyle {\phi}'^A$	=	$\displaystyle \phi^A + \sum^\infty_{k = 1}{1\over{k!}} \hbox{$\pounds$}_\xi^k \left(\overline{\Phi^A}+\phi^A\right).$	(5.9)

Podstanovka (5.9) v pervyi iz lagranzhianov v (5.7) ekvivalentna podstanovke (5.6) v ${\hat{\cal L}}^{GR}$ s rezul'tatom (5.5), gde lanranzhian priobretaeit lish' dopolnitel'nuyu divergenciyu. Podstanovka (5.9) v chlen ${\hat{\cal L}}^{(1)}$ ostavlyaet ego proporcional'nym fonovym uravneniyam. Takim obrazom, my dokazali utverzhdenie, chto ${\hat{\cal L}}^{dyn}$ invarianten otnositel'no kalibrovochnyh preobrazovanii (5.9) s tochnost'yu do divergencii i na fonovyh uravneniyah.

Invariantnost' uravnenii dvizheniya v polevoi formulirovke otnositel'- no (5.9) ustanavlivaetsya takzhe prosto. Polevye uravneniya ekvivalentny obychnym uraneniyam Einshteina na fonovyh uravneniyah. Znachit, s tochnost'yu do fonovyh uravnenii argumenty vhodyat v operatory uravnenii tol'ko v vide summ (5.8). A togda podstanovka kalibrovochnyh preobrazolvanii (5.9) v polevye uravneniya privedet k preobrazovaniyu tipa (5.3) dlya operatorov uravnenii. A eto znachit, chto esli uravneniya dvizheniya udovletvoreny, to oni invariantny otnositel'no (5.9). Drugimi slovami, uravneniya dvizheniya polevoi formulirovki OTO invariantny otnositel'no kalibrovochnyh preobrazovanii (5.9) na samih sebe i na fonovyh uravneniyah.

Pri preobrazovaniyah (5.9) fonovaya metrika ne podvergaetsya nikakim preobrazovaniyam, koordinaty tozhe neizmenny. Znachit, (5.9) vpolne mozhno interpretirovat' kak kalibrovochnye (vnutrennie) preobrazovaniya, i zabyt', chto oni yavlyayutsya rezul'tatom smeshenii Li v geometricheskoi formulirovke i posleduyushego perehoda k polevoi.

5.1.5 Intepretaciya kalibrovochnyh preobrazovanii

My pokazali kak kalibrovochnye preobrazovaniya (5.9) v polevoi formulirovke svyazany s preobrazovaniyami Li v geometricheskoi. Okazyvaetsya, chto (5.9) takzhe svyazany s vyborom fona dlya postroeniya polevoi formulirovki. Rassmotrim nekotoroe reshenie uravnenii Einshteina $\hat g^{\mu\nu}$ i razob'em ego na summu fonovyh i dinamicheskih chastei:

$\begin{displaymath} \hat g^{\mu\nu}(x) = \overline {\hat g^{\mu\nu}}(x) + \hat l^{\mu\nu}(x). \end{displaymath}$

(5.10)

Sdelaem proizvol'noe koordinatnoe preobrazovanie, predstavimoe v vide (5.1):

$\begin{displaymath} {x^\prime}^\alpha = {x^\prime}^\alpha (x). \end{displaymath}$

(5.11)

Teper' preobrazuem vybrannoe reshenie v novye koordinaty i sdelaem razbienie

$\begin{displaymath} (\hat g'^{\mu\nu})(x') = \overline {\hat g^{\mu\nu}}(x') + \hat l'^{\mu\nu}(x'). \end{displaymath}$

(5.12)

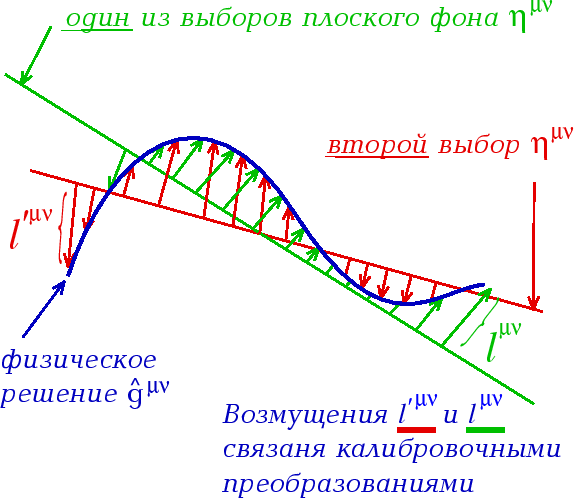
Glavnoe svoistvo etogo razbieniya v tom, chto forma fonovoi metriki ta zhe samaya, chto i v razbienii (5.10), hotya i v novyh koordinatah. Teper' v sootnoshenii (5.9) v ramkah sistemy { x'} pereidem ot tochek so znacheniyami x' k tochkam so znacheniyami x. Posle etogo, ispol'zuya (5.10) i (5.11) v forme (5.1) poluchim, chto $\hat l^{\mu\nu}(x)$ i $\hat l'^{\mu\nu}(x)$ svyazany pervym iz preobrazovanii (5.9).

Ris.3.

Vspomnim, chto i v (5.10), i v (5.12) fonovaya metrika odna i ta zhe. No poskol'ku ona vybrana v razlichnyh koordinatah, to eto oznachaet chto fonovoe prostranstvo-vremya, k kotoromu otnositsya eta metrika, vybiraetsya dvumya razlichnymi sposobami. Kazhdyi sposob opredelyaet svoi vozmusheniya, kotorye svyazany vpolne opredelennymi sootnosheniyami (5.9). Kachestvenno eta situaciya poyasnyaetsya na Ris. 3, gde krivaya oznachaet samo reshenie, a dve pryamye oznachayut vybor fona, skazhem ploskogo, dvumya razlichnymi sposobami. Otkloneniya krivoi ot kazhdoi iz pryamoi opredelyaet dva sorta vozmushenii, kotorye i svyazany kalibrovochnymi preobrazovaniyami. Takim obrazom, fiksaciya kalibrovki oznachaet fiksaciyu sposoba zadaniya fona.

Kak illyustraciyu rassmotrim reshenie Shvarcshil'da v dvuh sistemah koordinat: shvarcshil'dovoi $\{ t, R, \theta, \phi\}$ i izotropnoi $\{ t, \rho, \theta, \phi\}$ . V oboih sluchayah v kachestve fona vyberem ploskii. V pervom sluchae on opisyvaetsya sfericheskimi koordinatami $\{ t, R, \theta, \phi\}$ , vo vtorom sluchae sfericheskimi koordinatami $\{ t, \rho, \theta, \phi\}$ . V kazhdom sluchae postroim vozmusheniya, a zatem, skazhem v pervom sluchae, zamenim R na $\rho$ , togda poluchim, chto vozmusheniya etih dvuh sortov svyazany preobrazovaniyami tipa (5.9), no seichas bez yavnogo vyrazheniya cherez vektory $\xi^\alpha$ .

<< 5. Interpretaciya i prilozheniya ... | Oglavlenie | 5.2 Izolirovannye sistemy na ... >>

Publikacii s klyuchevymi slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Sm. takzhe: Padenie shara v Solnechnoi sisteme Gravitacionnye anomalii na Merkurii Galaktika Arp 94 Sputniki GRAIL sostavlyayut kartu lunnoi gravitacii 70 let Stivenu Hokingu Molotok protiv peryshka na Lune Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce