- 5.2.1 Asimptoticheski ploskoe prostranstvo-vremya
- 5.2.2 Global'nye sohranyayushiesya velichiny
- 5.2.3 Naislabeishee ubyvanie gravitacionnyh potencialov
5.2 Izolirovannye sistemy na prostrannstvennoi beskonechnosti
5.2.1 Asimptoticheski ploskoe prostranstvo-vremya
My nazyvaem prostranstvo-vremya
asimptoticheski ploskim, esli ono sootvetstvuet izolirovannoi (ostrovnoi)
sisteme v ploskom prostranstve-vremeni (sm., naprimer,
raboty [4]![]() [5]),
i v kachestve opredeleniya udovletvoryaet sleduyushim ishodnym
,,naivnym'' trebovaniyam:
[5]),
i v kachestve opredeleniya udovletvoryaet sleduyushim ishodnym
,,naivnym'' trebovaniyam:
- (1)
Na prostranstvennoi beskonechnosti mirovye tochki parametrizuyutsya
koordinatami
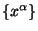 takimi, chto
takimi, chto
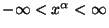 .
.
- (2)
V odnoi iz etih sistem metrika imeet povedenie:
pri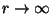 , gde
, gde
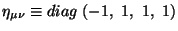 i
i
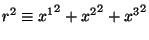 .
Oboznachenie
.
Oboznachenie 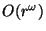 sootvetstvuet
asimptoticheskomu povedeniyu pri
sootvetstvuet
asimptoticheskomu povedeniyu pri
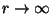 .
.
- (3)
Ne sushestvuet koordinatnyh sistem, dlya kotoryh padenie
potencialov gravitacionnogo polya bylo by bystree, chem v (5.13).
- (4) Tenzor energii-impul'sa istochnikov v sisteme (5.13) imeet
povedenie:
Pereformuliruem eto opredelenie v ramkah polevogo podhoda. Dlya etogo nuzhno vybrat' fon. My vybiraem prostranstvo Minkovskogo v lorencevyh koordinatah (5.13). Posle vybora fona vybor koordinat (v silu kovariantnosti vseh vyrazhenii polevoi formulirovki) ne vazhen, no lorencevy koordinaty zdes' udobny, poskol'ku v nih ochevidno asimptoticheskoe povedenie. Po etoi zhe prichine my ne ispol'zuem kryshki v etoi chasti lekcii. Itak, punkt (1) sohranitsya.
- (2)
V odnoi iz kalibrovok gravitacionnye potencialy imeyut povedenie:
- (3)
Ne sushestvuet kalibrovok, gde ubyvanie
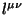 bylo by bystree, chem v (5.15).
bylo by bystree, chem v (5.15).
- (4)
Uslovie dlya material'nyh istochnikov takzhe sohranyaetsya:
5.2.2 Global'nye sohranyayushiesya velichiny
Dlya togo, chtoby opredelit' integraly dvizheniya
ostrovnoi sistemy my ispol'zuem vektory Killinga fonovogo
prostranstva Minkovskogo:
gde secheniya
gde d Sk element koordinatnogo ob'ema na ,,stenkah'' cilindra (sm. Ris. 1), okruzhayushego izolirovannuyu sistemu.
Uravneniya Einshteina v polevoi formulirovke na ploskom fone
mogut byt' perepisany v vide
(sm. (12) v lekcii 4):
Podstanovka (5.20) i (5.21) v (5.18) i ispol'zovanie antisimmetrii
gde dsi -- koordinatnyi element integrirovaniya na 2-sfere, okruzhayushei izolirovannuyu sistemu.
5.2.3 Naislabeishee ubyvanie gravitacionnyh potencialov
Podstanovka potencialov s povedeniem (5.15) v integraly dvizheniya
privodit k tomu, chto (5.22) okazyvayutsya horosho opredelennymi,
v to vremya kak (5.23) i (5.24)
rashodyatsya. Chtoby izbezhat' etogo,
dostatochno usilit' usloviya padeniya do
gde (+) i (-) oznachayut chetnuyu i nechetnuyu funkcii po otnosheniyu k izmeneniyu znaka 3-vektora
Usloviya (5.25) dolzhny byt' Puankare invariantny, poetomu
neobhodimo potrebovat' [5]
kak eto chasto trebuyut pri posleduyushih integrirovaniyah [7].
Dlya real'noi ostrovoi sistemy padenie bystree, chem v
(5.15) (ili v (5.25))
nevozmozhno v silu neobhodimosti sootvetstvovat' zakonu N'yutona
v slabopolevom priblizhenii. A vot mozhet li ono byt' slabee bez izmeneniya
osnovnyh integral'nyh harakteristik? Okazyvaetsya, chto
mozhet [7]![]() [9]
[9]![]() [5].
Chtoby opredelit' usloviya padeniya bolee slabye, chem (5.25)
my ispol'zuem
kalibrovochno invariantnye svoistva polevoi formulirovki [5].
Kak my ustanovili,
uravneniya dvizheniya kalibrovochno invariantny na samih sebe. Eto oznachaet,
chto dlya ploskogo fona polnyi tenzor energii-impul'sa
pri preobrazovaniyah (5.9) preobrazuetsya kak:
[5].
Chtoby opredelit' usloviya padeniya bolee slabye, chem (5.25)
my ispol'zuem
kalibrovochno invariantnye svoistva polevoi formulirovki [5].
Kak my ustanovili,
uravneniya dvizheniya kalibrovochno invariantny na samih sebe. Eto oznachaet,
chto dlya ploskogo fona polnyi tenzor energii-impul'sa
pri preobrazovaniyah (5.9) preobrazuetsya kak:
Vazhno otmetit', chto vyrazhenie
![]() invariantno (v absolyutnom smysle, bezotnositel'no k usloviyam padeniya)
otnositel'no
invariantno (v absolyutnom smysle, bezotnositel'no k usloviyam padeniya)
otnositel'no
chto yavlyaetsya samym pervym chlenom summy v (5.27), i, takim obrazom, bol'she ne rassmatrivaetsya.
Teper' budem iskat' ogranicheniya na povedenie ![]() .
Ispol'zuem sleduyushie ochevidnye trebovaniya:
.
Ispol'zuem sleduyushie ochevidnye trebovaniya:
- (i) Dinamicheskie polya
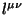 i
i 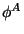 udovletvoryayut uravneniyam Einshteina i usloviyam padeniya
(5.16) i (5.25), (5.26).
udovletvoryayut uravneniyam Einshteina i usloviyam padeniya
(5.16) i (5.25), (5.26).
- (ii) Kazhdaya iz ishodnyh komponent
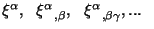 yavlyaetsya proizvol'noi nezavisimoi velichinoi v kazhdoi tochke prostranstva
Minkovskogo. Estestvenna simmetriya po nizhnim indeksam.
yavlyaetsya proizvol'noi nezavisimoi velichinoi v kazhdoi tochke prostranstva
Minkovskogo. Estestvenna simmetriya po nizhnim indeksam.
- (iii)
Velichiny
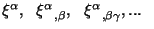 izmenyayutsya kak tenzory pri Puankare preobrazovaniyah.
izmenyayutsya kak tenzory pri Puankare preobrazovaniyah.
- (iv)
Funkcii
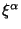 yavlyayutsya klassa
yavlyayutsya klassa
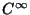 i kazhdaya sleduyushaya proizvodnaya ot
i kazhdaya sleduyushaya proizvodnaya ot 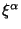 padaet bystree predydukshei na odin poryadok po stepeni
r. Takim obrazom, vse svoistva
padaet bystree predydukshei na odin poryadok po stepeni
r. Takim obrazom, vse svoistva
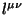 sohranyayutsya dlya
sohranyayutsya dlya
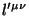 .
.
Predpolozhim usloviya padeniya dlya ![]() v forme:
v forme:
V silu punkta (ii) rassmatrivaem vse chleny tipa
Etogo usloviya dostatochno, chtoby vse ostavshiesya chleny v kalibrovochnoi summe ne davali vklada v
Kombinirovanie (5.30) i (5.31) privodit k ogranicheniyam na povedenie (5.28)
kotoroe odnovremenno garantiruet invariantnost' otnositel'no (5.9)
Takim obrazom, podstanovka (5.28) s usloviyami (5.32)
v (5.9) daet povedenie dlya
gravitacionnyh peremennyh v vide:
Asimptotika (5.33) s usloviyami (5.32)
zametno slabee, chem ishodnaya
(5.25). Tem ne menee vse integraly (5.18)
(ili v yavnom vyrazhenii --
(5.22) - (5.24))
sohranyayut svoi znacheniya. Malo togo, pri kazhdom posleduyushem
kalibrovochnom preobrazovanii (5.9) s (5.28) i
(5.32):
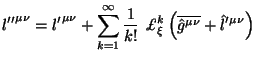 |
my uzhe ne narushim povedenie (5.33), znacheniya P(K) takzhe ostayutsya prezhnimi.
Naislabeishee asimptoticheskoe povedenie (5.33) s usloviyami
(5.32) yavlyayutsya
novymi rezul'tatami, poskol'ku oni
utochnyayut i ispravlyayut
izvestnye rezul'taty [7]![]() [9].
[9].
<< 5.1 Kalibrovochnye preobrazovaniya v ... | Oglavlenie | 5.3 Interpretaciya zadannogo fona >>
|
Publikacii s klyuchevymi slovami:
zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
![$\displaystyle {1\over{c \kappa}} {\lim_{r \rightarrow \infty}}
\int_{\Sigma} \left[ U^{\alpha 0 i}_{ ,i}\right] dx^3$](https://images.astronet.ru/pubd/2001/09/12/0001170672/img629.gif)
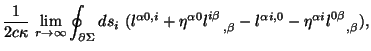
![$\displaystyle {1\over {2 c \kappa}} {\lim_{r \rightarrow
\infty}} \int_{\Sigma}{ \left [(U^{n0i} x^m - U^{m0i} x^n)_{,i} +
U^{m0n} - U^{n0m} \right]dx^3}$](https://images.astronet.ru/pubd/2001/09/12/0001170672/img632.gif)
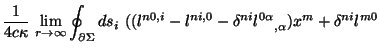
![$\displaystyle {1\over{2 c \kappa}} {\lim_{r \rightarrow \infty}}
\int_{\Sigma}{
\left[(U^{00i} x^m - U^{m0i} x^0)_{,i} - U^{00m}\right]dx^3}$](https://images.astronet.ru/pubd/2001/09/12/0001170672/img636.gif)
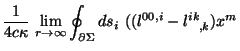
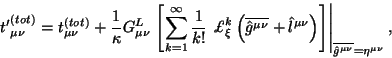
![\begin{displaymath}
O^{-}\left(
\partial_\alpha
\left[\sum^{\infty}_{k = 1}{1\ov...
...at l^{\mu\nu}\right)\right]\right)
< O^{-}\left(r^{-2}\right).
\end{displaymath}](https://images.astronet.ru/pubd/2001/09/12/0001170672/img657.gif)