Astronet > 5.3 Interpretaciya zadannogo fona v polevoi formulirovke OTO

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 5.2 Izolirovannye sistemy na ... | Oglavlenie | 5.4 Problemy interpretacii reshenii >>

Razdely

5.3 Interpretaciya zadannogo fona v polevoi formulirovke OTO

5.3.1 Nenablyudaemost' fona v polevoi formulirovke

Kak my uzhe otmechali, polevaya i geometricheskaya formulirovki OTO -- eto raznye predstavleniya odnoi i toi zhe teorii, oni ekvivalentny. Nablyudatel'nye predskazaniya dolzhny byt' odnimi i temi zhe. V OTO principial'no net nablyudaemogo fiksirovannogo prostranstva-vremeni. Deistvitel'no posle otozhdestvlenii

$\begin{displaymath} \sqrt{-g}g^{\mu\nu} \equiv \hat g^{\mu\nu} \equiv \overline ... ...u\nu}} +\hat l^{\mu\nu}, \Phi^A = \overline \Phi^A + \phi^A \end{displaymath}$

(5.34)

polevaya formulirovka perehodit v geometricheskuyu. Kak metrika $\overline { g_{\mu\nu}}$ , tak i polya $\overline \Phi^A$ ischezayut iz rassmotreniya. Otozhdestvlenie (5.34) govorit o tom, chto fonovye polya ne uchastvuyut vo vzaimodeistviyah nezavisimo ot dinamicheskih, takim obrazom -- eto ukazanie, chto fonovye polya ne nablyudaemy.

Kak prosledit' naglyadno (fizicheski) chto fon deistvitel'no nenablyudaem (sm. podrobnee rabotu [10])? Predpolozhim, chto prostranstvo Minkovskogo vybrano v kachestve fona. V prostranstve Minkovskogo bez vsyakoi gravitacii svetovoi signal dvizhetsya po pryamym, ego skorost' i chastota stabil'ny. Tem samym metricheskie svoistva fona opredelyayutsya odnoznachno standartnymi procedurami s ispol'zovaniem sveta. V prisutstvii gravitacionnyh polei $\hat l^{\mu\nu}$ skorost' svetovyh signalov i chastota izmenyaetsya. Togda izmerenie rasstoyanii stanovitsya sil'no zavisimym ot $\hat l^{\mu\nu}$ , to est' prostranstvo Minkovskogo perestaet byt' nablyudaemym s pomosh'yu svetovyh signalov.

Ono takzhe perestaet byt' nablyudaemym, esli popytat'sya opredelit' izmereniya s pomosh'yu gravitacionno-volnovogo signala. Rassmotrim polevye uravneniya polevoi formulirovki na ploskom fone

$\begin{displaymath} \hat G^L_{\mu\nu}(l) = \kappa \left( \hat t^{gr}_{\mu\nu} + \hat t^{m}_{\mu\nu}\right) \end{displaymath}$

(5.35)

s levoi chast'yu

$\begin{displaymath} 2\hat G^L_{\mu\nu}(l) \equiv \overline D^\alpha_{ \alpha} \h... ...l^\alpha_{ \mu} - \overline D_{\alpha\mu}\hat l^\alpha_{ \nu}. \end{displaymath}$

(5.36)

V neobhodimoi kalibrovke v levoi chasti (5.35), kak vidno iz (5.36), mozhet ostat'sya lish' operator Dalambera $\overline D^\alpha_{ \alpha}$ . Tem samym, kazalos' by, opredelenie prostranstva Minkovskogo garantirovano. No ,,ne vse karty otkryty''! Neobhodimo uchityvat' samodeistvie v pravoi chasti (5.35). Sredi vseh chlenov tam soderzhatsya takzhe chleny tipa $\sqrt{-\bar g} l^{\alpha\beta} l^{\mu\nu}_{ ,\alpha\beta}$ , kotorye ochevidno iskazhayut dalambertian prostranstva Minkovskogo i delayut eto prostranstvo nenablyudaemym.

5.3.2 Zamknutaya model' Fridmana v terminah polevoi formulirovki

Zdes', na primere zamknutoi Vselennoi Fridmana my pokazhem, chto ploskii fon mozhno ispol'zovat' v samyh kazalos' by nedopustimyh situaciyah, kogda topologiya fonovogo i fizicheskogo prostranstva-vremeni ne sovpadayut. S odnoi storony, my prodemonstriruem uslovnost' takogo vybora fona, s drugoi storony, nesmotrya na eto ispol'zovanie polevoi formulirovki privodit k vpolne osmyslennym rezul'tatam [11].

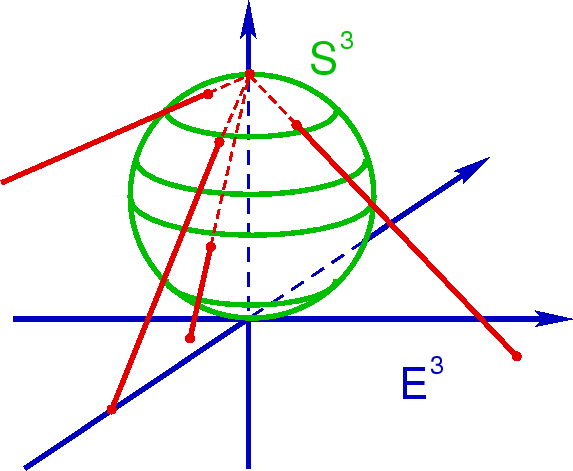
Ris.4. Stereograficheskaya proekciya

Metriku zamknutogo mira predstavim v vide:

$\begin{displaymath} ds^2 = - c^2 dt^2 + {a^2 \over {1+r^2/4}} \left(d{x^1}^2 + d{x^2}^2 +d {x^3}^2\right). \end{displaymath}$

(5.37)

Dlya postroeniya polevoi konfiguracii vybiraem fon kak prostranstvo Minkovskogo s lorencevymi koordinatami v (5.37) i razbienie: $\hat g^{\mu\nu} = {\eta^{\mu\nu}} + l^{\mu\nu}.$ Togda nenulevye komponenty polevoi konfiguracii imeyut znacheniya:

$\begin{displaymath} l^{00} = 1 - \left({a^2 \over {1+r^2/4}}\right)^3, l^{11} = l^{22} = l^{33} = {a^2 \over {1+r^2/4}} -1. \end{displaymath}$

(5.38)

Takaya konfiguraciya sootvetstvuet tak nazyvaemoi stereograficheskoi proekcii 3-sfery na ploskoe 3-prostranstvo (Ris. 4). ,,Nizhnii'' polyus sfery sootvetstvuet nachalu koordinat, ,,verhnii'' polyus otozhdestvlyaetsya srazu so vsemi tochkami na formal'noi beskonechnosti ploskogo mira. Takim obrazom topologiya 3-sfery S³ kak by ,,uproshaetsya'' do topologii ploskogo prostranstva E³. Pole (5.38) formal'no zaponyaet beskonechnyi ob'em. Esli zhe proizvodit' fizicheski razumnye izmereniya s pomosh'yu real'nyh svetovyh signalov v gravitacionnom pole, to pridem k standartnomu znacheniyu ob'ema 3-sfery.

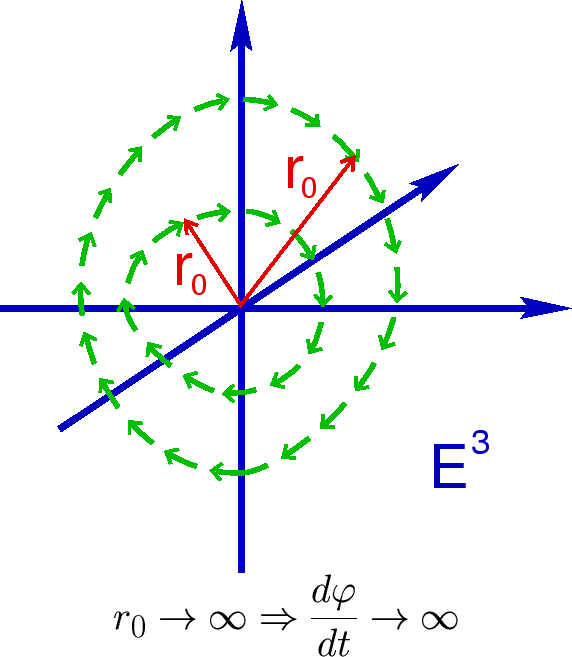
Ris.5.

Uslovnost' vybrannogo fona podcherkivaetsya takzhe sleduyushim myslennym eksperimentom. Predstav'te, chto v prostranstve Minkovskogo, zapolennom polem (5.38) luchi sveta dvizhutsya po okruzhnostyam s centrom v nachale koordinat (Ris. 5). Svobodno svet ne mozhet dvigat'sya takim obrazom, no kartina mozhet byt' smodelirovana s pomosh'yu sistemy zerkal i predel'noi procedury. Togda v sfericheskoi sisteme koordinat uravnenie takoi ,,geodezicheskoi'' imeet vid

$\displaystyle \theta$	=	$\displaystyle \theta_0 = const,$
r	=	r₀ = const,
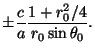$\displaystyle {d\phi \over dt}$	=	$\displaystyle \pm {c\over a} {{1+ r^2_0/4}\over {r_0\sin \theta_0}}.$

Kak vidno, pri $r_0 \rightarrow \infty$ ,,uglovaya'' skorost' sveta stanovitsya beskonechnoi i dlya prohozhdeniya polnoi okruzhnosti na beskonechnosti vremeni sovsem ne trebuetsya. Pri vozvrashenii k fizicheskomu prostranstvu-vremeni vse stanovitsya na svoi mesta, poskol'ku vsya prostranstvennaya beskonechnost' prostranstva Minkovskogo sootvetsvuet odnoi edinstvennoi tochke -- ,,verhnemu'' polyusu 3-sfery.

Nesmotrya na uslovnost' ploskogo fona v ramkah zamknutoi modeli Fridmana, konfiguraciya (5.38) imeet vpolne fizicheskuyu interpretaciyu. Deistvitel'no, poschitaem dlya nee integraly dvizheniya (5.18), opredelyayushie global'nye sohranyayushiesya velichiny v prostranstve Minkovskogo. My poluchim vse 10 velichin ravnymi nulyu. Eto kak raz soootvetstvuet vozmozhnomu kvantovomu rozhdeniyu zamknutogo mira iz ,,nichego'' [12].

<< 5.2 Izolirovannye sistemy na ... | Oglavlenie | 5.4 Problemy interpretacii reshenii >>

Publikacii s klyuchevymi slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Sm. takzhe: Padenie shara v Solnechnoi sisteme Gravitacionnye anomalii na Merkurii Galaktika Arp 94 Sputniki GRAIL sostavlyayut kartu lunnoi gravitacii 70 let Stivenu Hokingu Molotok protiv peryshka na Lune Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce