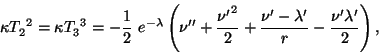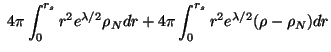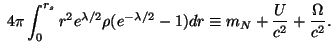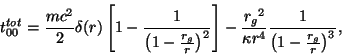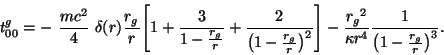Astronet > 5.4 Nekotorye problemy interpretacii reshenii OTO

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 5.3 Interpretaciya zadannogo fona | Oglavlenie | Literatura k Lekcii 5 >>

Razdely

5.4 Nekotorye problemy interpretacii reshenii OTO

Interpretaciya reshenii yavlyaetsya odnoi iz vazhnyh sostavlyayushih chastei lyuboi fizicheskoi teorii. Narlikarom [13] byli opisany trudnosti, kotorye vstrechayutsya pri opisanii raspredeleniya mass i energii shvarcshil'dova resheniya v obychnoi geometricheskoi formulirovke OTO. My privodim nizhe eti argumenty. Zatem, v ramkah polevoi formulirovki, pokazyvaem, chto eti interpretacionnye (mozhno skazat' metodicheskie) trudnosti stanovyatsya nesushestvennymi.

5.4.1 Problemy interpretacii shvarcshil'dova resheniya

My predstavlyaem problemy, sleduya rabote [13]. Vypishem sfericheski simmetrichnyi element dlya staticheskoi sistemy v obshem sluchae:

$\begin{displaymath} ds^2 = e^\nu c^2 dt^2 - e^\lambda dr^2 - r^2 (d{{\theta}^2} + {{\sin^2}{\theta}} d{\phi^2}). \end{displaymath}$

(5.39)

Uravneniya Einshteina priobretayut vid [3]:

$\begin{displaymath} \kappa T^{ 0}_0 = - e^{-\lambda}\left ({1 \over {r^2}} - {{{\lambda}^\prime} \over r}\right) + {1 \over {r^2}}, \end{displaymath}$

(5.40)

$\begin{displaymath} \kappa T^{ 1}_1 = - e^{-\lambda}\left ({1 \over {r^2}} + {{{\nu}^\prime} \over r}\right) + {1 \over {r^2}}, \end{displaymath}$

(5.41)

$\begin{displaymath} \kappa T^{ 2}_2 = \kappa T^{ 3}_3 = - {1 \over 2} e^{-\lambd... ...e} \over r} - {{{\nu^\prime}{\lambda^\prime}} \over 2}\right), \end{displaymath}$

(5.42)

gde $\lambda = \lambda(r)$ , $\nu = \nu(r)$ i $(^\prime) \equiv d/{dr}$ . V pustom prostranstve uraneniya (5.40) - (5.42) imeyut reshenie

$\begin{displaymath} \nu + \lambda = 0, e^{-\lambda} = 1 - {B \over r}, B = const. \end{displaymath}$

(5.43)

Dlya vybora postoyannoi B predpolagaetsya, chto na prostransvennoi beskonechnosti gravitacionnye effekty slaby i delaetsya sravnenie s n'yutonovym zakonom tyagoteniya: $B = {{2mG} /{c^2}} \equiv {r_g}.$ Togda podstanovka (5.43) v (5.39) i daet izvestnoe reshenie Shvarcshil'da. Strogo govorya, takoe opredelenie B svyazano ne tol'ko s gravitiruyushei massoi, no i s ,,massoi'' gravitacionnogo polya, kotoroe v ramkah OTO dolzhno ,,vesit''', a udalennyi nablyudatel' mozhet chuvstvovat' tol'ko massu vsei sistemy v celom -- tela i gravitacionnogo polya.

Snachala opishem PERVUYu iz problem rassmotrennyh v rabote [13]. Povtorim uprazhnenie predlozhennoe v knige [3], to est' perepishem uravnenie (5.40) v vide


		$\displaystyle {d \over {dr}}\left [r \left(1 - e^{-\lambda}\right)\right] = \kappa r^2 c^2 T^{ 0}_0 = 8 \pi G r^2 \rho$

i prointegriruem ego po ob'emu do poverhnosti sfericheskogo tela s radiusom r = r_s:

$\begin{displaymath} m \equiv {m(r_s)} = {4\pi}\int^{r_s}_0 { r^2\rho(r)dr}. \end{displaymath}$

(5.44)

Takoe opredelenie massy ne tak estestvenno, kak kazhetsya s pervogo vzglyada. Prezhde vsego, ob'emnyi element dlya giperpoverhnosti t = const v metrike (5.39) ne budet bol'she kak v ploskom mire $4\pi{r^2}dr$ , a na samom dele est' $4\pi{r^2}{e^{\lambda/2}}dr$ . Landau i Lifshic [3] interpretiruyut etot fakt kak defekt mass. Odnako etot vyvod delaetsya lish' na osnovanii togo, chto znachenie integrala (5.44) men'she, chem moglo by byt' pri integrirovanii po $4\pi{r^2}{e^{\lambda/2}}dr$ bez ob'yasnenii. Krome togo, integrirovanie v (5.44) vypolnyaetsya do r = r_s, (to est' vsya massa m opredelyaetsya lish' materiei), v to vremya kak postoyannaya B byla fakticheski opredelena materiei s inducirovannym ei gravitacionnym polem, kak my eto otmetili. To, chto ob'yasnenie s pomosh'yu defekta mass malo obosnovano ponimayut davno. Poetomu v knige [14] predlozhena drugaya traktovka formuly (5.44):

m	=	$\displaystyle 4\pi \int^{r_s}_0 {r^2e^{\lambda/2}\rho_Ndr} + 4\pi \int^{r_s}_0 {r^2e^{\lambda/2}(\rho - \rho_N)dr}$
	+	$\displaystyle 4\pi \int^{r_s}_0 {r^2e^{\lambda/2}\rho(e^{-\lambda/2} - 1)dr} \equiv {m_N +{U \over {c^2}} + {\Omega \over {c^2}}}.$	(5.45)

Zdes' m_N traktuetsya kak nuklonnaya massa tela, kak esli by ono bylo postroeno iz svobodnyh gravitacionno nevzaimodeistvuyushih chastic s plotnost'yu $\rho_N$ . Velichina U opredelyaetsya kak vnutrennyaya energiya s plotnost'yu $\rho - \rho_N$ , i, nakonec, $\Omega$ nazyvaetsya gravitacionnoi potencial'noi energiei. Nazvanie sleduet iz togo, chto v slabopolevom priblizhenii


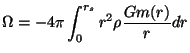		$\displaystyle \Omega = -4\pi\int^{r_s}_0{r^2\rho{{Gm(r)} \over r}dr}$

i nahoditsya v sootvetstvii s n'yutonovoi potencial'noi energiei. No izmenennaya formula (5.45) takzhe ne bez iz'yanov, Bondi, eshe v rabote [15], otmechal, chto chlen m_N ne yavlyaetsya invariantnym.

VTORAYa problema rassmotrennaya Narlikarom [13] kasaetsya problemy tochechnoi massy. V n'yutonovoi gravitacii takaya problema reshaetsya prosto. Sama po sebe ona zvuchit tak: Kak opisyvat' tochechnuyu massu, esli my zhelaem, chtoby n'yutonov potencial m/r imel smysl vezde, vklyuchaya tochku r =0? Dlya etogo dostatochno predpolozhit', chto raspredelenie mass zadaetsya v vide $m\delta(r)$ , gde $\delta$ -funkciya udovletvoryaet obychnomu uravneiyu Puassona


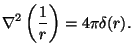		$\displaystyle \nabla^2 \left({1\over r}\right) = 4\pi\delta(r).$

Malo togo, kak pri obychnom regulyarnom raspredelenii $\rho(x)$ , tak i pri raspredelenii dlya tochechnoi chasticy $\rho(x) = m\delta(r)$ , polnaya massa sistemy raschityvaetsya s pomosh'yu odnogo i togo zhe integrala:


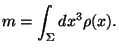		$\displaystyle m = \int_\Sigma dx^3 \rho(x).$

Esli my popytaemsya v OTO, ispol'zuya Shvarcshil'dovo reshenie, opisat' tochechnuyu massu, my vstretim konceptual'nye trudnosti. Predpolozhim, chto reshenie (5.43) imeet mesto vo vsem prostranstve-vremeni, vklyuchaya mirovuyu liniyu r=0, togda material'noe raspredelenie budet opisyvat'sya komponentami tenzora energii-impul'sa:

$\begin{displaymath} T^{ 0}_0 = T^{ 1}_1 = 0, T^{ 2}_2 = T^{ 3}_3 = {{mc^2} \over 2} \delta(r). \end{displaymath}$

(5.46)

Dlya takogo raspredeleniya nevozmozhno poluchit' korrektnuyu massu sistemy integrirovaniem tipa (5.44).

5.4.2 Reshenie metodicheskih problem v ramkah polevoi formulirovki

Dve otmechennye problemy vyglyadyat kak metodicheskie, tem ne menee oni ne razreshayutsya v ramkah geometricheskoi formulirovki OTO. My ih razreshaem s pomosh'yu polevogo podhoda [16].

Dlya resheniya (5.39) vyberem ploskii fon v koordinatah etogo zhe resheniya:

$\begin{displaymath} \bar g_{00} = 1, \bar g_{11} = -1, \bar g_{22} = - r^2, \bar g_{33} = - r^2 {\sin^2}\theta. \end{displaymath}$

(5.47)

Togda v silu razbieniya $\hat g^{\mu\nu} =\sqrt{-\bar g}(\bar g^{\mu\nu}+ l^{\mu\nu})$ nenulevye komponenty gravitacionngogo polya prinimayut vid:

l⁰⁰	=	$\displaystyle e^{(\lambda - \nu)/2} - 1, l^{11} = 1 - e^{(\nu -\lambda)/2},$
l²²	=	$\displaystyle r^{-2}\left(1 - e^{(\nu +\lambda)/2}\right), l^{33} = r^{-2} {\sin^{-2}}\theta\left(1 - e^{(\nu +\lambda)/2}\right).$	(5.48)

Otmetim, chto esli $\nu +\lambda = 0$ -- eto obychnoe reshenie Shvarcshil'da v vakuume, esli $\nu +\lambda \neq 0$ , to eto reshenie v prisutstvii materii.

Integral energii s sootvetstvuyushim vektorom Killinga (sm. (5.18)) v koordinatah (5.47) priobretaet vid:

$\begin{displaymath} E^{tot} = \lim_{r \rightarrow \infty} \int_{\Sigma}{d^3x\sqrt{-\bar g^{(3)}} t^{00}_{(tot)}}, \end{displaymath}$

(5.49)

gde t⁰⁰_(tot) -- plotnost' raspredeleniya energii obychnoi materii i gravitacionnogo polya. V silu vypolneniya uravnenii Einshteina (5.20) etot integral perepisyvaetsya v vide poverhnostnogo:

$\begin{displaymath} E^{tot} = {1 \over {2 \kappa}} \lim_{r \rightarrow \infty} \... ...\left(l^{00}\bar g^{ij} + l^{ij}\bar g^{00}\right)_{\vert i}}, \end{displaymath}$

(5.50)

gde vertikal'naya cherta -- kovariantnaya proizvodnaya po prostranstvennoi metrike v (5.47). Esli est' neobhodimost', to integrirovanie kak v (5.49), tak i v (5.50) mozhet byt' ogranicheno lyuboi sferoi r = r₀.

V sluchae integrirovaniya vnutri materii (5.49), my delaem predpolozhenie, chto raspredelenie dostatochno regulyarno, chtoby bylo dopustimo integrirovanie. Chtoby poluchit' znachenie integrala mass, kak vidno iz (5.50), dostatochno znat' znacheniya gravitacionnyh potencialov (5.48) na granice -- net neobhodimosti znat' yavnye znacheniya material'nyh peremennyh dlya vychisleniya (5.49), dostatochno znat' chto oni udovletvoryayut uravneniyam Einshteina. Tak, dlya sfericheski simmetrichnoi ostrovnoi sistemy integral (5.50) dlya polnoi massy daet estestvennyi rezul'tat mc². V lyubom sluchae, uravnenie (5.49) reshaet PERVUYu metodicheskuyu problemu, deistvitel'no v (5.49) my integriruem v ploskom prostranstve i imeem pravil'nyi element integrirovaniya $d^3x\sqrt{-\bar g^{(3)}}$ .

Teper' pereidem ko VTORO' probleme -- probleme tochechnoi massy. Pole (5.48) v vakkume imeet vid:

$\begin{displaymath} h^{00} = {{r_g} \over r} {1 \over {1 - {{r_g} \over r}}}, h^{11} = {{r_g} \over r}. \end{displaymath}$

(5.51)

My predpolagaem, chto eto reshenie spravedlivo takzhe na mirovoi linii r=0. Dlya (5.51), vklyuchaya mirovuyu liniyu r=0, formuly polevoi formulirovki pozvolyayut poschitat' polnuyu plotnost' energii

$\begin{displaymath} t^{tot}_{00} = {{mc^2} \over 2} \delta (r)\left[1 - {1 \ove... ... {\kappa r^4}} {1 \over {\left(1 - {{r_g}\over r}\right)^3}}, \end{displaymath}$

(5.52)

kotoraya razbivaetsya na material'nuyu i gravitacionnuuyu chasti:

$\begin{displaymath} t^m_{00} = - {{mc^2}\over 4} \delta(r) \left[1 - {{r_g}\over r} - {1 \over {1 - {{r_g} \over r}}}\right], \end{displaymath}$

(5.53)

$\begin{displaymath} t^g_{00} = - {{mc^2}\over 4} \delta(r) {{r_g} \over r} {\le... ...{\kappa r^4}} {1 \over {\left(1 - {{r_g}\over r}\right)^3}}. \end{displaymath}$

(5.54)

Formuly (5.52) - (5.54), mozhet byt' ne tak izyashno kak v n'yutonovoi gravitacii, no vpolne razumno (v otlichie ot geometricheskoi formulirovki) predstavlyayut plotnost' massy dlya tochechnoi chasticy v OTO. Malo togo, podstanovka plotnosti energii t^tot₀₀ iz (5.52) v integral mass (5.49) vpolne dopustimo i pryamoe integrirovanie daet ozhidaemyi rezul'tat mc². Takim obrazom vtoraya metodicheskaya problema takzhe reshaetsya v ramkah polevogo formalizma.

<< 5.3 Interpretaciya zadannogo fona | Oglavlenie | Literatura k Lekcii 5 >>

Publikacii s klyuchevymi slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Sm. takzhe: Padenie shara v Solnechnoi sisteme Gravitacionnye anomalii na Merkurii Galaktika Arp 94 Sputniki GRAIL sostavlyayut kartu lunnoi gravitacii 70 let Stivenu Hokingu Molotok protiv peryshka na Lune Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce