Astronet > 1.1 Klassicheskie psevdotenzory i superpotencialy: kratkaya istoriya, nekotorye svoistva i problemy

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 1. Teorema Neter: psevdotenzory ... | Oglavlenie | 1.2 Superpotencial Kaca-Krushciela ... >>

Razdely

1.1 Klassicheskie psevdotenzory i superpotencialy: kratkaya istoriya, nekotorye svoistva i problemy

1.1.1 Psevdotenzor Einshteina

Rassmatrivaya problemu energii gravitacionnogo polya i, v chastnosti, gravitacionnyh voln, Einshtein [1] vpervye dlya postroeniya zakonov sohraneniya v OTO predlozhil psevdotenzor energii-impul'sa gravitacionnogo polya. On konstruiruetsya sleduya opredeleniyu kanonicheskogo tenzora energii-impul'sa v obychnoi polevoi teorii. Vmesto kovariantnogo lagranzhiana ispol'zuetsya tak nazyvaemyi usechennyi nekovariantnyi lagranzhian Einshteina:

$\begin{displaymath} {\hat{\cal L}}^E = - \frac {1}{2\kappa} \hat g^{\mu\nu}\left... ...\nu} - \Gamma^\rho_{\mu\nu} \Gamma^\sigma_{\rho\sigma}\right), \end{displaymath}$

(1.1)

kotoryi otlichaetsya ot kovariantnogo lagranzhiana Gilberta na divergenciyu, blagodarya chemu privodit k tem zhe uravneniyam. V (1.1) i dalee: $\kappa$ -- postoyannaya Einshteina; grecheskie indeksy yavlyayutsya chetyrehmernymi i probegayut znacheniya 0, 1, 2, 3; $\Gamma^\rho_{\mu\nu}$ -- simvoly Kristoffelya; kryshka nad simvolami oznachaet, chto velichina yavlyaetsya plotnost'yu vesa +1 (naprimer, eto mozhet byt' dostignuto umnozheniem tenzora, ili dazhe psevdotenzora, na $\sqrt{-g}$ ). (Chasto, na protyazhenii vseh lekcii, chtoby ne zagromozhdat' tekst, my opuskaem slovo ,,plotnost''', poskol'ku iz formul tochnyi matematicheskii smysl velichin ocheviden.) Preimushestvo lagranzhiana (1.1) zaklyuchaetsya v tom, chto on zavisit ot metriki $g_{\mu\nu}$ i tol'ko ee pervyh proizvodnyh. Po standartnym pravilam postroeniya kanonicheskogo tenzora energii-impul'sa konstruiruetsya ob'ekt, sootvetstvuyushii lagranzhianu (1.1):

$\begin{displaymath} \hat t_\nu^{E\mu} = {\frac{\partial {\hat{\cal L}}^E} {\part... ...\partial_\nu g_{\alpha\beta} -\delta^\mu_\nu {\hat{\cal L}}^E. \end{displaymath}$

(1.2)

Eto i est' psevdotenzor Einshteina. Iz analiza lagranzhiana (1.1) sleduet differencial'nyi zakon sohraneniya

$\begin{displaymath} \partial_\mu \hat t_\nu^{E\mu} = 0, \end{displaymath}$

(1.3)

kotoryi, sobstvenno, yavlyaetsya uravneniem nepreryvnosti:

$\begin{displaymath} \partial_0 \hat t_\nu^{E0} + \partial_k \hat t_\nu^{Ek} = 0, \end{displaymath}$

(1.4)

gde latinskie indeksy otvechayut prostranstvennym koordinatam k = 1, 2, 3.

1.1.2 Superpotencial Tolmena

Zakon sohraneniya (1.3) vypolnyaetsya pri vypolnennyh uravneniyah Einshteina v vakuume. Eto oznachaet, chto pri

$\begin{displaymath} \hat G_\nu^{\mu}= 0 \end{displaymath}$

(1.5)

uravnenie (1.3) vypolnyaetsya tozhdestvenno: $\partial_\mu \hat t_\nu^{E\mu} \equiv 0$ . No togda psevdotenzor Einshteina dolzhen vyrazhat'sya cherez nekotoruyu velichinu $\hat {\cal T}^{\mu\alpha}_\nu$ so svoistvom $\partial_{\mu\alpha}\hat {\cal T}^{\mu\alpha}_\nu \equiv 0$ sleduyushim obrazom:

$\begin{displaymath} \hat t_\nu^{E\mu} \equiv \partial_\alpha \hat {\cal T}^{\mu\alpha}_\nu. \end{displaymath}$

(1.6)

Obychno superpotencialom nazyvayut velichinu, dvoinaya divergenciya kotoroi tozhdestvenno obrashaetsya v nul'. Superpotencial $\hat {\cal T}^{\mu\alpha}_\nu$ , sootvetstvuyushii psevdotenzoru Einshteina byl naiden Tolmenom [2] v nachale 30-h i imeet yavnyi vid:

$\begin{displaymath} \hat {\cal T}^{\mu\alpha}_\nu = \frac{\sqrt{-g}} {2\kappa} \... ...- \delta^\alpha_{(\rho} \Gamma^\sigma_{\lambda)\sigma}\right). \end{displaymath}$

(1.7)

Dlya nevakuumnogo sluchaya tozhdestvo (1.6) perehodit v tozhdestvo

$\begin{displaymath} \frac{1}{\kappa} \hat G_\nu^{\mu} + \hat t_\nu^{E\mu} \equiv \partial_\alpha \hat {\cal T}^{\mu\alpha}_\nu, \end{displaymath}$

(1.8)

kotoroe pri vypolnennyh uravneniyah Einshteina perehodit v uravnenie

$\begin{displaymath} \hat T_\nu^{\mu} + \hat t_\nu^{E\mu} = \partial_\alpha \hat {\cal T}^{\mu\alpha}_\nu. \end{displaymath}$

(1.9)

Fakticheski eto drugaya forma uravnenii Einshteina. Iz (1.9) neslozhno videt', chto dlya nevakuumnyh reshenii OTO vmesto (1.3) nuzhno ispol'zovat' differencial'nyi zakon sohraneniya:

$\begin{displaymath} \partial_\mu \left(\hat T_\nu^{\mu} + \hat t_\nu^{E\mu}\right) =0. \end{displaymath}$

(1.10)

1.1.3 Superpotencial Freida

Kak pravilo, v kachestve superpotencialov ispol'zuyut antisimmetrichnye velichiny, tak chto stanovitsya ochevidnym tozhdestvennoe ravenstvo nulyu dvoinoi divergencii ot nih. Superpotencial Tolmena (1.7) ne obladaet etim svoistvom. V rezul'tate voznikayut neudobstva pri ispol'zovanii, slozhnosti pri kovariantizacii. Uluchshit' situaciyu udalos' Freidu [3]. Zarannee predpolagaya antisimmetriyu superpotenciala $\hat F^{\mu\alpha}_\nu = - \hat F^{\alpha\mu}_\nu$ , sootvetstvuyushego einshteinovskomu psevdotenzoru, vmesto uravneniya (1.9) on predlozhil

$\begin{displaymath} \hat T_\nu^{\mu} + \hat t_\nu^{E\mu} = \partial_\alpha \hat F^{\mu\alpha}_\nu \end{displaymath}$

(1.11)

s yavnoi formoi superpotenciala:

$\begin{displaymath} \hat F^{\mu\alpha}_\nu \equiv \frac{1}{2\kappa}\frac{g_{\nu... ...^{\alpha\lambda} - g^{\mu\lambda}g^{\alpha\rho}\right)\right]. \end{displaymath}$

(1.12)

Kazalos' by sushestvuet protivorechie mezhdu (1.9) i (1.11). V deistvitel'nosti ono vidimoe, poskol'ku $\partial_\alpha \hat F^{\mu\alpha}_\nu \equiv \partial_\alpha \hat {\cal T}^{\mu\alpha}_\nu$ blagodarya tomu, chto mezhdu superpotencialami sushestvuet svyaz'


		$\displaystyle \hat F^{\mu\alpha}_\nu \equiv \hat {\cal T}^{\mu\alpha}_\nu + \pa... ...��{\rm s}�� \partial_{\alpha\beta} \hat {\Phi}^{\mu\alpha\beta}_\nu \equiv 0.$

1.1.4 Vopros edinstvennosti i procedura Neter

Dazhe imeya v rasporyazhenii vpolne opredelennyi psevdotenzor my tol'ko chto ubedilis' v neopredelennosti postroeniya superpotencialov. Rassmotrim problemu edinstvennosti zakonov sohraneniya, takih kak (1.3) ili (1.10), podrobnee. Ispol'zuya metriku i ee pervye proizvodnye postroim proizvol'nym obrazom velichinu $\hat U^{\mu\alpha}_\nu$ , potrebuem tol'ko, chtoby ona udovletvoryala tozhdestvu $\partial_{\mu\alpha}\hat U^{\mu\alpha}_\nu \equiv 0$ . Zatem opredelim velichinu

$\begin{displaymath} \hat \theta^{\mu}_\nu = \partial_{\alpha}\hat U^{\mu\alpha}_\nu -\frac{1}{\kappa} \hat G^{\mu}_\nu. \end{displaymath}$

(1.13)

No eto oznachaet, chto uravneniya Einshteina mogli by byt' perepisany v forme:

$\begin{displaymath} \hat T_\nu^{\mu} + \hat \theta_\nu^{\mu} = \partial_\alpha \hat {U}^{\mu\alpha}_\nu, \end{displaymath}$

(1.14)

gde $\hat U^{\mu\alpha}_\nu$ igraet rol' superpotenciala, a $\hat \theta_\nu^{\mu}$ -- novogo psevdotenzora. Vmesto (1.10) differencial'nyi zakon sohraneniya priobretaet, voobshe govorya, sovershenno proizvol'nuyu formu:

$\begin{displaymath} \partial_\mu \left(\hat T_\nu^{\mu} + \hat \theta_\nu^{\mu}\right) =0. \end{displaymath}$

(1.15)

Takaya neopredelennost' v zakonah sohraneniya ne mozhet byt' udovletvoritel'noi. Odnako formula (1.2) ukazyvaet, chto opredelenie psevdotenzora, v principe, moglo by byt' svyazano s vyborom lagranzhiana. Issledovanie etoi problemy bylo provedeno detal'no, ei udelili vnimanie takie avtory kak Bergman [4], Goldberg [5], Moller [6], Trautman [7], Mickevich [8]. Kratko rezul'taty etih usilii svodyatsya k sleduyushemu. Nesmotrya na to, chto lagranzhian (1.1) ne yavlyaetsya obshekovariantnym, -- on invarianten otnositel'no lineinyh prebrazovanii. Eto pozvolyaet dlya translyacii opredelennyh vektorom $\xi^\mu = \delta^\mu_{(\alpha)}$ napisat' tozhdestvo Neter:

$\begin{displaymath} {\pounds_\xi} {\hat{\cal L}}^E + \partial_\mu \left(\xi^\mu {\hat{\cal L}}^E\right) \equiv 0, \end{displaymath}$

(1.16)

gde ${\pounds_\xi}$ -- proizvodnaya Li vdol' vektornogo polya $\xi^\alpha$ , nashe opredelenie kotoroi sovpadaet s opredeleniem Mickevicha [8]. Pryamoi, mozhet byt' gromozdkii pereschet privodit (1.16) k vidu:

$\begin{displaymath} \partial_\mu \left(\frac{1}{\kappa} \hat G_\nu^{\mu} + \hat t_\nu^{E\mu}\right) \equiv 0, \end{displaymath}$

(1.17)

kotoryi pri ispol'zovanii uravnenii Einshteina daet zakon sohraneniya (1.10). Takim obrazom:

V smysle procedury Neter, einshteinovskii psevdotenzor (1.2) edinstvenno opredelyaetsya einshteinovskim lagranzhianom (1.1).
Esli lagranzhiany razlichayutsya na divergenciyu: 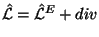${\hat{\cal L}} = {\hat{\cal L}}^E + div$ , to oni (hotya i privodyat k odnim i tem zhe uravneniyam dvizheniya) dayut razlichnye psevdotenzory.

1.1.5 Superpotencial Mollera

Takim obrazom, svoboda v vybore psevdotenzora v principe ne ogranichivaetsya -- ona perehodit v svobodu vybora lagranzhiana. To est' tak ili inache, chtoby poluchit' opredelennyi rezul'tat neobhodimo ispol'zovat' dopolnitel'nye ,,razumnye'' trebovaniya pri postroenii psevdotenzorov i superpotencialov. Trebovaniya Mollera [6] pri postroenii ego psevdotenzora $\hat {\cal M}^\mu_\nu$ i superpotenciala $\hat \chi^{\mu\alpha}_{\nu}$ sleduyushie:

(I) Dlya izolirovannyh sistem 4-impul's vsei sistemy na prostranstvennoi beskonechnosti

$\begin{displaymath} {\cal P}_\nu = {1\over \kappa} \int_\Sigma {\hat {\cal M}^0_... ...M}^\mu_\nu \equiv \partial_\alpha \hat \chi^{\mu\alpha}_{\nu}; \end{displaymath}$ (1.18)

dolzhen preobrazovyvat'sya kak svobodnyi 4-vektor pri lineinyh koordinatnyh preobrazovaniyah.
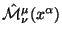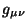(II) $\hat {\cal M}^\mu_\nu(x^\alpha)$ dolzhen algebraicheski zaviset' ot metriki $g_{\mu\nu}$ i proizvodnyh ot nee do vtorogo poryadka.
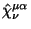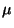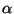(III) $\hat \chi^{\mu\alpha}_{\nu}$ dolzhen byt' antisimmetrichnym po $\mu$ i $\alpha$ i zaviset' ot 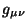$g_{\mu\nu}$ i tol'ko ee pervyh proizvodnyh.
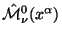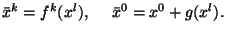
(IV) Komponenty $\hat {\cal M}^0_\nu(x^\alpha)$ dolzhny preobrazovyvat'sya kak 4-vektornaya plotnost' po otnosheniyu k chisto prostranstvennym preobrazovaniyam: $\bar x^k = f^k(x^l),��\bar x^0 = x^0 + g(x^l).$

Vazhno zametit', chto superpotencial Freida (1.12) ne udovletvoryaet trebovaniyu (IV). V kachestve ishodnogo ravenstva Moller bral zakon sohraneniya (1.10), dobavlyal k nemu $\partial_\mu \hat a^\mu_\nu \equiv 0$ i podbiral $\hat a^\mu_\nu$ tak, chtoby udovletvorit' (I) - (IV). V rezul'tate uravneniya Einshteina priobretayut vid:

$\begin{displaymath} \hat T_\nu^{\mu} + \hat {\cal M}_\nu^{\mu} = \partial_\alpha \hat {\chi}^{\mu\alpha}_\nu \end{displaymath}$

(1.19)

s yavnoi formoi superpotenciala:

$\begin{displaymath} \hat {\chi}^{\mu\alpha}_\nu = {1\over 2\kappa} \sqrt{-g} g^{... ...\partial_\beta g_{\nu\rho} -\partial_\rho g_{\nu\beta}\right). \end{displaymath}$

(1.20)

Okazalos', chto psevdotenzor v (1.19) i superpotencial (1.20) sootvetstvuyut (v smysle procedury Neter) kovariantnomu lagranzhianu Gilberta

${\hat{\cal L}}^H = - ({1/2\kappa}) \hat R$ .

1.1.6 Nekovariantnost' psevdotenzorov i sootvetstvuyushie problemy

Nekovariantnye velichiny v fizike voobshe malo zhelatel'ny. Odnako OTO zanimaet osoboe polozhenie, poskol'ku prostanstvo-vremya (v kotorom proishodyat vzaimodeistviya) samo yavlyaetsya dinamicheskim ob'ektom. V silu principa ekvivalentnosti nevozmozhno postroit' lokal'nuyu plotnost' energii gravitacionnogo polya. V rezul'tate etogo i poyavlyayutsya nekovariantnye psevdotenzory, znacheniya kotoryh v kazhdoi tochke mogut but' obrasheny v nul' koordinatnymi preobrazovaniyami.

Krome togo, chto differencial'nye zakony sohraneniya polezny v lokal'nom smysle (eto uravneniya nepreryvnosti), oni neobhodimy dlya postroeniya tak nazyvaemyh global'nyh zakonov sohraneniya. Esli v differencial'nyh zakonah (takih kak (1.3), (1.4) ili (1.10)) ispol'zovanie psevdotenzorov vyglyadit bolee ili menee estestvenno, to pri postroenii global'nyh zakonov na nekotorye trudnosti prihoditsya zakryvat' glaza. Eto vynuzhdennyi shag pri nalichii psevdotenzorov, on chasto vstrechaetsya v uchebnikah, v chastnosti v zamechatel'nom uchebnike Landau i Lifshica [9]. Seichas my proanaliziruem situaciyu.

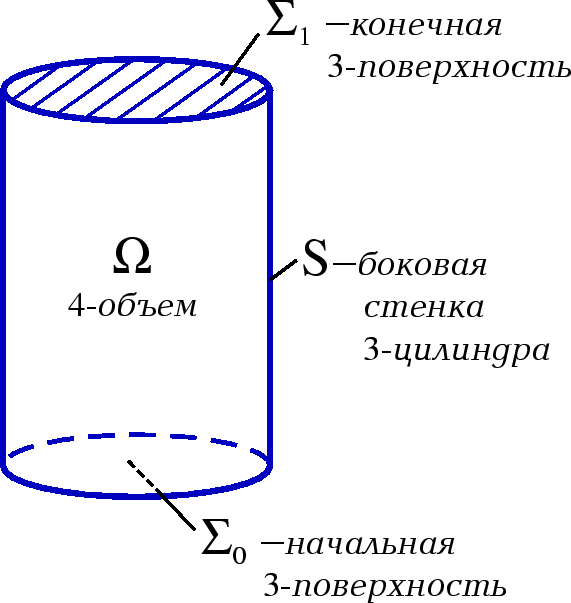
Ris.1.

V prostranstve-vremeni rassmatrivaetsya 4-mernyi ob'em $\Omega$ , ogranichennyi cilindrom s prostranstvennopodobnymi secheniyami ${\Sigma}_0$ i ${\Sigma}_1$ , i bokovoi vremenipodobnoi stenkoi S (Ris. 1). Pust' my imeem v rasporyazhenii differencial'nyi zakon sohraneniya dlya nekotorogo psevdotenzora $\hat \theta^\mu_\nu$ :

$\begin{displaymath} \partial_\mu \hat \theta^\mu_\nu = 0. \end{displaymath}$

(1.21)

Kak pravilo, snachala (1.21) prosto integriruetsya po $\Omega$ :

$\begin{displaymath} \int_\Omega\partial_\mu \hat \theta^\mu_\nu d^4 x = 0, \end{displaymath}$

(1.22)

a zatem ispol'zuetsya obobshennaya teorema Gaussa

$\begin{displaymath} \int_{\Sigma_1} \hat \theta^0_\nu d^3 x - \int_{\Sigma_0} \hat \theta^0_\nu d^3 x + \oint_{S} \hat \theta^\mu_\nu dS_\mu = 0, \end{displaymath}$

(1.23)

gde dlya $\Sigma$ ispol'zovalos' opredelenie: t = x⁰ = const. Uravnenie (1.23) kak raz opredelyaet global'nyi (zaklyuchennyi v 3-prostranstve $\Sigma$ , ogranichennom ili neogranichennom) 4-impul's

$\begin{displaymath} {\cal P}_\nu = \int_{\Sigma} \hat \theta^0_\nu d^3 x. \end{displaymath}$

(1.24)

Esli poslednii integral v (1.23) ischezaet, to 4-impul's (1.24) sohranyaetsya; esli poslednii integral v (1.23) ne ischezaet, to on opredelyaet potok cherez bokovuyu stenku cilindra i ${\cal P}_\nu$ izmenyaetsya v zavisimosti ot etogo.

Kritika (1.21) - (1.24) ochevidna: 1) nel'zya integrirovat' nekovariantnye velichiny, 2) nel'zya integrirovat' velichiny s koordinatnymi indeksami. Odnako, nesmotrya na ubiistvennnost' argumentov situaciya mozhet byt' spasena.

1.1.7 Kovariantizaciya psevdotenzorov i korrektnye zakony sohraneniya

Chtoby kovariantizovat' psevdotenzory nuzhno predstavit', chto sushestvuet vspomogatel'noe prostranstvo Minkovskogo, a vse velichiny zapisany v lorencevyh koordinatah. (Togda pri perehode k proizvol'nym koordinatam chastnye proizvodnye estestvennnym obrazom perehodyat v kovariantnye.) Takim obrazom, nuzhno schitat', chto v nekovariantnyh formulah ,,zapryatana'' metrika Minkovsogo $\eta_{\mu\nu}$ i ee opredelitel' $\eta \equiv \det{\eta_{\mu\nu}} = -1$ .

Zamechanie: Ispol'zovanie dopolnitel'nogo zadannogo prostranstva-vremeni v teorii, gde ego fakticheski ne sushestvuet, kazhetsya, nedopustimym. Odnako, ochen' mnogie zadachi v OTO, -- kak chisto teoreticheskie, tak i raschety eksperimentov, -- kak raz ispol'zuyut eto predpolozhenie. Sam harakter zadach trebuet ispol'zovaniya fona. Konechno vnutrennyaya soglasovannost' OTO ne narushaetsya -- uravneniya Einshteina ostayutsya uravneniyami Einshteina.

Neobhodimo takzhe izbavit'sya ot integrirovaniya vektornyh velichin. V obychnyh polevyh teoriyah sohranyayushiesya integraly sootvetstvuyut simmetriyam prostranstve-vremeni, v kotorom eti teorii rassmatrivayutsya. Davaite i teper' ispol'zovat' vektory translyacii Killinga $\xi^\rho_{(\nu)} = \delta^\rho_{\nu}$ uzhe vvedennogo vspomogatel'nogo prostranstva Minkovskogo, gde nizhnii indeks est' lish' nomer vektora Killinga, eto ne koordinatnyi indeks.

Posle etih predpolozhenii (1.21) perepisyvaetsya v ekvivalentnoi forme:


		$\displaystyle \partial_\mu \left[\sqrt{-\eta} \left({\hat \theta^\mu_\rho} / {\sqrt{-\eta}} \right) \xi^\rho_{(\nu)}\right] = 0,$

gde sleva, ochevidno, skalyarnaya plotnost', kotoraya bez problem integriruetsya po 4-ob'emu:


		$\displaystyle \int_\Omega \partial_\mu \left[\sqrt{-\eta} \left({\hat \theta^\mu_\rho} / {\sqrt{-\eta}}\right) \xi^\rho_{(\nu)}\right] d^4 x = 0,$

chto privodit k korrektnomu opredeleniyu 4-impul'sa na sechenii $\Sigma := x^0 = const$ :


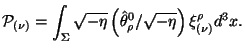		$\displaystyle {\cal P}_{(\nu)} = \int_{\Sigma}\sqrt{-\eta} \left(\hat \theta^0_\rho / {\sqrt{-\eta}}\right) \xi^\rho_{(\nu)}d^3 x.$

Analiziruya poslednie tri formuly, mozhno sdelat' vyvod, chto sam psevdotenzor igraet lish' vspomogatel'nuyu rol'. Na samom dele ,,differencial'no'' sohranyaetsya vektornaya plotnost' (tok):

$\begin{displaymath} \hat J^\mu(\xi) = \sqrt{-\eta} \left({\hat \theta^\mu_\rho} ... ...ght) \xi^\rho_{(\nu)}��:= �� \partial_\mu \hat J^\mu(\xi) = 0, \end{displaymath}$

(1.25)

kotoraya i uchastvuet v postroenii global'noi sohranyayusheisya velichiny, sootvetstvuyushei vektoru Killinga $\xi^\alpha$ :

$\begin{displaymath} {\cal P}(\xi) = \int_{\Sigma} \hat J^0(\xi)d^3 x. \end{displaymath}$

(1.26)

<< 1. Teorema Neter: psevdotenzory ... | Oglavlenie | 1.2 Superpotencial Kaca-Krushciela ... >>

Publikacii s klyuchevymi slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Sm. takzhe: Padenie shara v Solnechnoi sisteme Gravitacionnye anomalii na Merkurii Galaktika Arp 94 Sputniki GRAIL sostavlyayut kartu lunnoi gravitacii 70 let Stivenu Hokingu Molotok protiv peryshka na Lune Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce