Astronet > 1.2 Superpotencial Kaca-Krushciela -- obobshennyi superpotencial Freida

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 1.1 Klassicheskie psevdotenzory i ... | Oglavlenie | 1.3 Postroenie sohranyayushihsya tokov ... >>

Razdely

1.2 Superpotencial Kaca-Krushciela -- obobshennyi superpotencial Freida

Narisovannaya vyshe kartina o zakonah sohraneniya v OTO trebuet svoego obobsheniya i razvitiya. Kakie zhe momenty dolzhny byt' uchteny? My by opredelili ih tak:

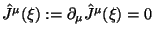(i) Zakony sohraneniya i sohranyayushiesya velichiny dolzhny opredelyat'sya sohranyayushimsya tokom (vektornoi plotnost'yu): $\hat J^\mu(\xi) := \partial_\mu \hat J^\mu (\xi) = 0$ .
(ii) Postroenie 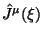$\hat J^\mu(\xi)$ opredelyaetsya lavgranzhianom i proceduroi Neter.
(iii) Model' dolzhna byt' kovariantnoi na vybrannom fone.
(iv) Zakony sohraneniya dolzhny ,,rabotat''' na proizvol'no iskrivlennyh fonah. Etogo trebuyut zadachi relyativistskoi astrofiziki ili kosmologii, gde chasto ispol'zuyutsya geometrii chernyh dyr ili kosmologicheskie resheniya, kak zadannye fony.
(v) Mozhet okazat'sya poleznym obobshenie na proizvol'nye 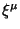$\xi^\mu$ , naprimer, v rabotah [10] 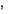$^{\!, }$ [11] ispol'zuyutsya konformnye vektory Killinga kosmologicheskogo resheniya Fridmana, a ne prostye vektory Killinga.
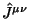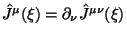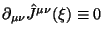(vi) Dlya sohranyayushegosya toka dolzhen byt' postroen sootvetstvuyushii antisimmetrichnyi superpotencial $\hat J^{\mu\nu}$ , tak chto $\hat J^\mu(\xi) = \partial_\nu \hat J^{\mu\nu} (\xi)$ i $\partial_{\mu\nu} \hat J^{\mu\nu} (\xi) \equiv 0$ . Stanovitsya ochevidnym differencial'nyi zakon sohraneniya, krome togo, sohranyayushiesya integraly estestvennym obrazom preobrazuyutsya v poverhnostnye.
(vii) Konechno, skonstruirovannye zakony i uchastvuyushie v nih velichiny dolzhny udovletvoryat' vsem, tak nazyvaemym, ,,estestvennym'' testam. Eto, kak minimum:
- Polozhitel'nost' plotnosti energii gravitacionnyh voln;
- Pravil'noe otnoshenie massy k uglovomu momentu v reshenii Kerra;
- Pravil'nye znacheniya global'nyh integralov dlya ostrovnoi sistemy
na prostranstvennoi beskonechnosti,
na nulevoi beskonechnosti.

Otmetim, chto punkt (vii) my ne budem podrobno obsuzhdat' v etih lekciyah. Pri neobhodimosti budem lish' otmechat' udovletvoryaet ili net obsuzhdaemaya model' etim estestvennym testam.

1.2.1 Zakony sohraneniya Kaca-Bichaka-Linden-Bella

Kac, Bichak i Linden-Bell [12] (dalee my oboznachaem etu rabotu kak KBL) predlozhili takie zakony sohraneniya, kotorye udovletvoryayut predlozhennym trebovaniyam. Postroenie osnovyvaetsya na lagranzhiane

$\begin{displaymath} {\hat{\cal L}}_G = -{1\over 2\kappa} \left(\hat R - \overline {\hat R} + \partial_\mu \hat k^\mu \right). \end{displaymath}$

(1.27)

Zdes' i dalee ispol'zuyutsya oboznacheniya: $g_{\mu\nu}$ - fizicheskaya metrika; $\bar g_{\mu\nu}$ - fonovaya metrika s sootvetstvuyushei kovariantnoi proizvodnoi $\overline D_\mu$ ; cherta sverhu nad simvolom vezde oznachaet fonovuyu velichinu;

$\hat R = \sqrt{-g} R$ i $\overline {\hat R} = \sqrt{-\bar g}\overline R$ ;

$\hat k^\mu = \hat g^{\mu\rho} \Delta^\sigma_{\rho\sigma} - \hat g^{\rho\sigma} \Delta^\mu_{\rho\sigma}$ , $\Delta^\mu_{\rho\sigma} = \Gamma^\mu_{\rho\sigma}- \overline{ \Gamma^\mu_{\rho\sigma}}$ .

Lagranzhian (1.27) obobshaet dlya proizvol'nyh fonov izvestnyi kovariantnyi lagranzhian Rozena na ploskom fone [13]. Esli zhe $\bar g_{\mu\nu} \rightarrow \eta_{\mu\nu}$ , togda $\overline D_\mu \rightarrow \partial_\mu$ i (1.27) perehodit tochno v einshteinovsii usechennyi lagranzhian (1.1).

Posledovatel'noe prilozhenie procedury Neter k lagranzhianu (1.27) s proizvol'nym $\xi^\mu$ : ${\pounds_\xi} {\hat{\cal L}}_G + \partial_\mu \left(\xi^\mu {\hat{\cal L}}_G\right) \equiv 0$ dalo vozmozhnost' postroit' sohranyayushiisya tok $\hat J^\mu(\xi)$ i superpotencial $\hat J^{\mu\nu}(\xi)$ s sootvetstvuyushim differencial'nym zakonom sohraneniya:

$\begin{displaymath} \partial_\mu \hat J^\mu (\xi) \equiv 0, \end{displaymath}$

(1.28)

$\begin{displaymath} \hat J^\mu(\xi) = \partial_\nu \hat J^{\mu\nu} (\xi). \end{displaymath}$

(1.29)

Poskol'ku (1.28) pryamo sleduet iz (1.29), to sootnosheniya tipa poslednego my chasto takzhe nazyvaem zakonami sohraneniya.

1.2.2 Superpotencial Kaca-Krushciela

Superpotencialy igrayut ochen' vazhnuyu rol' v opredelenii sohranyayushihsya velichin. Destvitel'no, davaite podstavim znachenie toka (1.29) v (1.26) i uchtem antisimmetriyu $\hat J^{\mu\nu}(\xi)$ :

$\begin{displaymath} {\cal P}(\xi) = \int_{\Sigma} \hat J^0(\xi)d^3 x = \oint_{\partial\Sigma} \hat J^{0k}(\xi)ds_k, \end{displaymath}$

(1.30)

to est' my poluchili, chto sohranyayushiisya integral predstavlyaetsya v vide poverhnostnogo integrala po granice $\Sigma$ .

Superpotencial v vyrazhenii KBL (1.29) byl poluchen ran'she nezavisimo Kacem [14] i Krushcielom [15]. Togda on byl postroen dlya bolee prostyh sistem, tem ne menee bolee slozhnaya model' razrabotannaya KBL ne izmenila ego vid:

$\begin{displaymath} {\hat J^{\mu\nu}(\xi)} ={1\over \kappa}\big({D^{[\mu}\hat \x... ...hat \xi^{\nu]}}\big)+ {1\over \kappa}\hat \xi^{[\mu} k^{\nu]}. \end{displaymath}$

(1.31)

Esli $\bar g_{\mu\nu} \rightarrow \eta_{\mu\nu}$ , a vektor $\xi^{\mu}$ vybrat' kak killingovskii vektor translyacii v prostranstve Minkovskogo, to ${\hat J^{\mu\nu}(\xi)}$ perehodit v superpotencial Freida (1.12).

1.2.3 Sohranyayushiisya tok KBL

Sohranyayushayasya vektornaya plotnost' (tok KBL) v tozhdestve (1.28) imeet vid:

$\begin{displaymath} \hat J^\mu(\xi) = \hat \Theta^\mu_\nu \xi^\nu + \hat \sigma^{\mu\rho\sigma}\overline D_{\rho}\xi_{\sigma}+ \hat Z^\mu(\xi). \end{displaymath}$

(1.32)

Ego struktura sleduyushaya. Obobshennyi tenzor energii-impul'sa imeet vid:

$\begin{displaymath} \hat \Theta^\mu_\nu = \left(\hat T^\mu_\nu - \overline {\hat... ...ight) \overline R_{\rho\sigma}\delta^\mu_\nu + \hat t^\mu_\nu, \end{displaymath}$

(1.33)

kotoryi tozhe nuzhno opisat' po chastyam. Pervoe slagaemoe predstavlyaet vozmushenie material'nogo tenzora energii-impul'sa po otnosheniyu k fonovomu, vtoroe -- ,,potencial'noe'' vzaimodeistvie s fonovoi geometriei, a tret'e est' tenzor energii-impul'sa gravitacionnogo polya:

$\displaystyle 2\kappa \hat t^\mu_\nu$	=	$\displaystyle \hat g^{\rho\sigma} \left(\Delta^\lambda_{\rho\lambda} \Delta^\mu... ...mbda_{\lambda\nu} - 2\Delta^\mu_{\rho\lambda} \Delta^\lambda_{\sigma\nu}\right)$
	-	$\displaystyle \hat g^{\rho\sigma} \left(\Delta^\eta_{\rho\sigma} \Delta^\lambda... ...\rho_{\lambda\nu} - \Delta^\sigma_{\lambda\sigma} \Delta^\rho_{\rho\nu}\right).$	(1.34)

Esli $\bar g_{\mu\nu} \rightarrow \eta_{\mu\nu}$ , to $\hat t^\mu_\nu$ perehodit v psevdotenzor Einshteina.

Vtoroi chlen v (1.32) -- tak nazyvaemyi spinovyi chlen:

$\displaystyle 2\kappa \hat \sigma^{\mu\rho\sigma}$	=	$\displaystyle (g^{\mu\rho} \overline g^{\sigma\nu} +\overline g^{\mu\sigma} g^{\rho\nu} - g^{\mu\nu} \overline g^{\rho\sigma})\hat \Delta^\lambda_{\nu\lambda}$
	-	$\displaystyle (g^{\nu\rho} \overline g^{\sigma\lambda} +\overline g^{\nu\sigma}... ...ambda} - g^{\nu\lambda} \overline g^{\rho\sigma}) \hat \Delta^\mu_{\nu\lambda}.$	(1.35)

Eta velichina sama po sebe takzhe izvestna davno. Popytka postroit' sohranyayushiisya uglovoi moment s pomosh'yu psevdotenzora Einshteina privela Papapetrou [16] k neobhodimosti ispol'zovat' vyrazhenie (1.35).

Struktura poslednego chlena v (1.32) slozhnaya i ne tak vazhna zdes', odnako mozhno skazat', chto $\hat Z^\mu(\xi)$ ischezaet dlya killingovyh vektorov fona.

Podvedem nekotoryi itog. Velichiny KBL sootvetstvuyut vsem sformulirovannym trebovaniyam (i) - (vii). Eto nesomnennoe dostoinstvo modeli. Odnako, vopros edinstvennosti dolzhen byt' obsuzhden bolee podrobno. On mozhet byt' razdelen na dve chasti:

a) Naskol'ko odnoznachen vybor lagranzhiana (1.27)?

b) Naskol'ko odnoznachny KBL velichiny pri uzhe vybrannom lagranzhiane (1.27)?

Punkt a) detal'no obsuzhdalsya v rabotah [17] $^{\!, }$ [18]. Vyvod takoi, chto trebovanie ispol'zovat' pri var'irovanii granichnye usloviya Dirihle edinstvennym obrazom privodyat k (1.27) i superpotencialu (1.31). Tam zhe obsuzhdayutsya preimushestva uslovii Dirihle. Nezavisimo, razvivaya kovariantnuyu Gamil'tonovu formulirovku gravitacionnyh teorii, k etomu zhe vyvodu prishli avtory raboty [19]. Sluduyushaya chast' lekcii, c odnoi storony, obobshaet rezul'taty KBL (v tom smysle, chto konstruiruyutsya zakony sohraneniya dlya proizvol'noi polevoi teorii so vspomolatel'nym fonom). Eto pozvolyaet otvetit' na vopros punkta b). S drugoi storony, rezul'taty sleduyushei chasti odnovremenno est' obobshenie na proizvol'no iskrivlennyi fon rezul'tatov Mickevicha [8], kotoryi skonstruiroval sohranyayushiesya velichiny dlya proizvol'noi teorii, no na ploskom fone.

<< 1.1 Klassicheskie psevdotenzory i ... | Oglavlenie | 1.3 Postroenie sohranyayushihsya tokov ... >>

Publikacii s klyuchevymi slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Sm. takzhe: Padenie shara v Solnechnoi sisteme Gravitacionnye anomalii na Merkurii Galaktika Arp 94 Sputniki GRAIL sostavlyayut kartu lunnoi gravitacii 70 let Stivenu Hokingu Molotok protiv peryshka na Lune Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce