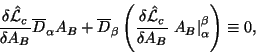- 1.3.1 Obobshennyi tok
- 1.3.2 Obobshennyi superpotencial
- 1.3.3 Vklad ot divergencii v lagranzhiane
- 1.3.4 Neopredelennost' i edinstvennost' v opredelenii tokov i superpotencialov
- 1.3.5 Edinstvennost' tokov i superpotencialov v opredelenii KBL
1.3 Postroenie sohranyayushihsya tokov i superpotencialov na proizvol'nom vspomogatel'nom fone. Problema edinstvennosti
Rassmotrim proizvol'nuyu kovariantnuyu teoriyu s lagranzhianom [20]
(snachala on v neyavno kovariantnom vide):
![]() ,
gde AB -- eto nabor dinamicheskih peremennyh,
proizvol'nyh tenzornyh plotnostei.
Vneshnee zadannoe fonovoe prostranstvo-vremya vvedem prostoi
tozhdestvennoi zamenoi:
,
gde AB -- eto nabor dinamicheskih peremennyh,
proizvol'nyh tenzornyh plotnostei.
Vneshnee zadannoe fonovoe prostranstvo-vremya vvedem prostoi
tozhdestvennoi zamenoi:
![]() .
Togda lagranzhian perepishetsya v yavno kovariantnoi forme:
.
Togda lagranzhian perepishetsya v yavno kovariantnoi forme:
Poskol'ku lagranzhian (1.36) -- eto skalyarnaya plotnost', sostavlyaem dlya nego tozhdestvo Neter:
gde koefficienty odnoznachno opredeleny lagranzhianom sleduyushim obrazom:
1.3.1 Obobshennyi tok
Podrobnyi analiz (1.38) daet drugoe sil'noe tozhdestvo:
Vyrazhenie pod divergenciei v etom tozhdestve vpolne mozhet byt' interpretirovano kak obobshennyi tok:
a samo tozhdestvo Neter (1.43) perepisyvaetsya v vide:
1.3.2 Obobshennyi superpotencial
Perepishem tozhdestvo (1.43) v vide:
Sama forma tozhdestva (1.45) govorit o tom, chto obobshennyi tok dolzhen vyrazhat'sya v vide:
gde superpotencial v pravoi chasti tozhdestvenno udovletvoryaet:
Uchet tret'ego iz tozhdestv (1.47) govorit, chto superpotencial (1.49) yavno antisimmetrichen.
1.3.3 Vklad ot divergencii v lagranzhiane
Prostym, no ochen' vazhnym yavlyaetsya vopros
o vklade v tok i superpotencil ot divergencii v lagranzhiane.
Otvet byl dan eshe Kacem [14]. Zdes' my kratko daem
rezul'tat.
Poskol'ku
![]() takzhe yavlyaetsya skalyarnoi
plotnost'yu, to dlya etoi dobavki otdel'no vypolnyaetsya tozhdestvo Neter:
takzhe yavlyaetsya skalyarnoi
plotnost'yu, to dlya etoi dobavki otdel'no vypolnyaetsya tozhdestvo Neter:
![]() ,
prostoi analiz kotorogo privodit k dobavkam v koefficientah
(1.39) - (1.41) i v superpotenciale (1.49):
,
prostoi analiz kotorogo privodit k dobavkam v koefficientah
(1.39) - (1.41) i v superpotenciale (1.49):
Neobhodimo otmetit', chto forma etih dobavok nikak ne zavisit ot struktury vektornoi plotnosti
1.3.4 Neopredelennost' i edinstvennost' v opredelenii tokov i superpotencialov
Horosho izvestno, chto bez izmeneniya tozhdestva (1.45)
k toku ![]() mozhet byt' dobavlena proizvol'naya velichina
mozhet byt' dobavlena proizvol'naya velichina
![]() , lish' by divergenciya ot nee
tozhdestvenno obrashalas' v nul':
, lish' by divergenciya ot nee
tozhdestvenno obrashalas' v nul':
![]() .
Odnako, ,,isporchennyi'' tok tem zhe samym sposobom
mozhet byt' ,,ispravlen''. Velichina
.
Odnako, ,,isporchennyi'' tok tem zhe samym sposobom
mozhet byt' ,,ispravlen''. Velichina
![]() ne svyazana s lagranzhianom i proceduroi Neter.
S drugoi storony, v opredelenii
(1.44) vse koefficenty (1.39) - (1.41)
strogo opredeleny lagranzhianom,
zadannym v obshei (neyavnoi) forme. V formule (1.44) net ni odnogo chlena
divergenciya ot kotorogo yavno by obrashalas' v nul'.
Tozhdestvo (1.45) vypolnyaetsya kak vse vyrazhenie v celom,
kak i dolzhno byt' dlya edinogo sohranyayushegosya toka Neter.
Takim obrazom, mozhno sdelat' utverzhdenie:
ne svyazana s lagranzhianom i proceduroi Neter.
S drugoi storony, v opredelenii
(1.44) vse koefficenty (1.39) - (1.41)
strogo opredeleny lagranzhianom,
zadannym v obshei (neyavnoi) forme. V formule (1.44) net ni odnogo chlena
divergenciya ot kotorogo yavno by obrashalas' v nul'.
Tozhdestvo (1.45) vypolnyaetsya kak vse vyrazhenie v celom,
kak i dolzhno byt' dlya edinogo sohranyayushegosya toka Neter.
Takim obrazom, mozhno sdelat' utverzhdenie:
- Tok (1.44) --
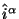 -- v smysle procedury Neter
opredelyaetsya edinstvennnym obrazom lagranzhianom teorii.
-- v smysle procedury Neter
opredelyaetsya edinstvennnym obrazom lagranzhianom teorii.
Podobnye vyvody spravedlivy i dlya opredeleniya superpotenciala
(1.49). V principe, bez izmeneniya toka ![]() k superpotencialu
v (1.48) mozhet byt' dobavlena proizvol'naya velichina
k superpotencialu
v (1.48) mozhet byt' dobavlena proizvol'naya velichina
![]() ,
lish' by divergenciya ot nee
tozhdestvenno obrashalas' v nul':
,
lish' by divergenciya ot nee
tozhdestvenno obrashalas' v nul':
![]() .
Odnako, eta dobavka nikak ne svyazana s lagranzhianom i proceduroi Neter.
Kak ee dobavili, tochno takzhe legko unichtozhit'.
S drugoi storony, v opredelenii (1.49) vse chleny strogo
opredeleny lagranzhianom i opisannoi proceduroi --
ih nevozmozhno otkinut'. Poetomu my delaem utverzhdenie:
.
Odnako, eta dobavka nikak ne svyazana s lagranzhianom i proceduroi Neter.
Kak ee dobavili, tochno takzhe legko unichtozhit'.
S drugoi storony, v opredelenii (1.49) vse chleny strogo
opredeleny lagranzhianom i opisannoi proceduroi --
ih nevozmozhno otkinut'. Poetomu my delaem utverzhdenie:
- Superpotencial (1.49) --
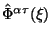 --
v smysle procedury Neter
opredelyaetsya edinstvennnym obrazom lagranzhianom teorii.
--
v smysle procedury Neter
opredelyaetsya edinstvennnym obrazom lagranzhianom teorii.
Sdelav eto utverzhdenie, my, krome togo, proillyustriruem, chto
dvusmyslennost' v superpotenciale ne opasna, vo vsyakom
sluchae dlya postroeniya global'nyh
sohranyayushihsya velichin.
Tak, tozhdestvo
![]() v svoyu ochered' govorit o tom, chto dobavka dolzhna byt' vyrazhena kak
v svoyu ochered' govorit o tom, chto dobavka dolzhna byt' vyrazhena kak
![]() , gde
, gde
![]() .
Sochetanie trebovaniya kovariantnosti i neobhodimosti ispol'zovat'
chastnye proizvodnye dlya postroeniya zakonov sohraneniya i global'nyh velichin
privodit k tomu, chto velichina
.
Sochetanie trebovaniya kovariantnosti i neobhodimosti ispol'zovat'
chastnye proizvodnye dlya postroeniya zakonov sohraneniya i global'nyh velichin
privodit k tomu, chto velichina
![]() , to est'
dolzhna byt' antisimmetrichna po vsem
indeksam. Teper' perepishem zakon sohraneniya (1.48) v izmenennom vide:
, to est'
dolzhna byt' antisimmetrichna po vsem
indeksam. Teper' perepishem zakon sohraneniya (1.48) v izmenennom vide:
chto daet vozmozhnost' postroit' sohranyayushiesya velichiny analogichno (1.30):
![$\displaystyle {\cal P}(\xi) =
\int_{\Sigma} \hat i^0(\xi)d^3 x =
\oint_{\partia...
...[\hat \Phi^{[0n]}(\xi)+
\partial_m \left(\hat j^{[0nm]}(\xi)\right)\right]ds_n.$](https://images.astronet.ru/pubd/2001/09/12/0001170672/img149.gif) |
V silu teremy Stoksa poslednii chlen ne daet vklada v integral i, takim obrazom, ne izmenyaet velichinu
1.3.5 Edinstvennost' tokov i superpotencialov v opredelenii KBL
Vernemsya k voprosu b) v konce predydushei chasti o edinstvennosti
velichin v opredelenii KBL. Prezhde vsego obsudim lagranzhian (1.27).
Perepishem skalyarnuyu kriviznu v yavno ,,kovariantizovannom'' vide:
gde, napomnim,
![]() i
i
![]() .
.
S uchetom togo, chto my znaem kakoi vklad dayut divergencii (sm. (1.50)), lagranzhian (1.27) yavlyaetsya kak raz togo vida, chto i lagranzhian (1.36) v etoi chasti. Sledovatel'no, lagranzhian (1.27) mozhet byt' podstavlen v obshie formuly etoi chasti. Pryamaya podstanovka pokazyvaet, chto vse formuly KBL poluchayutsya etim putem. Tak, podstanovka (1.27) v obobshennyi tok (1.44) daet KBL tok (1.32). Bolee detal'no: Podstanovka v koefficient (1.39) i uchet uravnenii Einshteina daet tenzor energii-impul'sa (1.33). Podstanovka v (1.40) daet spinovyi koefficient (1.35). Podstanovka v (1.41) daet tochno Z-chlen v (1.32). (Neobhodimo tol'ko uchityvat' raznicu znakov v formulah (1.39) - (1.41) i v opredelenii toka (1.44).) Takoe zhe sootvetstvie i mezhdu superpotencialami: (1.49) perehodit tochno v (1.31). Iz skazannogo ostaetsya sdelat' vyvod:
- Rezul'taty KBL opredeleny odnoznachno v smysle procedury Neter lagranzhianom modeli (1.27).
<< 1.2 Superpotencial Kaca-Krushciela ... | Oglavlenie | Literatura k lekcii 1 >>
|
Publikacii s klyuchevymi slovami:
zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
![$\displaystyle \left[{{\delta {\hat{\cal L}}_c} \over {\delta A_B}} \overline D_...
...} \over {\delta A_B}} \left.A_B\right\vert^\beta_\alpha\right)\right]\xi^\alpha$](https://images.astronet.ru/pubd/2001/09/12/0001170672/img106.gif)
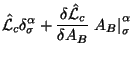
![$\displaystyle \left[{{\partial {\hat{\cal L}}_c} \over {\partial (\overline D_\...
...ine D_\beta \overline D_\alpha A_{B})}}\right) \right]
\overline D_\sigma A_{B}$](https://images.astronet.ru/pubd/2001/09/12/0001170672/img111.gif)
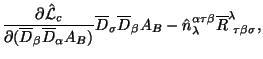
![$\displaystyle \left[{{\partial {\hat{\cal L}}_c} \over {\partial (\overline D_\...
...ta \overline D_\alpha A_{B})}}\right)\right]
\left.A_{B}\right\vert^\tau_\sigma$](https://images.astronet.ru/pubd/2001/09/12/0001170672/img114.gif)
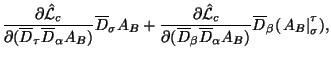
![\begin{displaymath}
\hat n^{\alpha\tau\beta}_\sigma \equiv
{\textstyle{\frac{1}{...
...D_\alpha A_{B})}}
\left.A_{B}\right\vert^\beta_\sigma\right].
\end{displaymath}](https://images.astronet.ru/pubd/2001/09/12/0001170672/img116.gif)