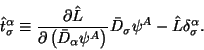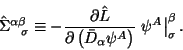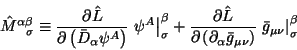- 2.1.1 Problemy opredeleniya uglovogo momenta v polevoi teorii
- 2.1.2 Simmetrizaciya Belinfante
- 2.1.3 Teorema Neter i metod Belinfante
2.1 Klassicheskii metod Belinfante
2.1.1 Problemy opredeleniya uglovogo momenta v polevoi teorii
Vnachale my korotko izlozhim osnovnye polozheniya
original'noi raboty Belinfante [1], vo mnogom dazhe sleduya ego stilyu i
oboznacheniyam. Rassmotrim teoriyu nekotoryh dinamicheskih
polei predstavlennyh obobshennym simvolom ![]() s lagranzhianom
s lagranzhianom
i sohranyaetsya
na vypolnennyh uravneniyah dvizheniya. Sleduya pravilam obychnoi mehaniki tenzornuyu plotnost' uglovogo (orbital'nogo) momenta sledovolo by opredelit' kak
Zdes' voznikaet problema: opredelennyi takim obrazom uglovoi moment ne sohranyaetsya
dazhe s uchetom zakona sohraneniya (2.3). Delo v tom, chto tenzor energii-impul'sa opredelennyi v (2.2) v obshem sluchae ne simmetrichen. Situaciyu v (2.5) mog by spasti sohranyayushiisya simmetrichnyi tenzor energii-impul'sa, kotoryi mozhno bylo by postroit' po drugim pravilam, ili simmetrizovat' uzhe imeyushiisya (2.2).
2.1.2 Simmetrizaciya Belinfante
Vtoruyu iz etih vozmozhnostei ispol'zoval Belinfante [1],
kotoryi predlozhil sleduyushee.
Pust' pri beskonechno malyh vrasheniyah
opredelyaemyh antisimmetrichnym parametrom
![]() variacii koordinat i dinamicheskih peremennyh imeyut vid:
variacii koordinat i dinamicheskih peremennyh imeyut vid:
![]() i
i
![]() ,
gde
,
gde
![]() -- operator.
Opredelim velichinu
-- operator.
Opredelim velichinu
Dalee velichinu (2.6) ili ee obobsheniya my budem nazyvat' popravkoi Belinfante. Teper' dobavim proizvodnuyu ot (2.6) k kanonicheskomu vyrazheniyu (2.2):
Kak i prezhde, v (2.3):
sohranyaetsya
2.1.3 Teorema Neter i metod Belinfante
V original'nom izlozhenii metod Belinfante
predstavlen, faktichesti, na urovne uravnenii dvizheniya.
Seichas my opishem ego edinym obrazom v ramkah
lagranzhevoi teorii.
Dlya etogo zapishem lagranzhian (2.1) v obshekovariantnom vide:
s opredelennoi kak v lekcii 1 proizvodnoi Li:
i proizvol'nym vektorom
Struktura etogo toka vazhna i my ee obsudim podrobno. Pervyi chlen -- eto simmetrichnyi (tak nazyvaemyi metricheskii) tenzor energii-impul'sa polei
vtoroe slagaemoe vyrazheno uzhe izvestnym kanonicheskim tenzorom energii-impul'sa (2.2), tol'ko teper' my zapisyvaem ego v yavno kovariantnom vide:
V tret'em slagaemom v (2.11) glavnuyu rol' igraet spinovyi tenzor:
My predpolagaem, chto uravneniya dvizheniya
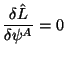 |
vypolnyayutsya i ne budem bol'she uchityvat' predposlednii chlen v (2.11). Nakonec, strukturu Z-chlena my ne vypisyvaem, no otmechaem, chto on ischezaet na killingovyh vektorah fona.
V silu tozhdestva
![]() dolzhen sushestvovat' superpotencial, to est' antisimmetrichnaya
tenzornaya plotnost'. Deistvitel'no, takoi superpotencial sushestvuet,
i zakon sohraneniya
dolzhen sushestvovat' superpotencial, to est' antisimmetrichnaya
tenzornaya plotnost'. Deistvitel'no, takoi superpotencial sushestvuet,
i zakon sohraneniya
![]() mozhet byt' zamenen
zakonom sohraneniya:
mozhet byt' zamenen
zakonom sohraneniya:
antisimmetrichna po verhnim indeksam:
Sravnivaya opredeleniya (2.7) i (2.14)
my opredelyaem popravku
Belinfante tochno takzhe kak v (2.6):
i dobavim k obeim chastyam
V silu opredeleniya (2.17) spinovyi chlen v levoi chasti (2.18) kompensiruetsya dobavkoi Belinfante. Krome togo, okazyvaetsya, chto vyrazheniya v formulah (2.16) i (2.17) sovpadayut v obshem sluchae:
Teper' zapishem simmetrizovannyi s pomosh'yu metoda Belinfante, kak eto bylo sdelano v (2.8), kanonicheskii tenzor energii-impul'sa:
Sravnivaya poslednie dva ravenstva nahodim, chto simmetrizovannyi tenzor energii-impul'sa (2.19) raven metricheskomu tenzoru energii-impul'sa (2.12):
![]() .
.
Elektordinamika,
lagranzhian kotoroi sootvetstvuet forme (2.9),
yavlyaetsya horoshei illyustraciei izlozhennogo. Kanonicheskii tenzor energii- impul'sa (2.13) i tenzor spina (2.14) preobretayut vid:
| = | 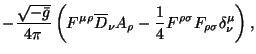 |
||
| = | ![$\displaystyle -{\sqrt{-\bar g}\over 4\pi}F^{\mu[\rho}A^{\sigma]}.$](https://images.astronet.ru/pubd/2001/09/12/0001170672/img197.gif) |
Togda popravka Belinfante (2.17) zapisyvaetsya kak
![$\displaystyle \hat S^{\dag\mu\nu\rho}=
\hat \Sigma^{\dag\rho[\mu\nu]}+
\hat \Si...
...-
\hat \Sigma^{\dag\nu[\rho\mu]}= {\sqrt{-\bar g}\over 4\pi} F^{\mu\nu}A^{\rho}$](https://images.astronet.ru/pubd/2001/09/12/0001170672/img198.gif) |
i privodit k Belinfante modificirovannomu tenzoru energii-impul'sa (2.19):
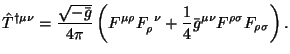 |
S drugoi storony, eto est' izvestnyi simmetrichnyi, kalibrovochno invariantnyi tenzor energii-impul'sa elektoromagnitnogo polya, kotoryi poluchaetsya var'irovaniem
<< 2. Razvitie i obobshenie ... | Oglavlenie | 2.2 Prilozhenie procedury Belinfante ... >>
|
Publikacii s klyuchevymi slovami:
zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |
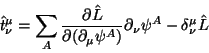
![\begin{displaymath}
\hat f_{\mu\nu}^{ \alpha} \equiv
\sum_A {{\partial \hat L}\...
... {\partial(\partial_\alpha \psi^A)}}{\bf S}_{[\mu\nu]}
\psi^A.
\end{displaymath}](https://images.astronet.ru/pubd/2001/09/12/0001170672/img164.gif)