Astronet > 2.2 Prilozhenie procedury Belinfante k modeli Kaca, Bichaka i Linden-Bella

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

<< 2.1 Klassicheskii metod Belinfante | Oglavlenie | 2.3 Obobshennaya procedura Belinfante ... >>

Razdely

2.2 Prilozhenie procedury Belinfante k modeli Kaca, Bichaka i Linden-Bella

2.2.1 Obosnovanie ispol'zovaniya metoda Belinfante v modeli KBL

Neobhodimost' ispol'zovaniya fona zalozhena v samom opredelenii metoda Belinfante [1]. V teoriyah s lagranzhianom (2.9) vzaimodeistviya rasssmatrivayutsya na zadannom fone, kotoryi yavlyaetsya neobhodimoi sostavlyayushei modeli, i eto privodit k uspehu primeneniya metoda. Simmetrizuya psevdotenzor Einshteina, Papapetrou [3] vynuzhden byl ispol'zovat' vspomogatel'nuyu metriku Minkovskogo. I, deistvitel'no, primenenie etogo metoda v OTO bez ispol'zovaniya fona [4] daet ,,nerazumnye'' nulevye rezul'taty dlya sohranyayushihsya velichin. Mozhno li v OTO, v bolee slozhnyh sluchayah, chem rassmotrel Papapetrou [3], primenyat' etot metod?

Cnova vspomnim o modeli Kaca-Bichaka-Linden-Bella [5] (KBL), kotoraya byla podrobno izlozhena v lekcii 1. S odnoi storony, v model' KBL vklyuchena fonovaya metrika, napomnim, KBL lagranzhian est'

$\begin{displaymath} {\hat{\cal L}}_G = {\hat{\cal L}} - \bar {{\hat{\cal L}}} ... ... \over 2\kappa} \left(\hat R + \partial_\mu \hat k^\mu\right), \end{displaymath}$

(2.20)

gde

$\hat R = \hat g^{\theta\sigma}\left( \overline D_\rho \Delta^\rho_{\theta\sigm... ...a^\eta_{\theta\rho}\right) + \hat g^{\theta\sigma}\overline R_{\theta\sigma},$

$\hat k^\mu = \hat g^{\mu\rho} \Delta^\sigma_{\rho\sigma} - \hat g^{\rho\sigma} \Delta^\mu_{\rho\sigma}$ ,

$\Delta^\alpha_{\mu\nu} \equiv {\textstyle{\frac{1}{2}}} g^{\alpha\beta} \left(\... ...} g_{\mu\nu}\right) = \Gamma^\alpha_{\mu\nu} - \overline \Gamma^\alpha_{\mu\nu}$ .

S drugoi storony, v zakone sohraneniya KBL

$\begin{displaymath} J^\mu(\xi) = \partial_\nu \hat J^{\mu\nu} (\xi) \end{displaymath}$

(2.21)

forma toka standartna:

$\begin{displaymath} \hat J^\mu = \hat \theta^\mu_\nu \xi^\nu + \hat \sigma^{\mu\rho\sigma}\overline D_{[\rho}\xi_{\sigma]}+ \hat Z^\mu(\xi), \end{displaymath}$

(2.22)

s obobshennym tenzorom energii-impul'sa $\hat \theta^\mu_\nu$ i predstavlennym yavno spinovym chlenom $\hat \sigma^{\mu\rho\sigma}$ . Procedura Belinfante kak raz dolzhna preobrazovat' $\hat \theta^\mu_\nu$ tak, chtoby spinovyi chlen ischez iz yavnogo rassmotreniya kak eto proishodit v (2.19). Takim obrazom my imeem horoshie predposylki dlya primeneniya metoda Belinfante k modeli KBL. Voznikaet vopros: A zachem kak-to izmenyat' KBL model', kotoraya obladaet ryadom dostoinstv, udovletvoryaya trebovaniyam (i) - (vii) otmechennym v lekcii 1? Okazyvaetsya, krome dostoinstv, sushestvuyut i problemnye voprosy, kotorye mozhno pred'yavit' k KBL modeli, i kotorye mozhno razreshit' Belinfante metodom.

1. Odin iz nih sostoit v tom, chto nevozmozhno postroit' uglovoi moment izolirovannoi sistemy tol'ko s pomosh'yu 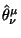$\hat \theta^\mu_\nu$ , neobhodimo privlech' tenzor spina 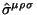$\hat \sigma^{\mu\rho\sigma}$ . Predstavlyaetsya bolee predpochtitel'nym, esli odni i te zhe svoistva modeli opisyvayutsya minimal'nym kolichestvom ob'ektov, a luchshe edinym. Imenno dlya etogo prednaznachen Belinfante metod. Imenno poetomu mnogie avtory 50-h godov, vklyuchaya Landau i Lifshica [6], Goldberga [7], stremilis' postroit' simmetrichnye psevdotenzory. Starayas' izbezhat' ispol'zovaniya spinovogo chlena, Papapetrou [3] primenil metod Belinfante k psevdotenzoru Einshteina.
2. Drugoi vopros sostoit v tom, chto forma kanonicheskih velichin, opredelyaemyh metodom Neter, zavisit ot divergencii, kotorye mogut byt' dobavleny k lagranzhianu. A eto oznachaet, chto dlya raznyh granichnyh uslovii my dolzhny ispol'zovat' kazhdyi raz sovsem razlichnye velichiny. S odnoi storony, v etom net tragedii. V termodinamike tak i proishodit, i avtory rabot [8] 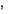$^{\!, }$ [9], appeliruya k takoi analogii nahodyat v etom preimushestvo. S drugoi storony, naprimer, vyrazhenie dlya plotnosti energii vibriruyushei struny ne zavisit ot togo, kak zakrepleny ee koncy, ono vsegda odno i to zhe. Ishodya iz etogo my hoteli by izmenit' tak KBL model', chtoby obshaya forma sohranyayushegosya toka i superpotenciala ne zaviseli ot divergencii v lagranzhiane.

2.2.2 Prilozhenie metoda Belinfante k KBL modeli

V ostatke etoi chasti lekcii 2 izlagayutsya rezul'taty, opublikovannye v rabotah [10] $^{\!- }$ [12]. Itak, dlya spinovyh koefficientov KBL postroim popravku Belinfante po standartnym pravilam (2.17):

$\begin{displaymath} \hat{S}^{\mu\nu\rho}= - \hat{S}^{\nu\mu\rho}=\hat\sigma^{\rho[\mu\nu]}+ \hat\sigma^{\mu[\rho\nu]}-\hat\sigma^{\nu[\rho\mu]}. \end{displaymath}$

(2.23)

Perepishem zakon sohraneniya KBL (2.21) v ekvivalentnoi forme:


		$\displaystyle \hat J^\mu + \partial_\nu\left(\hat{S}^{\mu\nu\rho}\xi_\rho\right) = \partial_\nu\left(\hat J^{\mu\nu}+\hat{S}^{\mu\nu\rho}\xi_\rho\right),$

gde vvedem oboznacheniya dlya novyh toka i superpotenciala, i predstavim strukturu toka:

$\begin{displaymath} \hat {\cal I}^{\mu} = \hat {\cal T}^\mu_\nu\xi^\nu + \hat {\cal Z}^\mu = \partial_\nu\hat {\cal I}^{\mu\nu}. \end{displaymath}$

(2.24)

Zametim, chto spinovyi chlen, kak i polozheno, otsutstvuet. ,,Simmetrizovannyi'' obobshennyi tenzor energii-impul'sa imeet vid:

$\begin{displaymath} \hat {\cal T}^\mu_\nu= \hat \theta^\mu_\nu + \bar D_\rho \hat S^{\mu\rho}_{ \nu}, \end{displaymath}$

(2.25)

a Z-chlen, kak i vezde, obrashaetsya v nul' na killingovyh vektorah fona.

Novyi superpotencial imeet formu:

$\begin{displaymath} \hat {\cal I}^{\mu\nu}= {1 \over \kappa} \hat l^{\rho[\mu}\o... ...\rho\xi^{\nu]} + \hat {\cal P}^{\mu\nu}{_\lambda} \xi^\lambda, \end{displaymath}$

(2.26)

gde $\hat l^{\mu\nu} \equiv \hat g^{\mu\nu} - \overline {\hat g}^{\mu\nu}$ -- vozmushenie metricheskoi plotnosti otnositel'no fonovoi. Superpotengcial (2.26) antisimmetrichen, poskol'ku tenzornaya plotnost' $\hat {\cal P}^{\nu\mu\rho}$ antisimmetrichna po pervym dvum indeksam. Velichina

$\begin{displaymath} \hat {\cal P}^{\mu\nu\rho} = {1 \over 2\kappa} \overline D_\... ...u} \hat l^{\nu\rho}+\bar g^{\sigma\nu} \hat l^{\mu\rho}\right) \end{displaymath}$

(2.27)

interesna i sama po sebe: dlya ${\bar g}^{\mu\nu} = {\eta}^{\mu\nu}$ ona perehodit v izvestnyi superpotencial Papapetrou [3]. Takim obrazom superpotencial (2.26) yavlyaetsya obobsheniem superpotenciala Papapetrou na proizvol'no iskrivlennyi fon i dlya proizvol'nyh vektorov $\xi^\alpha$ .

2.2.3 Svoistva novyh zakonov sohraneniya

V rezul'tate sohraneny vse poleznye svoistva KBL modeli, korotko povtorim ih:

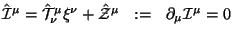(i) Postroen sohranyayushiisya tok: $\hat {\cal I}^\mu = \hat {\cal T}^\mu_\nu\xi^\nu + \hat {\cal Z}^\mu := \partial_\mu {\cal I}^\mu =0$ .
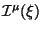(ii) ${\cal I}^\mu(\xi)$ opredelyaetsya Neter-Belinfante proceduroi i dannym lagranzhianom. Sm. obsuzhdenie voprosa edinstvennosti v sleduyushei chasti lekcii 2.
(iii) Sohranena obshaya kovariantnost'.
(iv) Zakony sohraneniya rabotayut na proizvol'no iskrivlennyh fonah.
(v) Ispol'zuyutsya proizvol'nye $\xi^\mu$ .
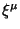(vi) Postroen sootvetstvuyushii antisimmetrichnyi superpotencial.
(vii) Udovletvoryayutsya neobhodimye estestvennye testy.

Krome sohranennyh svoistv poyavilis' novye:

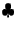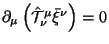$\clubsuit$ (viii) Spinovyi chlen ischez iz opredeleniya toka. Dlya lyubogo fonovogo vektora Killinga (v tom chisle dlya prostranstvennyh vrashenii, esli oni prisutstvuyut) budet ispol'zovat'sya sohranyayushiisya tok, opredelyaemyi TOL'KO obobshennym tenzorom energii-impul'sa: $\partial_\mu \left(\hat {\cal T}^\mu_\nu{\bar\xi}^\nu\right) = 0$ . Sm. takzhe obsuzhdenie dalee.
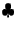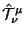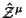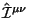$\clubsuit$ (ix) Velichiny $\hat {\cal T}^\mu_\nu$ , $\hat {\cal Z}^\mu$ i $\hat {\cal I}^{\mu\nu}$ ne zavisyat ot divergencii v lagranzhiane. Sm. obsuzhdenie v sleduyushei chasti lekcii 2.
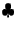$\clubsuit$ (x) Svoistva novogo obobshennogo tenzora energii-impul'sa.
Tenzor energii-impul'sa v (2.24) imeet vid:

$\begin{displaymath} \hat {\cal T}^{\mu\nu} = (\hat T^{(\mu}_\rho\overline g^{\nu... ... {1\over \kappa} {\hat l}^{\lambda[\mu} \bar R^{\nu]}_\lambda. \end{displaymath}$ (2.28)

(a) Kak i v kanonicheskom analoge, pervoe slagaemoe -- eto vozmushenie material'nogo tenzora energii-impul'sa, pravda teper' simmetrizovannoe.
(b) Vtoroi chlen -- eto simmetrichnyi tenzor energii-impul'sa svobodnogo gravitacionnogo polya:

$\displaystyle \kappa \hat \tau^{\mu\nu}$ = $\displaystyle {\textstyle{\frac{1}{2}}} \left(\hat l^{\mu\nu}\overline g^{\rho\... ...u\nu}\hat l^{\rho\sigma}\right) \overline D_\sigma \Delta^\lambda_{\rho\lambda}$

+ $\displaystyle \left(\hat l^{\rho\sigma} \overline g^{\lambda(\mu} - \overline g... ...igma}\hat l^{\lambda(\mu}\right) \overline D_\sigma \Delta^{\nu)}_{\lambda\rho}$

+ $\displaystyle \overline g^{\rho\sigma}\left({\textstyle{\frac{1}{2}}}\hat g^{\m... ...hat g^{\lambda\eta}\Delta^{(\mu}_{\lambda\rho}\Delta^{\nu)}_{\eta\sigma}\right)$

+ $\displaystyle \overline g^{\rho\sigma}\left(\Delta^{\lambda}_{\sigma\eta}\Delta... ...Delta^{\lambda}_{\sigma\lambda}\Delta^{(\mu}_{\eta\rho}\hat g^{\nu)\eta}\right)$

+ $\displaystyle {\textstyle{\frac{1}{2}}} \hat g^{\lambda\eta} \overline g^{\mu\nu}\Delta^\sigma_{\rho\lambda}\Delta^\rho_{\sigma\eta}$

+ $\displaystyle \hat g^{\lambda\eta} \left(\Delta^{\sigma}_{\rho\sigma}\Delta^{(\... ...^{\sigma}_{\lambda\rho}\Delta^{(\mu}_{\eta\sigma}\right)\overline g^{\nu)\rho}.$ (2.29)

(c) Poslednie dva chlena v (2.28) otvechayut za ,,potencial'noe'' vzaimodeistvie s fonovoi geometriei. Pervyi iz nih simmetrichen, vtoroi -- antisimmetrichen. Eto privodit k tomu, chto 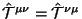$\hat {\cal T}^{\mu\nu}=\hat {\cal T}^{\nu\mu}$ esli i tol'ko esli 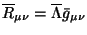$\overline R_{\mu\nu} = \overline \Lambda \bar g_{\mu\nu}$ s postoyannoi 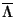$\overline \Lambda$ , to est' esli fonovoe prostranstvo-vremya -- eto prostranstvo Einshteina po Petrovu [13]. Takim obrazom, simmetrizaciya Belinfante pri obobshenii na iskrivlennye fony okazalas' ogranichennoi -- v smysle ,,simmetrizacii'' -- prostranstvami Einshteina.
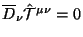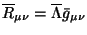(d) V lekcii 1 my opredelilis', chto dlya postroeniya global'nyh zakonov sohraneniya vazhnym yavlyaetsya ,,differencial'noe'' sohranenie toka. Tem ne menee, interesno: vypolnyaetsya li differencial'nyi zakon sohraneniya dlya obobshennogo tenzora energii-impul'sa? 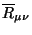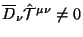Okazyvaetsya, chto $\overline D_\nu \hat {\cal T}^{\mu\nu}= 0$ esli i tol'ko esli $\overline R_{\mu\nu} = \overline \Lambda \bar g_{\mu\nu}$ , dlya bolee slozhnyh $\overline R_{\mu\nu}$ poluchim $\overline D_\nu \hat {\cal T}^{\mu\nu}\neq 0$ .
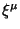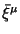(e) Nesmotrya na to, chto v sluchae samogo obshego fona net simmetrizacii tenzora energii-impul'sa i net differencial'nogo zakona sohraneniya dlya tenzora energii-impul'sa, metod Belinfante vyponil svoyu zadachu. Tok sohranyaetsya na vseh proizvol'no iskrivlennyh fonah bez yavnogo uchastiya spinovogo chlena. 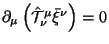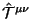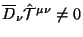V sluchae esli $\xi^\mu$ raven ${\bar\xi}^\mu$ -- vektoru Killinga fona, to etot zakon sohraneniya uproshaetsya do: $\partial_\mu \left(\hat {\cal T}^\mu_\nu{\bar\xi}^\nu\right) = 0$ , gde uchastvuet tol'ko $\hat {\cal T}^{\mu\nu}$ , hotya by i ne simmetrichnyi(!), hotya by i $\overline D_\nu \hat {\cal T}^{\mu\nu}\neq 0$ (!). Eto predstavlyaetsya vazhnym dlya prilozhenii v kosmologicheskih zadachah. 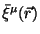Deistvitel'no, resheniya Fridmana ne yavlyayutsya prostranstvami Einshteina, no oni obladayut, naprimer, killingovymi vektorami vrashenii ${\bar\xi}^\mu{(\vec r)}$ . Eto znachit, chto s pomosh'yu 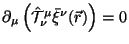$\partial_\mu \left(\hat {\cal T}^\mu_\nu{\bar\xi}^\nu{(\vec r)}\right) = 0$ , mogut byt' raschitany uglovye momenty astrofizicheskih ob'ektov na fone fridmanovskoi geometrii.
(f) Ostalsya vopros o vtoryh proizvodnyh v tenzore energii-impul'sa (2.29). Voobshe govorya, v teorii s uravneniyami vtorogo poryadka ih prisutstvie v tenzore energii-impul'sa nezhelatel'no v smysle postanovki nachal'noi zadachi. Mnogie avtory (sm., naprimer, nedavnyuyu rabotu [14]), predpochitayut imet' tol'ko pervye proizvodnye v tenzore energii-im- pul'sa. No davaite obsudim, tak li plohi nashi dela. Pust' nachal'naya giperpoverhnost' zadaetsya kak x⁰=0. Global'nye velichiny, kak my ih opredelili v lekcii 1, zadayutsya nulevoi komponentoi toka:

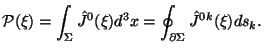
$\displaystyle {\cal P}(\xi) = \int_{\Sigma} \hat J^0(\xi)d^3 x = \oint_{\partial\Sigma} \hat J^{0k}(\xi)ds_k.$

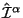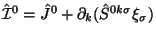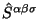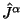Nulevaya komponenta novogo toka $\hat {\cal I}^\alpha$ vyrazhaetsya cherez tok KBL i popravku Belinfante kak $\hat {\cal I}^0= \hat J^0 + \partial_k (\hat S^{0k\sigma}\xi_\sigma)$ ; (k=1, 2, 3). Ostalas' tol'ko prostranstvennaya divergenciya po prichine, chto popravka $\hat S^{\alpha\beta\sigma}$ atisimmetrichna po pervym dvum indeksam. 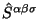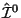No poskol'ku KBL tok $\hat J^\alpha$ i popravka $\hat S^{\alpha\beta\sigma}$ zavisyat tol'ko ot pervyh proizvodnyh, to $\hat {\cal I}^{0}$ soderzhit tol'ko pervye vremennye proizvodnye. Takim obrazom, nachal'naya zadacha mozhet byt' opredelena korrektno.
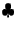$\clubsuit$ (xi) Nakonec, obsudim svoistva novogo superpotenciala (2.26).
(a) Kak my uzhe otmetili, (2.26) antisimmetrichen v silu antisimmetrii velichiny 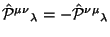$\hat {\cal P}^{\mu\nu}{_\lambda} = -\hat {\cal P}^{\nu\mu}{_\lambda}$ , opredelennoi v (2.27). My takzhe otmetili, chto superpotencial (2.26) obobshaet superpotencial Papapetrou [3].
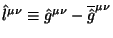(b) Na nash vzglyad kazhetsya vazhnym, chto novyi superpotencil lineino zavisit ot vozmushenii metricheskoi plotnosti: $\hat l^{\mu\nu} \equiv \hat g^{\mu\nu} - \overline {\hat g}^{\mu\nu}$ . 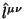Deistvitel'no, model' postroena bez priblizhenii, i v zadachah, gde rassmativayutsya vozmusheniya otnositel'no zadannogo fona my mogli by ne zabotit'sya o probleme shodimosti approksimacii v kazhdom sleduyushem poryadke v zavisimosti ot malosti $\hat l^{\mu\nu}$ , tak kak nashe vyrazhenie dlya superpotenciala tochnoe.
(c) Sushestvuet drugaya poleznaya forma novogo superpotenciala:

$\displaystyle \hat {\cal I}^{\mu\nu}= {1 \over \kappa} \left(\hat l^{\rho[\mu}\... ...igma \hat l^{\nu]\sigma}-\bar D^{[\mu}\hat l^{\nu ]}_\sigma \xi^\sigma \right).$

Po forme etot superpotencial sovpadaet s superpotencialom Abbotta-Dezera [15], odnako oni rashodyatsya nachinaya so vtorogo poryadka vozmushenii, i eto vazhno. Kak bylo otmecheno, nash novyi superpotencial (2.26) udovletvoryaet vsem priznannym estestvennym testam, v to vremya kak superpotencial Abbotta-Dezera ne daet pravil'nogo 4-impul'sa Bondi-Saksa dlya izluchayushei sistemy [12].

<< 2.1 Klassicheskii metod Belinfante | Oglavlenie | 2.3 Obobshennaya procedura Belinfante ... >>

Publikacii s klyuchevymi slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya Publikacii so slovami: zakony sohraneniya - Obshaya teoriya otnositel'nosti - gravitaciya
Sm. takzhe: Padenie shara v Solnechnoi sisteme Gravitacionnye anomalii na Merkurii Galaktika Arp 94 Sputniki GRAIL sostavlyayut kartu lunnoi gravitacii 70 let Stivenu Hokingu Molotok protiv peryshka na Lune Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vse publikacii na tu zhe temu >>

Obsudit' etu publikaciyu

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

$\displaystyle \kappa \hat \tau^{\mu\nu}$	=	$\displaystyle {\textstyle{\frac{1}{2}}} \left(\hat l^{\mu\nu}\overline g^{\rho\... ...u\nu}\hat l^{\rho\sigma}\right) \overline D_\sigma \Delta^\lambda_{\rho\lambda}$
	+	$\displaystyle \left(\hat l^{\rho\sigma} \overline g^{\lambda(\mu} - \overline g... ...igma}\hat l^{\lambda(\mu}\right) \overline D_\sigma \Delta^{\nu)}_{\lambda\rho}$
	+	$\displaystyle \overline g^{\rho\sigma}\left({\textstyle{\frac{1}{2}}}\hat g^{\m... ...hat g^{\lambda\eta}\Delta^{(\mu}_{\lambda\rho}\Delta^{\nu)}_{\eta\sigma}\right)$
	+	$\displaystyle \overline g^{\rho\sigma}\left(\Delta^{\lambda}_{\sigma\eta}\Delta... ...Delta^{\lambda}_{\sigma\lambda}\Delta^{(\mu}_{\eta\rho}\hat g^{\nu)\eta}\right)$
	+	$\displaystyle {\textstyle{\frac{1}{2}}} \hat g^{\lambda\eta} \overline g^{\mu\nu}\Delta^\sigma_{\rho\lambda}\Delta^\rho_{\sigma\eta}$
	+	$\displaystyle \hat g^{\lambda\eta} \left(\Delta^{\sigma}_{\rho\sigma}\Delta^{(\... ...^{\sigma}_{\lambda\rho}\Delta^{(\mu}_{\eta\sigma}\right)\overline g^{\nu)\rho}.$	(2.29)


		$\displaystyle {\cal P}(\xi) = \int_{\Sigma} \hat J^0(\xi)d^3 x = \oint_{\partial\Sigma} \hat J^{0k}(\xi)ds_k.$


		$\displaystyle \hat {\cal I}^{\mu\nu}= {1 \over \kappa} \left(\hat l^{\rho[\mu}\... ...igma \hat l^{\nu]\sigma}-\bar D^{[\mu}\hat l^{\nu ]}_\sigma \xi^\sigma \right).$