Astronet > Footnotes

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Teoriya otnositel'nosti dlya astronomov

... Eilera ^1.1 Tak v matematike nazyvayutsya parametry gruppy vrasheniya, v chest' znamenitogo rossiiskogo uchenogo, chlena imperatorskoi akademii nauk L.Eilera . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
...\space ^1.2 V astroonomii povorot chashe oboznachayut 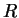, no matematiki predpochitayut grecheskie bukvy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... koordinat ^1.3 Bolee podrobno ob etom mozhno budet prochitat' v knige V.E.Zharova, kotoraya vyhodit v etoi zhe serii . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... ICRF ^1.4 International Celestial Refrence Frame ili mezhdunarodnaya nebesnaya sistema otscheta, v dal'neishem pri ssylkah na etu sistemu budem nazyvayut ee mezhdunarodnoi abbreviaturoi ICRF . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... vida ^2.1 Lineinost' preobrazovanii sleduet iz togo fakta, chto v predele malyh skorostei iskomye preobrazovaniya dolzhny svodit'sya k preobrazovaniyam Galileya i oni dolzhna opisyvat' preobrazovaniya mezhdu dvumya ravnomerno i pryamolineino dvizhushimisya sistemami koordinat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... matrica ^2.2 Kroneker - nemeckii matematik 19 veka, znamenityi svoim izrecheniem "Bog sozdal celye chisla; vse ostal'noe delo ruk cheloveka". Po ironii sud'by byl uchitelem Georga Kantora - nemeckogo matematika, rodivshegosya v Rossii, kotoryi obosnoval sushestvovanie irracional'nyh, transcendentnyh i transfinitnyh chisel v matematike . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... zhizni ^3.1 Podcherkivanie dobavleno pri perevode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... sostoyaniya ^3.2 Konechno v takom rassuzhdenii my prenebregaem soprotivleniem vozduha . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... edinice ^6.1 Rassmotrenie nulevoi geodezicheskoi privodit, razumeetsya k takomu zhe rezul'tatu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... menyayutsya ^6.2 Skalyarnoe pole, razumeetsya mozhet menyat'sya ot tochki k tochke. No komponenta skalyarnogo polya pri parallel'nom perenose iz tochki v tochku ostaetsya neizmennoi. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... vektorom ^6.3 Takie vektora v matematike nazyvayutsya infinitezimal'nymi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... Rimana ^7.1 Riman - znamenityi nemeckii matematik, odin iz treh obshepriznannyh sozdatelei neevklidovoi geometrii. Schitaetsya, chto neevklidovu geometriyu sozdal N.Lobachevskii - matematik, rektor Kazanskogo universiteta. Nezavisimo ot Lobachevskogo geometriyu ne soderzhashuyu postulata o parallel'nyh pryamyh sozdal vengerskii matematik Ya. Boiiyai. K.Riman - tretii v etom spiske, on pervyi issledoval geometriyu polozhitel'noi krivizny. Dvumernyi obraz takoi neevklidovoi geometrii - poverhnost' sfery. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... t.p.^9.1 Eto sleduet iz trebovaniya polozhitel'noi opredelennosti energii. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
... velichina ^9.2 Napomnim, chto integral ot skalyarnoi plotnosti yavlyaetsya skalyarnoi velichinoi. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Publikacii s klyuchevymi slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni Publikacii so slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni
Sm. takzhe: 70 let Stivenu Hokingu Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vsemirnyi god fiziki: triumf Einshteina Al'bert Einshtein opisyvaet prostranstvo-vremya Polnoe solnechnoe zatmenie Otdel pul'sarnoi astrometrii PRAO AKC FIAN O skorosti gravitacii - ot avtorov Vse publikacii na tu zhe temu >>

Mneniya chitatelei [21]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce