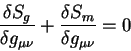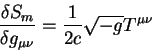Astronet > 9. Uravneniya gravitacionnogo polya

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Teoriya otnositel'nosti dlya astronomov

<< 8. Uravnenie dvizheniya v | Oglavlenie | Rekomenduemaya i citiruemaya literatura >>

Razdely

9. Uravneniya gravitacionnogo polya

Uravnenie gravitacionnogo polya v n'yutonovskoi mehanike horosho izvestno. Gravitacionnaya sila, deistvuyushaya so storony tochechnoi massy

na probnuyu chasticu massy

, raspolozhennuyu na rasstoyanii

ot etogo tela, predstavlyaetsya kak:

$\begin{displaymath} \vec F = -{\displaystyle G m M\over\displaystyle R^3} \vec R \end{displaymath}$

Gravitacionnuyu silu ot proizvol'nogo raspredeleniya mass mozhno poluchit' vzyav integral po plotnosti. Odnako, chashe v teoreticheskoi fizike vvodyat ponyatie gravitacionnogo potenciala $\phi$ , s pomosh'yu kotorogo uzhe vychislyayut gravitacionnuyu silu deistvuyushuyu na probnuyu chasticu:

$\begin{displaymath} F^i = - m_{grav} {\displaystyle\partial \phi\over\displaystyle\partial x^i} \end{displaymath}$

Gravitacionnyi potencial sozdaetsya raspredeleniem mass i uravnenie dlya potenciala imeet vid uravneniya tipa skalyarnogo polya. V otlichie ot sovremennyh uravnenii skalyarnogo polya, uravneniya n'yutonovskogo gravitacionnogo polya ne yavlyayutsya relyativistski invariantnymi, poskol'ku gravitacionnaya teoriya N'yutona sushestvenno nerelyativistskaya teoriya. Poetomu uravneniya polya est' uravnenie tipa Puassona:

$\begin{displaymath} \bigtriangleup \phi = 4 \pi G \rho \end{displaymath}$

(9.1)

Estestvenno, chto n'yutonovskie uravneniya gravitacionnogo polya ne mogli byt' soglasovany s principami relyativistskoi fiziki. Potrebovalos' sozdanie novoi teorii gravitacii - obshei teorii otnositel'nosti.

9.1 Sozdanie uravnenii obshei teorii otnositel'nosti

Posle sozdaniya special'noi teorii otnositel'nosti A.Einshtein nachal razrabotku idei svyazannyh s rasprostraneniem principa otnositel'nosti na uskorennye sistemy otscheta. Dostatochno skoro stalo ponyatno, chto nevozmozhno rasprostranenie principa otnositel'nosti na uskorennye sistemy otscheta bez obsuzhdeniya gravitacionnogo polya.

Pervaya stat'ya [15] otnositsya lish' k odnorodnouskorennym sistemam koordinat. Odnako uzhe tam poyavlyaetsya ideya - otozhdestvlenie uskoreniya i odnorodnogo gravitacionnogo polya. Eta ideya okazalas' ochen' plodotvornoi i reshayushei dlya obobsheniya principa otnositel'nosti - sozdaniya obshei teorii otnositel'nosti, kotoraya vklyuchaet v sebya teoriyu relyativistskogo gravitacionnogo polya. Tam zhe (paragraf 19 etoi stat'i) A.Einshtein poluchaet svyaz' mezhdu tempom techeniya vremeni v gravitacionnom pole s razlichnym potencialom:

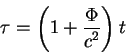
$\begin{displaymath} \tau =\left( 1 + {\displaystyle\Phi\over\displaystyle c^2}\right) t \end{displaymath}$

V sledushem paragrafe A.Einshtein delaet vyvod o tom, chto gravitacionnoe pole nado, po - vidimomu, harakterizovat' peremennoi skorost'yu sveta:

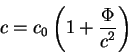
$\begin{displaymath} c=c_0 \left( 1 + {\displaystyle\Phi\over\displaystyle c^2}\right) \end{displaymath}$

Sledushuyu vazhnuyu rabotu, posvyashennuyu gravitacii, A.Einshtein opublikoval tol'ko v 1912 g [16]. V nei on polemiziruet s Abragamom, kotoryi postroil svoyu teoriyu gravitacii i stroit teoriyu gravitacii dlya sluchaya staticheskogo gravitacionnogo polya. V etoi stat'e vse eshe ekspluatiruetsya ideya peremennosti skorosti sveta. A.Einshtein ishet uravnenie dlya sluchaya staticheskogo gravitacionnogo polya, pri etom rukovodstvuetsya uravneniem nerelyativistskogo gravitacionnogo polya. On prihodit k vyvodu, chto uravnenie dolzhno byt' odnorodno po skorosti sveta i privodit ego v vide:

$\begin{displaymath} \Delta c =k c \rho \end{displaymath}$

V sledushei stat'e, opublikovannoi v tom zhe 1912 godu A.Einshtein uchityvaet vklad energii samogo gravitacionnogo polya v gravitacionnoe pole i vpervye poluchaet nelineinoe uravnenie vida:

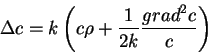
$\begin{displaymath} \Delta c =k \left(c \rho +{\displaystyle 1\over\displaystyle 2k} {\displaystyle grad^2 c\over\displaystyle c}\right) \end{displaymath}$

Uravneniya gravitacionnogo polya stanovyatsya nelineinymi.

V sledushem 1913 g. A.Einshtein v sovmestnoi stat'e s M.Grossmanom [17] yasno formuliruet svyaz' gravitacionnogo polya s metricheskim tenzorom $g_{\mu \nu}$ . Takim obrazom tenzor vtorogo ranga stanovitsya velichinoi, kotoraya opisyvaet gravitacionnoe pole. V etoi zhe stat'e okonchatel'no poyavlyaetsya ideya tozhdestvennosti iskrivlennogo prostranstva - vremeni i gravitacii, poyavlyaetsya tenzor krivizny i drugie velichiny svoistvennye dlya neevklidovoi geometrii. Tam zhe delaetsya popytka vyvesti relyativistskie uravneniya gravitacionnogo polya.

Okonchatel'no relyativistskie uravneniya gravitacionnogo polya byli vyvedeny v 1916 g. V stat'e, opublikovannoi v "Annalah fiziki" [18], A.Einshtein sformuliroval obshuyu teoriyu otnositel'nosti, pridal okonchatel'nyi vid uravneniyam gravitacionnogo polya, kotorymi my pol'zuemsya po sei den' (a takzhe vvel znamenitoe pravilo summirovaniya po povtoryayushimsya indeksam).

Ves'ma skoro posle nachala raboty nad obshei teoriei otnositel'nosti, A.Einshtein ponyal znachenie gamil'tonova podhoda dlya vyvoda uravnenii polya. Etot podhod okazalsya ochen' plodotvornym v sovremennoi teoreticheskoi fizike. On svyazan s ponyatiem ekstremuma deistviya i principom naimen'shego deistviya. Imenno takim obrazom my i budem vyvodit' uravneniya gravitacionnogo polya.

9.1.1 Mozhet li skalyarnoe pole opisyvat' gravitaciyu?

Uravnenie (9.1) yavlyaetsya sushestvenno nerelyativistskim urapvneniem. Eto legko pokazat'. Resheniem uravneniya (9.1) yavlyaetsya integral:

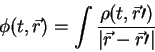
$\begin{displaymath} \phi (t, \vec r) = \int {\displaystyle\rho(t, \vec r \prime)\over\displaystyle\vert\vec r -\vec r \prime\vert} \end{displaymath}$

lyubye izmeneniya v istochnike ( $\rho$ zavisit ot vremeni) mogut byt' mgnovenno obnaruzheny (zdes' my opuskaem problemy svyazannye s obnaruzheniem signala) v tot zhe moment vremeni i na lyubom rasstoyanii ot istochnika. Eto pryamo protivorechit postulatu o nevozmozhnosti peredachi informacii so skorost'yu prevyshayushei skorost' sveta.

Izmenit' eto uravnenie na relyativistskoe kraine prosto. Neobhodimo dobavit' vtoruyu proizvodnuyu po vremeni, prevrativ uravnenie Puassona v uravnenie d'Alambera:

$\begin{displaymath} \Box \phi = 4 \pi G \rho \end{displaymath}$

(9.2)

Sleva v uravnenii teper' stoit relyativistski invariantnyi operator, kotoryi obespechivaet relyativistskuyu invariantnost'. Sprava dolzhen stoyat' istochnik polya (plotnost'), obladayushii takimi zhe svoistvami kak i pole. Esli pole opisyvaetsya skalyarnoi velichinoi, to i istochnik polya takzhe dolzhen byt' skalyarnoi velichinoi. Esli gravitacionnoe pole opisyvaetsya tenzorom ranga , to i istochnik dolzhen byt' tenzorom ranga .

Poskol'ku odnoimennye zaryady v gravitacii prityagivayutsya ( v otlichie ot elektromagnitnoi teorii, v kotoroi odnoimennye zaryady ottalkivayutsya ), to gravitacionnoe pole dolzhno opisyvat'sya tenzorom chetnogo ranga - skalyarnym polem, polem tenzora vtorogo ranga i t.p. ^9.1

Poetomu pri relyativistskom obobshenii n'yutonovskoi teorii gravitacii, opredelyaemoi uravneniem (9.2), neobhodimo opredelit' tenzornye svoistva istochnika polya. Velichina $\rho$ mozhet byt' nerelyativistskim predelom libo tenzora energii - impul'sa $T_{\mu \nu}$ , libo skalyarnoi velichiny - sleda etogo tenzora $T^{\mu}_{\mu}$ . V pervom sluchae gravitacionnoe pole predstavlyaetsya tenzorom vtorogo ranga, vo vtorom sluchae - tenzorom pervogo ranga. Eksperiment pokazyvaet, chto spravedliva teoriya gravitacii s polem vtorogo ranga v kachestve polevoi peremennoi.

9.2 Vyvod uravnenii polya iz variacionnogo principa

9.2.1 Deistvie dlya gravitacionnogo polya

Itak my dolzhny naiti svyaz' mezhdu metricheskim tenzorom $g_{\mu \nu}$ i raspredeleniem mass, kotoraya zamenit uravnenie (9.1) klassicheskoi n'yutonovskoi teorii tyagoteniya. Rassmotrim vyvod uravnenii gravitacionnogo polya v obshei teorii otnositel'nosti ( uravnenii Einshteina ) ispol'zuya princip naimen'shego deistviya. Uravneniya gravitacionnogo polya poluchatsya variaciei deistviya po metricheskomu tenzoru - polevoi peremennoi. Eto deistvie, kak i dlya polei drugogo vida dolzhno byt' predstavleno v vide nekotorogo skalyara, kotoryi yavlyaetsya integralom po 4 prostranstvu ot nekotoroi skalyarnoi plotnosti, zavisyashei ot metricheskogo tenzora i pervyh proizvodnyh metricheskogo tenzora. Takoi skalyarnoi plotnost'yu yavlyaetsya tol'ko velichina:

$\begin{displaymath} \sqrt{-g} R \end{displaymath}$

obrazuemaya iz skalyara krivizny. Deistvie gravitacionnogo polya mozhno, sledovatel'no, predstavit' v vide:

$\begin{displaymath} S_g= - \kappa \int R \sqrt{-g} \; d^4 x \end{displaymath}$

(9.3)

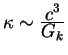Zdes' $\kappa$ -nekotoraya novaya gravitacionnaya postoyannaya. Opredelit' ee svyaz' s kavendishevoi gravitacionnoi postoyannoi s tochnost'yu do bezrazmernogo postoyannogo mnozhitelya dostatochno prosto - deistvie imeet razmernost' energii, skalyar krivizny imeet razmernost' sm $^{-2}$ , a ob'em pri integrirovanii sm. Otsyuda iz soobrazhenii razmernosti nahodim, chto $\kappa \sim {\displaystyle c^3\over\displaystyle G_k}$ , gde - gravitacionnaya postoyannaya Kavendisha.

Skalyarnaya krivizna naryadu s metricheskim tenzorom i ego pervymi proizvodnymi soderzhit takzhe i vtorye proizvodnye ot metricheskogo tenzora. Primenyaya k $\sqrt{-g} R$ proizvodnuyu Eilera - Lagranzha mozhno poluchit' uravneiya gravitacionnogo polya. Pryamye vychisleniya ochen' trudoemkie i soderzhat bol'shoe kolichestvo vykladok. My neskol'ko uprostim vychisleniya, dlya chego vospol'zuemsya dvumya svoistvami skalyara krivizny.

Pervyi priem pri vyvode uravnenii gravitacionnogo polya vpervye primenili [8]. On osnovan na tom, chto v skalyarnoi krivizne vtorye proizvodnye metricheskogo tenzora vhodyat lineino, chto pozvolyaet vydelit' polnuyu divergenciyu, kotoraya ne vliyaet na uravneniya dvizheniya. Poetomu deistvie mozhno predstavit' v vide:

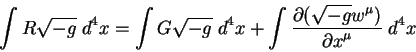
$\begin{displaymath} \int R \sqrt{-g} \; d^4 x = \int G \sqrt{-g} \; d^4 x + \int... ...sqrt{-g} w^{\mu})\over\displaystyle\partial x^{\mu}} \; d^4 x \end{displaymath}$

Sleva stoit skalyarnaya velichina^9.2. Sprava stoyat dva neinvariantnyh chlena. Hotya ih summa yavlyaetsya invariantom, kazhdyi iz chlenov neinvarianten. Dlya vyvoda uravnenii polya narushenie invariantnosti ne strashno, poskol'ku pri vyvode ispol'zuyutsya variacii etih velichin. Napomnim, chto variacii mnogih neinvariantnyh velichin yavlyayutsya uzhe invariantnymi, primer, simvol Kristoffelya ne yavlyayutsya tenzorom, v to vremya kak variacii simvola uzhe yavlyayutsya tenzorom tret'ego ranga.

Krome togo, polnuyu divergenciyu po teoreme Ostragradskogo mozhno preobrazovat' v integral po trehmernoi giperpoverhnosti. Pri vychislenii variacii etot chlen budet raven nulyu, tak kak po opredeleniyu variacii na giperpoverhnosti, ohvatyvayushei ob'em ravny nulyu. Poetomu variaciya gravitacionnogo deistviya ravna:

$\begin{displaymath} \delta S_g = -\kappa \delta \int G \sqrt{-g} \; d^4 x \end{displaymath}$

Naidem velichinu , kotoraya opredelyaet deistvie gravitacionnogo polya i vychislim ee variaciyu otnositel'no metricheskogo tenzora.

Skalyarnaya plotnost' krivizny vyrazhaetsya cherez metricheskii tenzor i simvoly Kristoffelya kak:

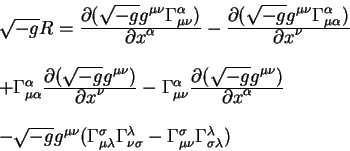
$\begin{displaymath} \begin{array}{l} \sqrt{-g} R = {\displaystyle\partial (\sqrt... ..._{\mu \nu} \Gamma^{\lambda}_{\sigma \lambda}\bigr) \end{array}\end{displaymath}$

Nahodim velichiny

$\begin{displaymath} w^{\alpha} = g^{\mu \nu} \Gamma^{\alpha}_{\mu \nu} - g^{\mu \alpha} \Gamma^{\nu}_{\mu \nu} \end{displaymath}$

$\begin{displaymath} G=g^{\mu \nu}\bigl( \Gamma^{\sigma}_{\mu \lambda} \Gamma^{\... ...ma^{\sigma}_{\mu \nu} \Gamma^{\lambda}_{\sigma \lambda}\bigr) \end{displaymath}$

Proizvodnaya Eilera - Lagranzha velichiny $\sqrt{-g}G$ opredelyaet uravneniya gravitacionnogo polya.

9.2.2 Proizvodnaya Eilera - Lagranzha ot deistviya i uravneniya gravitacionnogo polya v vakuume

Proizvodnaya Eilera - Lagranzha ot velichiny $\sqrt{-g}G$ opredelyaetsya kak:

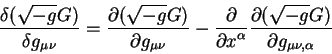
$\begin{displaymath} {\displaystyle\delta (\sqrt{-g}G)\over\displaystyle\delta g_... ... (\sqrt{-g}G)\over\displaystyle\partial g_{\mu \nu, \alpha}} \end{displaymath}$

Kak vidno iz opredeleniya, $\sqrt{-g}G$ zavisit ot samogo metricheskogo tenzora $g_{\mu \nu}$ i simvolov Kristoffelya. Vychislim chastnye proizvodnye ot $g^{\mu \nu}$ i $\sqrt{-g}$ po metricheskomu tenzoru $g_{\mu \nu}$ .

Dlya vychisleniya chastnyh proizvodnyh ot kontravariantnogo metricheskogo tenzora $g^{\mu \nu}$ po kovariantnomu metricheskomu tenzoru $g_{\mu \nu}$ vospol'zuemsya ravenstvom vida:

$\begin{displaymath} g^{\alpha \gamma} g_{\gamma \beta} = \delta^{\alpha}_{\beta} \end{displaymath}$

berya chastnuyu proizvodnuyu po kovariantnomu metricheskomu tenzoru po chastyam poluchaem uravnenie vida:

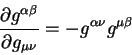
$\begin{displaymath} {\displaystyle\partial g^{\alpha \beta}\over\displaystyle\partial g_{\mu \nu}} = -g^{\alpha \nu} g^{\mu \beta} \end{displaymath}$

v etom uravnenii dostatochno trudno usmotret' simmetriyu po pare indeksov $\alpha \beta$ i $\mu \nu$ . Dlya togo, chtoby sdelat' etu simmetriyu yavnoi, obrazuem simmetrichnuyu summu v pravoi chasti etogo ravenstva, togda chastnaya proizvodnaya budet ravna:

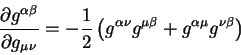
$\begin{displaymath} {\displaystyle\partial g^{\alpha \beta}\over\displaystyle\pa... ...alpha \nu} g^{\mu \beta} +g^{\alpha \mu} g^{\nu \beta} \right) \end{displaymath}$

Dlya vychisleniya chastnoi proizvodnoi ot kornya iz determinanta $\sqrt{-g}$ vospol'zuemsya ravenstvom:

$\begin{displaymath} d(-g) = (-g) g^{\mu \nu} dg_{\mu \nu} \end{displaymath}$

togda poluchaem

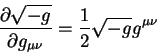
$\begin{displaymath} {\displaystyle\partial \sqrt{-g}\over\displaystyle\partial g_{\mu \nu}} = {1 \over 2} \sqrt{-g} g^{\mu \nu} \end{displaymath}$

Chastnye proizvodnye ot plotnosti deistviya $\sqrt{-g}G$ po kovariantnomu metricheskomu tenzoru $g_{\mu \nu}$ formiruyutsya tol'ko iz chastnyh proizvodnyh ot kontravaiantnyh komponent metricheskogo tenzora $g^{\mu \nu}$ , kotorye vhodyat v simvoly Kristoffelya i v opredelitel' $\sqrt{-g}$ . Proizvodnye ot simvola Kristoffelya est':

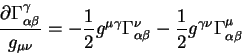
$\begin{displaymath} {\displaystyle\partial \Gamma^{\gamma}_{\alpha \beta}\over\d... ... \beta} -{1 \over 2}g^{\gamma \nu} \Gamma^{\mu}_{\alpha \beta} \end{displaymath}$

Vypishem teper' chastnuyu proizvodnuyu ot plotnosti gravitacionnogo deistviya $\sqrt{-g}G$ po metricheskomu tenzoru:

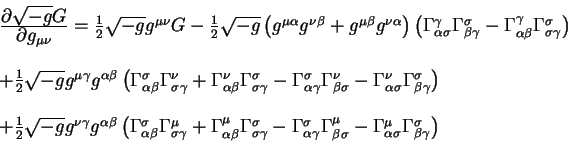
$\begin{displaymath} \begin{array}{l} {\displaystyle\partial \sqrt{-g}G\over\disp... ...a \sigma} \Gamma^{\sigma}_{\beta \gamma} \right) \end{array} \end{displaymath}$

Nesmotrya na gromozdkii vid struktura etoi formuly dostatochna prostaya.

Bolee slozhnoi yavlyaetsya struktura chastnoi proizvodnoi ot gravitacionnogo deistviya po proizvodnoi ot metricheskogo tenzora. Rassmotrim teper' ee.

Rassmotrim kak proishodit differencirovanie funkcii $\sqrt{-g}G$ po proizvodnoi metricheskogo tenzora, skazhem, $g_{i k , l}$ . Poskol'ku proizvodnye ot metricheskogo tenzora po koordinatam soderzhatsya tol'ko v simvolah Kristoffelya $\Gamma^{\alpha}_{\mu \nu}$ , to i chastnaya proizvodnaya budet deistvovat' tol'ko na eti chleny. Tol'ko dlya etih vychislenii budem ispol'zovat' latinskie indeksy v oboznacheniyah metricheskogo tenzora. Tol'ko v etom paragrafe budem schitat', chto oni probegayut znacheniya 0, 1, 2, 3.

Vypishem chastnuyu proizvodnuyu ot simvolov Kristoffelya po nashei dinamicheskoi peremennoi - chastnoi proizvodnoi ot metricheskogo tenzora po odnoi iz koordinat:

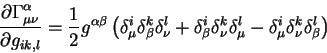
$\begin{displaymath} {\displaystyle\partial \Gamma^{\alpha}_{\mu \nu}\over\displa... ...mu} - \delta^i_{\mu} \delta^k_{\nu} \delta^l_{\beta} \right) \end{displaymath}$

Podstavim etu formulu v vyrazhenie dlya chastnoi proizvodnoi ot plotnosti gravitacionnogo deistviya po nashei dinamicheskoi peremennoi - chastnoi proizvodnoi ot metricheskogo tenzora po odnoi iz koordinat

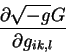
$\begin{displaymath} {\displaystyle\partial \sqrt{-g} G\over\displaystyle\partial g_{ik,l}} \end{displaymath}$

poluchim nekotoroe gromozdkoe vyrazhenie. Ne vypisyvaya ego zdes' celikom, svernem po mertvym indeksam summirovaniya, chto znachitel'no uprostit zapis':

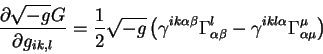
$\begin{displaymath} {\displaystyle\partial \sqrt{-g} G\over\displaystyle\partial... ...a} - \gamma^{ikl \alpha } \Gamma^{\mu}_{\alpha \mu} \right) \end{displaymath}$

V etom uravnenii vveden novyi tenzor chetvertogo ranga

$\begin{displaymath} \gamma^{ik \alpha \beta} =\left( g^{i \alpha} g^{k \beta} + g^{i \beta} g^{k \alpha} - g^{\alpha \beta} g^{ik} \right) \end{displaymath}$

V proizvodnuyu Eilera - Lagranzha chlen vida

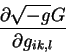
$\begin{displaymath} {\displaystyle\partial \sqrt{-g} G\over\displaystyle\partial g_{ik,l}} \end{displaymath}$

vhodit ne samostoyatel'no, v ot nego vychislyaetsya chastnaya proizvodnaya po koordinate, kotoraya stoit v dinamicheskoi peremennoi - chastnoi proizvodnoi ot metricheskogo tenzora po koordinate

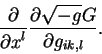
$\begin{displaymath} {\displaystyle\partial\over\displaystyle\partial x^l} {\disp... ...tyle\partial \sqrt{-g} G\over\displaystyle\partial g_{ik,l}}. \end{displaymath}$

Posle vychisleniya chastnyh proizvodnyh po koordinate poyavlyayutsya proizvodnye ot simvolov Kristoffelya po koordinatam:

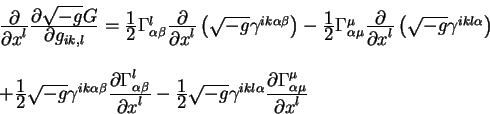
$\begin{displaymath} \begin{array}{l} {\displaystyle\partial\over\displaystyle\pa... ...\mu}_{\alpha \mu}\over\displaystyle\partial x^l} \end{array} \end{displaymath}$

Chastnye proizvodnye ot simvolov Kristoffelya vhodyat v tenzor krivizny. Etot tenzor imeet rang 4. No proizvodnye, kotorye poyavlis' v privedennoi vyshe formule vhodyat v tenzor Richchi. Zapishem etu formulu cherez tenzor Richchi $R_{\alpha \beta}$ .

Vyrazhaya chastnye proizvodnye ot simvolov Kristoffelya cherez tenzor Richchi poluchim chlen v levoi chasti ravenstva vida:

$\begin{displaymath} {\displaystyle 1\over\displaystyle 2} \sqrt{-g} \gamma^{i k \alpha \beta} R_{\alpha \beta} \end{displaymath}$

Vyrazhaya tenzor $\gamma^{i k \alpha \beta}$ v vide proizvedenii metricheskogo tenzora i svertyvaya po indeksam summirovaniya poluchaem chlen vida:

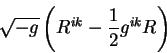
$\begin{displaymath} \sqrt{-g} \left( R^{i k} - {\displaystyle 1\over\displaystyle 2} g^{i k} R \right) \end{displaymath}$

Ostavshiesya chetyre chlena predstavlyayut proizvedeniya simvolov Kristoffelya, okonchatel'no vypishem proizvodnuyu ot gravitacionnogo deistviya v vide:

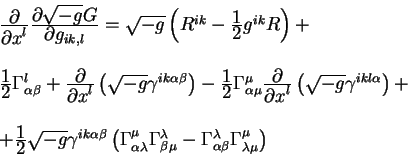
$\begin{displaymath} \begin{array}{l} {\displaystyle\partial\over\displaystyle\pa... ...\alpha \beta} \Gamma^{\mu}_{\lambda \mu} \right) \end{array} \end{displaymath}$

Vypishem okonchatel'no proizvodnuyu Eilera - Lagranzha ot plotnosti gravitacionnogo deistviya:

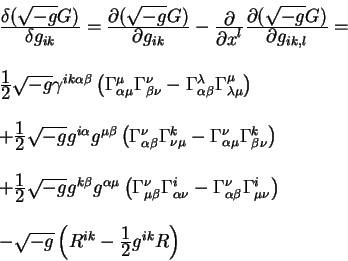
$\begin{displaymath} \begin{array}{l} {\displaystyle\delta (\sqrt{-g} G)\over\dis... ...playstyle 1\over\displaystyle 2} g^{i k} R \right) \end{array}\end{displaymath}$

Dlya uprosheniya dal'neishih vykladok vyberem sistemu koordinat, v kotoroi udovletvoryaetsya uslovie $\sqrt{-g}=1$ vo vsem prostranstve - vremeni. Poskol'ku eto tol'ko odno uslovie, to ego mozhno udovletvorit' podhodyashim vyborom sistemy koordinat vsegda. Dokazatel'stvo etogo utverzhdeniya ne vhodit v nash kurs. Sledstviem etogo vybora yavlyaetsya uravnenie:

$\begin{displaymath} \Gamma^{\mu}_{\alpha \mu} =0 \end{displaymath}$

spravedlivoe dlya lyubogo znacheniya indeksa $\alpha$ . Togda pervyi chlen v etom uravnenii obrashaetsya v nul'.

Podstavim uravnenie dlya proizvodnoi Eilera - Lagranzha v variaciyu deistviya:

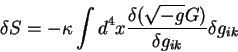
$\begin{displaymath} \delta S= -\kappa \int d^4 x {\displaystyle\delta (\sqrt{-g}G)\over\displaystyle\delta g_{ik}} \delta g_{ik} \end{displaymath}$

Svertka vtorogo i tret'ego chlenov s variaciei metricheskogo tenzora $\delta g_{ik}$ daet nul', poskol'ku eto summa vtorogo i tret'ego chlenov antisimmetrichna po indeksam $i\; k$ . V rezul'tate variaciya gravitacionnogo deistviya po metricheskomu tenzoru ravna:

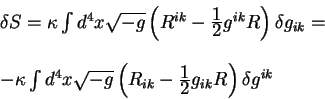
$\begin{displaymath} \begin{array}{l} \delta S= \kappa \int d^4 x \sqrt{-g} \left... ...er\displaystyle 2} g_{i k} R \right) \delta g^{ik} \end{array}\end{displaymath}$

Zametim, chto znak minus v poslednem ravenstve poyavlyaetsya, poskol'ku variacii kontravariantnyh komponent metricheskogo tenzora protivopolozhna variaciyam kovariantnyh komponent:

$\begin{displaymath} \delta g^{\alpha \beta} = -{1 \over 2} \left( g^{i \alpha} g^{k \beta} +g^{k \alpha} g^{i \beta} \right) \delta g_{i k} \end{displaymath}$

Iz variacii deistviya gravitacionnogo polya srazu mozhno poluchit' relyativistskie uravneniya polya v pustom prostranstve:

$\begin{displaymath} R_{\alpha \beta} - {\displaystyle 1\over\displaystyle 2} g_{\alpha \beta} R =0 \end{displaymath}$

(9.4)

Eto uravnenie ekvivalentno uravneniyu:

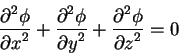
$\begin{displaymath} {\displaystyle\partial^2 \phi\over\displaystyle\partial x^2}... ...isplaystyle\partial^2 \phi\over\displaystyle\partial z^2} = 0 \end{displaymath}$

v n'yutonovskoi teorii gravitacionnogo polya.

Variaciya gravitacionnogo deistviya vychislena v opredelennoi sisteme koordinat, kotoraya udovletvoryaet usloviyu $\sqrt{-g}=1$ . Odnako, uravneniya gravitacionnogo polya polucheny v obshekovariantnom vide, kotoryi spravedliv nezavisimo ot vybora sistemy koordinat.

Dlya vyvoda relyativistskih uravnenii, kotorye svyazyvayut gravitacionnoe pole i raspredelenie materii neobhodimo naiti velichinu, kotoraya poluchaetsya pri variacii plotnosti deistviya ot materii po metricheskomu tenzoru.

9.2.3 Vyvod uravnenii gravitacionnogo polya metodom Pallatini

Prezhde chem pereiti v vyvodu uravnenii obshei teorii otnositel'nosti, kotorye svyazyvayut raspredelenie gravitacionnogo polya (metricheskogo tenzora) s raspredeleniem materii privedem eshe odin vyvod variacii deistviya gravitacionnogo polya, kotoryi yavlyaetsya obshekovariantnym i ne trebuet privlecheniya special'noi sistemy koordinat. Pri etom, vyvod uravnenii relyativistskoi gravitacii metodom Pallatini yavlyaetsya ekonomnym s tochki zreniya vykladok.

Uzhe v predydushem paragrafe chitatel' mog obratit' vnimanie na to, chto vyvod uravnenii gravitacionnogo polya byl otyagoshen mnogimi predpolozheniyami, v chastnosti o vybore special'noi sistemy koordinat. Eto - neobhodimoe sledstvie obshei kovariantnosti teorii. Esli v teorii, naprimer, elektromagnitnogo polya, vychislenie amplitud potenciala i ih proizvodnyh po vremeni i koordinatam dostatochno, chtoby polnost'yu opredelit' evolyuciyu polya, to v obshei teorii otnositel'nosti izmenit' znacheniya metricheskogo tenzora i ego proizvodnyh mozhno s pomosh'yu koordinatnogo preobrazovaniya. Koordinatnoe preobrazovanie metricheskogo tenzora ne neset nikakoi fizicheskoi nagruzki, ono celikom zavisit ot soobrazhenii udobstva vychislenii. Poetomu neobhodimo vydelit' tu chast' v metricheskom tenzore, kotoraya obuslavlivaet dinamicheskuyu evolyuciyu.

Eta problema voznikla potomu, chto v metricheskim tenzore soderzhatsya dopolnitel'nye stepeni svobody dlya togo, chtoby obespechit' pravil'noe povedenie ego komponent pri koordinatnyh preobrazovaniyah. Dopolnitel'nye stepeni svobody podchinyayutsya nekotorym svyazyam, kotorye neobhodimo uchityvat' pri vyvode uravnenii polya.

V sovremennoi teorii polya razrabotan metod, kotoryi pozvolyaet otdelit' dinamicheskuyu chast' ot chasti ne nesushei fizicheskoi informacii [20]. Etot formalizm v sovremennoi teorii polya nazyvaetsya kanonicheskim. U nego est' dva sushestvennyh svoistva. Pervoe zaklyuchaetsya v tom, chto uravneniya polya imeyut pervyi poryadok otnositel'no proizvodnyh po vremeni. Vtoroe svoistvo zaklyuchaetsya v yavnov vydelenii vremeni v lorenc - invariantnoi teorii (tak nazyvaemoe 3+1 rassheplenie). V klassicheskoi mehanike etot formalizm sovpadaet s formalizmom Gamil'tona.

Dlya polucheniya etogo formalizma v obshei teorii otnositel'nosti neobhodimo zapisat' plotnost' deistviya v lineinom otnositel'no pervyh proizvodnyh vide (etot vid nazyvaetsya zapis'yu v forme Pallatini). Obychnyi integral deistviya:

$\begin{displaymath} S=-\kappa \int d^4 x \sqrt{-g} R \end{displaymath}$

daet uravneniya obshei teorii otnositel'nosti pri var'irovanii metricheskogo tenzora $g_{\mu \nu}$ . Poluchivshiesya uravneniya Eilera yavlyayutsya differencial'nymi uravneniyami v chastnyh proizvodnyh vtorogo poryadka otnositel'no metricheskogo tenzora. Odnako, te zhe uravneniya mozhno privesti k kanonicheskomu gamil'tonovu vidu:

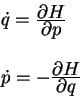
$\begin{displaymath} \begin{array}{l} \dot q ={\displaystyle\partial H\over\displ... ...isplaystyle\partial H\over\displaystyle\partial q} \end{array}\end{displaymath}$

Dlya etogo predstavim plotnost' lagranzhiana gravitacionnogo polya v forme Palatini, pri etom simvoly Kristoffelya rassmatrivayutsya kak nezavisimye peremennye:

$\begin{displaymath} S=-\kappa \int d^4 x \sqrt{-g} g^{\mu \nu} R_{\mu \nu}(\Gamma) \end{displaymath}$

(9.5)

gde

$\begin{displaymath} R_{\mu \nu}(\Gamma) \equiv {\displaystyle\partial \Gamma^{\a... ...ta} - \Gamma^{\alpha}_{\mu \beta} \Gamma^{\beta}_{\alpha \nu} \end{displaymath}$

Zdes' sleduet otmetit', chto kovariantnye komponenty tenzora Richchi ne soderzhat metricheskogo tenzora, a soderzhat tol'ko binarnye proizvedeniya simvolov Kristoffelya i ih proizvodnyh po koordinatam. Var'iruya (9.5) po metricheskomu tenzoru poluchaem uravneniya Einshteina:

$\begin{displaymath} {\displaystyle\delta S\over\displaystyle\delta g^{\mu \nu}} ... ...\displaystyle 1\over\displaystyle 2} g_{\mu \nu} R \right) = 0 \end{displaymath}$

(9.6)

Dopolnitel'no k etim uravneniyam poluchaem uravneniya svyazi, kotorye ustanavlivayut sootnosheniya mezhdu nezavisimymi velichinami $g_{\mu \nu}$ i $\Gamma^{\alpha}_{\mu \nu}$ :

$\begin{displaymath} {\displaystyle\partial \sqrt{-g} g^{\mu \nu}\over\displaysty... ...ha} - \sqrt{-g} g^{\mu \nu} \Gamma^{\beta}_{\beta \alpha} = 0 \end{displaymath}$

reshaya eti uravneniya otnositel'no velichin $\Gamma^{\alpha}_{\mu \nu}$ poluchaem obychnuyu zavisimost' mezhdu simvolami Kristoffelya i metricheskim tenzorom:

$\begin{displaymath} \Gamma^{\alpha}_{\mu \nu} = {\displaystyle 1\over\displaysty... ...eta, \alpha} + g_{\nu \beta, \mu} - g_{\mu \nu, \beta} \right) \end{displaymath}$

9.3 Istochnik gravitacionnogo polya

V predydushem paragrafe polucheny uravneniya obshei teorii otnositel'nosti v vakuume. Polnye uravneniya dolzhny soderzhat' takzhe vliyanie materii na gravitacionnoe pole. Oni dolzhny soderzhat' istochnik gravitacionnogo polya. Polnoe deistvie dlya sistemy gravitacionnoe pole + materiya predstavlyaet iz sebya summu dvuh chlenov: deistviya dlya gravitacionnogo polya i deistvie dlya materii . Polnye uravneniya polya poluchayutsya kak summa variacii deistviya dlya polya i deistviya dlya materii:

$\begin{displaymath} \delta S_g + \delta S_m =0 \end{displaymath}$

Variacii proizvodyatsya po metricheskomu tenzoru, a sami uravneniya poluchayutsya iz priravnivaniem k nulyu pervyh proizvodnyh Eilera - Lagranzha ot deistviya po metricheskomu tenzoru:

$\begin{displaymath} {\displaystyle\delta S_g\over\displaystyle\delta g_{\mu \nu}... ...playstyle\delta S_m\over\displaystyle\delta g_{\mu \nu}} = 0 \end{displaymath}$

(9.7)

Variaciya ot deistviya gravitacionnogo polya po metricheskomu tenzoru est' (9.6):

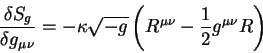
$\begin{displaymath} {\displaystyle\delta S_g\over\displaystyle\delta g_{\mu \nu}... ...- {\displaystyle 1\over\displaystyle 2} g^{\mu \nu} R \right) \end{displaymath}$

Variacii ot po metricheskomu tenzoru nazyvayutsya tenzorom energii - impul'sa:

$\begin{displaymath} {\displaystyle\delta S_m\over\displaystyle\delta g_{\mu \nu}... ...\displaystyle 1\over\displaystyle 2 c} \sqrt{-g} T^{\mu \nu} \end{displaymath}$

(9.8)

Okonchatel'no, uravneniya gravitacionnogo polya v obshei teorii otnositel'nosti imeyut vid:

$\begin{displaymath} R_{\mu \nu} - {\displaystyle 1\over\displaystyle 2} g_{\mu \nu} R ={\displaystyle 8 \pi G\over\displaystyle c^4} T_{\mu \nu} \end{displaymath}$

(9.9)

Zdes' postoyannuyu $1\over\displaystyle 2 c \kappa$ opredelyayut iz togo usloviya, chtoby v predele slabyh polei i medlennyh dvizhenii uravneniya obshei teorii otnositel'nosti sovpadali s uravneniyami N'yutona dlya gravitacionnogo polya.

Privedem neskol'ko primerov tenzora energii - impul'sa.

Tenzor energii - impul'sa svobodnoi chasticy est':

$\begin{displaymath} T_{\mu \nu} = \rho c^2 u_{\mu} u_{\nu} \end{displaymath}$

(9.10)

Tenzor energii - impul'sa ideal'noi zhidkosti est':

$\begin{displaymath} T_{\mu \nu} = (\rho c^2 + p) u_{\mu} u_{\nu} - g_{\mu \nu} p \end{displaymath}$

(9.11)

Zdes' $\rho$ - plotnost' chasticy v pervom primere i plotnost' zhidkosti vo vtorom primere, - davlenie v zhidkosti vo vtorom primere.

<< 8. Uravnenie dvizheniya v | Oglavlenie | Rekomenduemaya i citiruemaya literatura >>

Publikacii s klyuchevymi slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni Publikacii so slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni
Sm. takzhe: 70 let Stivenu Hokingu Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vsemirnyi god fiziki: triumf Einshteina Al'bert Einshtein opisyvaet prostranstvo-vremya Polnoe solnechnoe zatmenie Otdel pul'sarnoi astrometrii PRAO AKC FIAN O skorosti gravitacii - ot avtorov Vse publikacii na tu zhe temu >>

Mneniya chitatelei [21]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce