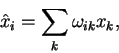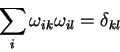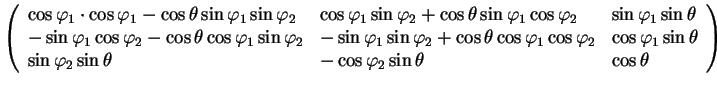<< Vvedenie | Oglavlenie | 2. Special'naya teoriya otnositel'nosti >>
- 1.1 Princip otnositel'nosti Galileya
- 1.2 Trudnosti klassicheskoi mehaniki pri opisanii rasprostraneniya sveta
- 1.3 Special'naya teoriya otnositel'nosti
1. Principy otnositel'nosti
1.1 Princip otnositel'nosti Galileya
Pervyi princip otnositel'nosti (PO) byl sformulirovan eshe v epohu Vozrozhdeniya G.Galileem. PO otnosilsya k mehanike i glasil: "Zakony mehaniki v sisteme koordinat, dvizhusheisya ravnomerno i pryamolineino v prostranstve, imeyut tot zhe vid, chto i v sisteme koordinat, pokoyasheisya v prostranstve".
Iz etogo postulata mozhno sdelat' prostoi vyvod, a imenno: sushestvuet beskonechno mnogo ekvivalentnyh sistem koordinat, nazyvaemyh inercial'nymi i sovershayushimi ravnomernoe i pryamolineinoe dvizhenie ili pokoyashihsya drug otnositel'no druga. V etih sistemah zakony mehaniki vypolnyayutsya v prostoi klassicheskoi forme.
Opredelim srazu, chto zakonami mehaniki zdes' budem nazyvat' zakony dvizheniya v klassicheskoi mehanike i zakony sohraneniya.
Princip otnositel'nosti Galileya na matematicheskim yazyke preobrazovaniya
koordinat obychno formuliruetsya sledushim obrazom. Pust' polozhenie probnoi
chasticy opisyvaetsya v dekartovoi sisteme koordinat
![]() , krome treh prostranstvennyh koordinat my dobavili vremennuyu
koordinatu, kotoraya neobhodima v special'noi teorii otnositel'nosti
(STO) i obshei teorii otnositel'nosti (OTO),
, krome treh prostranstvennyh koordinat my dobavili vremennuyu
koordinatu, kotoraya neobhodima v special'noi teorii otnositel'nosti
(STO) i obshei teorii otnositel'nosti (OTO), ![]() . V sisteme koordinat
. V sisteme koordinat
![]() =
= ![]() ,
, ![]() ,
, ![]() ,
, ![]() , zakony mehaniki
ostayutsya neizmennymi, esli sistema
, zakony mehaniki
ostayutsya neizmennymi, esli sistema ![]() dvizhetsya otnositel'no
sistemy koordinat
dvizhetsya otnositel'no
sistemy koordinat ![]() so skorost'yu
so skorost'yu ![]() , tak, chto dve sistemy koordinat
svyazany mezhdu soboi preobrazovaniem Galileya:
, tak, chto dve sistemy koordinat
svyazany mezhdu soboi preobrazovaniem Galileya:
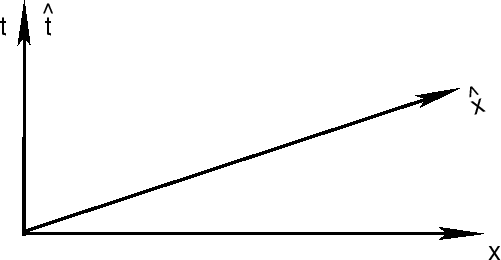 |
V chastnosti iz principa otnositel'nosti Galileya vytekal zakon slozheniya
skorostei:
| (1.2) |
Zakony mehaniki ostayutsya neizmennymi takzhe v sistemah koordinat, osi kotoryh povernuty drug otnositel'no druga. Poskol'ku astronomy - nablyudateli s preobrazovaniyami tipa povorota imeyut delo povsednevno, obsudim ih bolee podrobno.
1.1.1 Vrasheniya v trehmernom prostranstve
Na yazyke matematiki preobrazovaniya Galileya nazyvayutsya preobrazovaniyami trehmernoi sistemy koordinat. Preobrazovaniya tipa (1.1) nazyvayutsya preobrazovaniem sdviga. Pomimo sdviga v trehmernom prostranstve takzhe chasto ispol'zuyut preobrazovanie vrasheniya.
Rassmotrim vse vrasheniya trehmernogo prostranstva vokrug odnoi fiksirovannoi
tochki - nachala koordinat. V ortogonal'noi sisteme koordinat trehmernogo
prostranstva vrashenie zadaetsya uravneniem
Krome togo, pri vrashenii ostaetsya invariantnoi forma vida:
Poetomu mozhno poluchit' uravnenie dlya koefficentov
matricy vida:
Matricy udovletvoryayushie uravneniyu (1.4) nazyvayutsya ortogonal'nymi matricami. Esli vychislit' determinant obeih chastei
uravneniya (1.4), to poluchim uslovie vida
![]() , chto daet dva vozmozhnyh znaka determinanta:
, chto daet dva vozmozhnyh znaka determinanta:
Znak
Rassmotrim vrasheniya.
Prezhde vsego proanaliziruem dve sistemy koordinat na ploskosti. Odnu
sistemu koordinat budem oboznachat' ![]() , vtoruyu -
, vtoruyu - ![]() . Budem schitat',
chto centry etih sistem sovpadayut, a osi povernuty drug otnositel'no druga
na ugol
. Budem schitat',
chto centry etih sistem sovpadayut, a osi povernuty drug otnositel'no druga
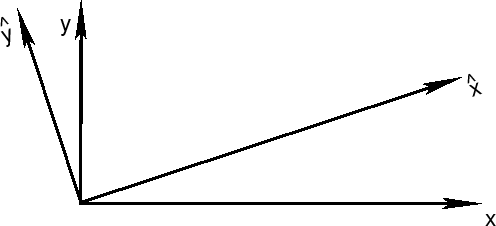
na ugol ![]() protiv chasovoi strelki. Togda preobrazovaniya ot koordinat
bez kryshechki k koordinatam s kryshechkoi zapisyvayutsya v vide sistemy lineinyh
uravnenii:
protiv chasovoi strelki. Togda preobrazovaniya ot koordinat
bez kryshechki k koordinatam s kryshechkoi zapisyvayutsya v vide sistemy lineinyh
uravnenii:
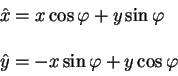
 |
Predstavim eto preobrazovanie v matrichnom vide. Kak vidno iz predydushei
sistemy uravnenii, vrasheniya sovershayutsya vokrug nekotoroi osi. Dlya nachala
vyberem v kachestve osi vrasheniya os' ![]() i sovershim vrashenie na ugol
i sovershim vrashenie na ugol
![]() . Matrica etogo vrasheniya imeet vid:
. Matrica etogo vrasheniya imeet vid:
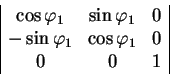
Determinant takoi matricy raven edinice.
Matematiki harakterizuyut vrashenie kak nekotoryi vektor, napravlennyi vdol' osi vrasheniya i ravnyi po velichine uglu povorota. Dlya astronomov bolee privychnym yavlyaetsya predstavlenie vrasheniya v vide treh posledovatel'nyh polozhitel'nyh vrashenii na ugly Eilera1.1. Rassmotrim ih podrobnee.
Polnoe vrashenie mozhet byt' predstavleno treh vrashenii. Pervoe - vrashenie
![]() 1.2na ugol
1.2na ugol ![]() vokrug osi
vokrug osi ![]() , v rezul'tate kotorogo os'
, v rezul'tate kotorogo os'
![]() zaimet novoe polozhenie
zaimet novoe polozhenie ![]() . Zatem vrashenie
. Zatem vrashenie ![]() vokrug novoi
osi
vokrug novoi
osi ![]() na ugol
na ugol ![]() v rezul'tate kotorogo os'
v rezul'tate kotorogo os' ![]() zaimet
novoe polozhenie
zaimet
novoe polozhenie ![]() , i, nakonec, vrashenie
, i, nakonec, vrashenie ![]() vokrug novoi
osi
vokrug novoi
osi ![]() v rezul'tate kotorogo os'
v rezul'tate kotorogo os' ![]() vnov' peremestitsya na
ugol
vnov' peremestitsya na
ugol ![]() :
:
| (1.5) |
Elementy polnoi matricy vrasheniya
![]() mozhno naiti kak proizvedenie treh matric povorotov vokrug osei
mozhno naiti kak proizvedenie treh matric povorotov vokrug osei ![]() ,
, ![]() ,
,
![]() :
:
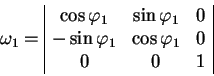 |
(1.6) |
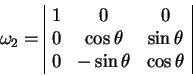 |
(1.7) |
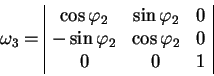 |
(1.8) |
Pri peremnozhenii matric neobhodimo pomnit', chto oni peremnozhayutsya v obratnom poryadke. Peremnozhiv matricy, poluchim:
Pri vrasheniyah ugly
Vrashenie (1.9) imeet obratnyi element. Obratnyi element - eto
vrashenie na takie ugly, kotorye privodyat sistemu koordinat v prezhnee
polozhenie. On zadaetsya drugim
vrasheniem, kotoroe sovershaetsya na ugly Eilera
![]() ,
, ![]() ,
,
![]() .
.
Ostaetsya tol'ko dobavit', chto vrasheniya obrazuyut gruppu. Elementami gruppy yavlyayutsya povoroty na ugly Eilera. Gruppa topologicheski ekvivalentna sharu, u kotorogo otozhdestvleny diametral'no protivopolozhnye tochki.
1.1.2 Preobrazovaniya na moment nablyudeniya
V kachestve primera privedem matricu preobrazovaniya ot koordinat nebesnyh tel, zadannyh v katalogah k tekushim koordinatam na dannyi moment nablyudenii.
V katalogah obychno privodyatsya neskol'ko harakteristik nekotoroi zvezdy, dve
iz kotoryh - koordinaty zvezdy (ee polozhenie) na nebesnoi sfere ![]() (pryamoe voshozhdenie) i
(pryamoe voshozhdenie) i ![]() (sklonenie) privedennye na opredelennuyu
epohu. Drugimi slovami, ukazyvaetsya polozhenie zvezdy na opredelennyi
moment vremeni, skazhem, na 1 yanvarya 2000 goda. Krome ukazaniya epohi,
neobhodimo opredelit' samu sistemu koordinat i ukazat' nachalo otscheta
koordinat1.3.
(sklonenie) privedennye na opredelennuyu
epohu. Drugimi slovami, ukazyvaetsya polozhenie zvezdy na opredelennyi
moment vremeni, skazhem, na 1 yanvarya 2000 goda. Krome ukazaniya epohi,
neobhodimo opredelit' samu sistemu koordinat i ukazat' nachalo otscheta
koordinat1.3.
Polyus mira - tochka, na kotoruyu opiraetsya polyarnaya os', vokrug kotoroi vrashaetsya Zemlya - estestvennaya os' dlya sistemy koordinat. Zvezdy v techenii nochi menyayut svoe polozhenie na nebe (fakt izvestnyi kazhdomu, kto hot' raz nablyudal za nochnym nebom), lish' obna tochka ostaetsya nepodvizhnoi - polyus mira. Naibolee blizko k polyusu (no ne tochno v polyuse) nahoditsya Polyarnaya zvezda. Formal'no polyarnaya os' opredelyaetsya kak os', provedennaya cherez centr sistemy koordinat, parallel'naya osi vrasheniya Zemli [1]. Perpendikulyarno polyarnoi osi lezhit ploskost' ekvatora.
V astronomii istoricheski vybirana sfericheskaya sistema koordinat svyazannaya s vrasheniem Zemli. Polyarnaya os' i ekvator sluzhat osnovnymi elementami etoi sistemy koordinat. Ugol, kotoryi otschityvaetsya v plsokosti ekvatora nazyvaetsya pryamym voshozhdeniem, a ugol, kotoryi otschityvaetsya vdol' meridiana ot ploskosti ekvatora nazyvaetsya skloneniem. Povtorim, chto takaya sistema nebesnyh koordinat voznikla istoricheski v drevnem mire i sohranyaetsya v astronomii do sih por.
Ploskost' ekvatora (ili polozhenie polyarnoi osi) opredelyaet nachalo otscheta
ugla po skloneniyu. Vtoraya osnovnaya tochka sistemy koordinat, nachalo otscheta
vybiraetsya dlya togo, chtoby ukazat' tochku ot kotoroi otschityvaetsya vrashenie
Zemli. Takaya tochka istoricheski byla vybrana kak tochka peresecheniya
nebesnogo ekvatora i ekliptiki. Ekvator - ploskost' perpendikulyarnaya
polyarnoi osi i prekrasno podhodit dlya zadaniya uglovoi koordinaty. Krome
sutochnogo vrasheniya Zemlya ispytyvaet eshe i godovoe vrashenie vokrug Solnca. V
takom godovom vrashenii sushestvuet polyus ekliptiki (os' orbity Zemli vokrug
Solnca) i ploskost' ekliptiki, kotoraya perpendikulyarna polyarnoi osi
ekliptiki. Ekvator i ekliptika nakloneny drug otnositel'no druga na ugol
primerno ![]() , tochka peresecheniya ispol'zuetsya dlya opredeleniya
nachala otscheta pryamogo voshozhdeniya. Ostaetsya dobavit', chto v matematicheskoi
fizike, v sfericheskoi sisteme koordinat, pryamoe voshozhdenie
, tochka peresecheniya ispol'zuetsya dlya opredeleniya
nachala otscheta pryamogo voshozhdeniya. Ostaetsya dobavit', chto v matematicheskoi
fizike, v sfericheskoi sisteme koordinat, pryamoe voshozhdenie ![]() oboznachaetsya obychno
oboznachaetsya obychno ![]() , ekvivalentom vtoroi astronomicheskoi
koordinaty - skloneniya
, ekvivalentom vtoroi astronomicheskoi
koordinaty - skloneniya ![]() yavlyaetsya sfericheskaya koordinata
yavlyaetsya sfericheskaya koordinata
![]() .
.
Takoe opredelenie astronomicheskoi sistemy koordinat sohranyalos' v techenie
mnogih vekov. V poslednee desyatiletie proizoshlo sushestvennoe izmenenie. V
1991 g. Mezhdunarodnyi Astronomicheskii Soyuz (MAS ili IAU - angliiskaya
abreviatura) prinyal novuyu astronomicheskuyu sistemu koordinat osnovannuyu na
nablyudeniyah radioistochnikov. Etu sistemu nazvali ICRF 1.4. Eto vysokotochnaya sistema koordinat,
dostatochno skazat', chto sovremennaya tochnost' polozhenii tak nazyvaemyh
opredelyayushih istochnikov - desyatki mikrosekund dugi. Po opredeleniyu sistemy
ICRF v kachestve ekvatora vybiraetsya ploskost', kotoraya sovpadaet so srednim
ekvatorom na epohu J2000.0, a takzhe v kachestve polyarnoi osi vybiraetsya os'
sovpadayushaya s polyarnoi os'yu kataloga FK5. Takim obrazom, nachalo otscheta
skloneniya opredelyaetsya takzhe ot ekvatora novoi sistemy. Neskol'ko po
drugomu opredelyaetsya tochka otscheta pryamogo voshozhdeniya. V sootvetstvii s
rekomendaciyami IAU nachalo otscheta po ![]() teper' vybiraetsya sledushim
obrazom. Ono vybiraetsya kak mozhno blizhe k dinamicheskoi tochke vesennego
ravnodenstviya na epohu J2000.0, hotya i drugim sposobom. A imenno, nachalom
otscheta vybrano srednee polozhenie 23 radioistochnikov, vhodyashih v spisok
istochnikov, opredelyayushih ICRF. Prichem v radiokatalogah, eti istochniki
smesheny tak, chtoby pryamoe voshozhdenie kvazara 3C273 B sovpadalo s
opticheskoi koordinatoi
teper' vybiraetsya sledushim
obrazom. Ono vybiraetsya kak mozhno blizhe k dinamicheskoi tochke vesennego
ravnodenstviya na epohu J2000.0, hotya i drugim sposobom. A imenno, nachalom
otscheta vybrano srednee polozhenie 23 radioistochnikov, vhodyashih v spisok
istochnikov, opredelyayushih ICRF. Prichem v radiokatalogah, eti istochniki
smesheny tak, chtoby pryamoe voshozhdenie kvazara 3C273 B sovpadalo s
opticheskoi koordinatoi ![]() etogo kvazara.
etogo kvazara.
Zvezdy obladayut sobstvennym dvizheniem, poetomu ih polozheniya menyayutsya, izmenenie polozheniya harakterizuetsya sobstvennymi dvizheniyami (uglovymi skorostyami zvezd po nebu). Pomimo etogo, individual'nogo dlya kazhdoi zvezdy dvizheniya, sushestvuet edinoe dvizhenie vsei nebesnoi cistemy. Eto dvizhenie svyazano s izmeneniem orientacii Zemli v kosmicheskom prostranstve. Sushestvuet po krainei mere tri dvizheniya - precessiya, nutaciya i dvizheniya polyusa Zemli. Esli pervye dva dvizheniya yavlyayutsya deteminirovannymi i mogut byt' predskazany s vysokoi stepen'yu tochnosti, to tret'e dvizhenie - dvizhenie polyusa - yavlyaetsya stohasticheskim. Nezavisimo ot prirody etih dvizhenii oni ekvivalentny vrasheniyam na nekotorye ugly Eilera. Rassmotrim kak eto mozhno sdelat'.
Osi dekartovoi sistemy koordinat v nekotoruyu tekushuyu epohu ![]() nablyudenii
mozhno opredelit' cherez povoroty osei toi zhe dekartovoi sistemy koordinat po
otnosheniyu k osyam v druguyu epohu sootvetstvuyushuyu nachalu otscheta kak
nablyudenii
mozhno opredelit' cherez povoroty osei toi zhe dekartovoi sistemy koordinat po
otnosheniyu k osyam v druguyu epohu sootvetstvuyushuyu nachalu otscheta kak
Zdes' my napisali tol'ko matricy sootvetstvuyushie nutacii ![]() i
precessii
i
precessii ![]() . Vektora
. Vektora ![]() i
i ![]() oboznachayut
edinichnye vektora v epohi
oboznachayut
edinichnye vektora v epohi ![]() i
i ![]() sootvetstvenno. Po soglasheniyu v
astronomii pervyi vektor
sootvetstvenno. Po soglasheniyu v
astronomii pervyi vektor ![]() nazyvayut srednim vektorom (v
epohu
nazyvayut srednim vektorom (v
epohu ![]() ), a vtoroi -
), a vtoroi - ![]() istinnym edinichnym vektorom v epohu
istinnym edinichnym vektorom v epohu
![]() . Eti opredeleniya "srednii" i "istinnyi" ispol'zuyut takzhe i dlya drugih
astronomicheskih terminov, opredelyaya takim obrazom polozheniya zvezd, orty
sistem koordinat, nebesnyi ekvator, polozhenie tochki vesennego
ravnodenstviya, polyus i t.p.
. Eti opredeleniya "srednii" i "istinnyi" ispol'zuyut takzhe i dlya drugih
astronomicheskih terminov, opredelyaya takim obrazom polozheniya zvezd, orty
sistem koordinat, nebesnyi ekvator, polozhenie tochki vesennego
ravnodenstviya, polyus i t.p.
Matrica precessii ![]() v uravnenii (1.10) predstavlyaet vrashenie
za schet obshei precessii za period vremeni
v uravnenii (1.10) predstavlyaet vrashenie
za schet obshei precessii za period vremeni ![]() . Dlya pravyh
ekvatorial'nyh sistem koordinat (pervaya os' napravlena v tochku vesennego
ravnodenstviya, tret'ya os' perpendikulyarna nebesnomu ekvatoru) vrashenie
opredelyaetsya tremya posledovatel'nymi povorotami:
. Dlya pravyh
ekvatorial'nyh sistem koordinat (pervaya os' napravlena v tochku vesennego
ravnodenstviya, tret'ya os' perpendikulyarna nebesnomu ekvatoru) vrashenie
opredelyaetsya tremya posledovatel'nymi povorotami:
Zdes' matricy ![]() yavlyayutsya vrasheniyami vokrug osi
yavlyayutsya vrasheniyami vokrug osi ![]() , tak chto
, tak chto
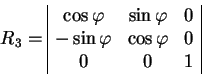 |
(1.12) |
otmetim, chto po sravneniyu s matematicheskim opredeleniem ugla Eilera
![]() povorot zdes' vybran v druguyu storonu.
povorot zdes' vybran v druguyu storonu.
Otmetim takzhe povorot ![]() osushestvlyaetsya ne vokrug osi osi
osushestvlyaetsya ne vokrug osi osi ![]() , a vokrug
osi
, a vokrug
osi ![]() :
:
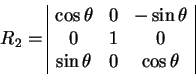 |
(1.13) |
Ugly ![]() ,
, ![]() ,
, ![]() yavlyayutsya funkciyami vremeni, oni
predstavlyayutsya v vide mnogochlenov [1]:
yavlyayutsya funkciyami vremeni, oni
predstavlyayutsya v vide mnogochlenov [1]:
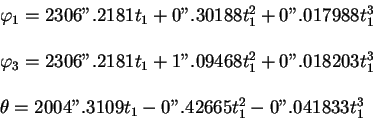 |
(1.14) |
Zdes' ![]() - J2000.0 vyrazheno v yulianskih stoletiyah vremennoi shkaly TDB
(abbreviatura TDB oznachaet dinamicheskoe baricentricheskoe vremya, poodrobnee ob
opredelenii razlichnyh siistem vremeni v astronomii mozhno budet prochitat'
v knige V.E.Zharova).
- J2000.0 vyrazheno v yulianskih stoletiyah vremennoi shkaly TDB
(abbreviatura TDB oznachaet dinamicheskoe baricentricheskoe vremya, poodrobnee ob
opredelenii razlichnyh siistem vremeni v astronomii mozhno budet prochitat'
v knige V.E.Zharova).
Matrica ![]() predstavlyaet vrashenie obuslovlennoe nutaciei. Dlya
ekvatorial'noi sistemy koordinat ona zadaetsya sledushim uravneniem:
predstavlyaet vrashenie obuslovlennoe nutaciei. Dlya
ekvatorial'noi sistemy koordinat ona zadaetsya sledushim uravneniem:
gde ![]() - srednii naklon ekliptiki,
- srednii naklon ekliptiki,
![]() ,
,
![]() - komponenty nutacii po naklonu i dolgote. Naklon ekliptiki
k ekvatoru
- komponenty nutacii po naklonu i dolgote. Naklon ekliptiki
k ekvatoru ![]() yavlyaetsya funkciei vremeni i vychislyaetsya v vide
mnogochlena.
yavlyaetsya funkciei vremeni i vychislyaetsya v vide
mnogochlena.
Dlya preobrazovaniya koordinat ot dekartovoi sistemy k ekvatorial'noi sisteme
koordinat mozhno ispol'zovat', naprimer, uravnenie dlya edinichnogo vektora
ukazyvayushego napravlenie na nebesnyi istochnik:
My sdelali tol'ko preobrazovanie ot srednei sistemy koordinat k istinnoi
ekvatorial'noi sisteme koordinat. Neobhodimo takzhe sdelat' preobrazovanie
ot istinnoi ekvatorial'noi sistemy koordinat k zemnoi sisteme koordinat, v
kotoroi, sobstvenno, i vedutsya nablyudeniya. Dlya etogo pridetsya sdelat'
preobrazovanie vida:
zdes' ![]() - matrica opisyvayushee sutochnoe vrashenie Zemli, v kotoruyu,
kstati, vhodit i dvizhenie polyusa, a
- matrica opisyvayushee sutochnoe vrashenie Zemli, v kotoruyu,
kstati, vhodit i dvizhenie polyusa, a ![]() edinichnyi vektor zemnoi
sistemy koordinat. Matrica
edinichnyi vektor zemnoi
sistemy koordinat. Matrica ![]() zadaetsya v vide proizvedeniya treh
matric - dve iz kotoryh opisyvayut dvizhenie polyusa, a tret'ya opredelyaetsya
chasovym uglom istinnogo vesennego ravnodenstviya, kotoroe otschityvaetsya ot
Grinvichskogo meridiana, etot chasovoi ugol nazyvaetsya takzhe istinnym
Grinvichskim zvezdnym vremenem (GAST). Parametry dvizheniya polyusa
otschityvayutsya otnositel'no odnoi iz osei uslovnoi zemnoi sistemy koordinat.
zadaetsya v vide proizvedeniya treh
matric - dve iz kotoryh opisyvayut dvizhenie polyusa, a tret'ya opredelyaetsya
chasovym uglom istinnogo vesennego ravnodenstviya, kotoroe otschityvaetsya ot
Grinvichskogo meridiana, etot chasovoi ugol nazyvaetsya takzhe istinnym
Grinvichskim zvezdnym vremenem (GAST). Parametry dvizheniya polyusa
otschityvayutsya otnositel'no odnoi iz osei uslovnoi zemnoi sistemy koordinat.
Preobrazovaniya tipa (1.10, 1.11, 1.15) opredelyayut preobrazovaniya koordinat zvezd ot polozhenii ukazannyh v katalogah, na moment vremeni nablyudenii. Kak vidno iz privedennyh uravnenii, dlya vysokotochnyh nablyudenii tipa RSDB - nablyudenii, privedenie istochnikov na mesto soglasno uravneniyam (1.10, 1.11, 1.15) yavlyaetsya neobhodimym usloviem dlya uspeshnyh nablyudenii, poskol'ku raznica ot epohi odin god uzhe privodit k znachitel'nomu uhodu nebesnogo istochnika ot polozheniya ukazannogo v tabliicah. Prichem v sluchae RSDB nablyudenii proizvoditsya redukciya ot zemnoi sistemy koordinat k nebesnoi sisteme.
Takie preobrazovaniya yavlyayutsya pervym shagom na puti redukcii nebesnyh istochnikov na istinnoe polozhenie. Zdes' oni privedeny dlya polnoty. V dal'neishem privedenie na istinnoe polozhenie (redukciya) budet obobshena na sluchai ucheta relyativistskih popravok, kotorye izmenyat' trivial'nye uravneniya tipa (1.10, 1.11, 1.15).
1.2 Trudnosti klassicheskoi mehaniki pri opisanii rasprostraneniya sveta
Princip otnositel'nosti Galileya sygral bol'shuyu rol' v sozdanii mehaniki kak tochnoi nauki.
Fizika razvivalas', posle mehaniki byli otkryty zakony optiki i sozdana teoriya elektromagnitnogo polya. Byl eksperimental'no otkryt fakt, chto skorost' sveta - samogo bystrogo dvizheniya v nashem mire ne zavisit ot skorosti dvizheniya istochnika sveta.
Etot fakt yavno protivorechil zakonu slozheniya skorostei i principu otnositel'nosti Galileya. Bolee togo, princip otnositel'nosti Galileya protivorechil uravneniyam elektrodinamiki i elektromagnitnogo polya.
Osnovnaya trudnost', kotoruyu nado bylo preodolet putem primeneniya principa otnositel'nosti k elektrodinamike, zaklyuchalas' v tom, chto nado bylo soglasovat' dva protivorechyashih drug drugu utverzhdeniya:
- Soglasno klassicheskoi mehanike skorost' lyubogo tela otnositel'no dvuh
nablyudatelei dvigayushihsya otnositel'no drug druga raznaya.
- Skorost' sveta, soglasno opytu, ne zavisit ot dvizheniya nablyudatelya ili istochnika sveta i yavlyaetsya mirovoi fizicheskoi postoyannoi.
Pervoe utverzhdenie nosilo teoreticheskii, konceptual'nyi harakter, togda kak vtoroe bylo osnovano na opyte. Poskol'ku vtoroe utverzhdenie osnovano na opyte, to ego cennost' vyshe i sleduet otkazat'sya otpervogo utverzhdeniya i tem samym ot teh predstavlenii o prostranstve i vremeni, kotorye byli prinyaty ranee.
Odno iz predstavlenii ot kotoryh my otkazyvaemsya - n'yutonovskoe ponyatie odnovremennosti. N'yuton, postuliruya sushestvovanie absolyutnogo vremeni, ili absolyutnoi dlitel'nosti, pisal: "vremya techet vsegda odinakovo, bezotnositel'no k chemu libo vneshnemu".
V 1905 g. A.Einshteinom byl sformulirovan princip special'noi otnositel'nosti, kotoryi byl spravedliv dlya primeneniya k teorii elektrodinamiki i teorii elektromagnitnogo polya i zalozhil novyi vzglyad na prostranstvo i vremya.
1.3 Special'naya teoriya otnositel'nosti
V special'noi teorii otnositel'nosti poyavlyaetsya novoe opredelenie ponyatiya odnovremennosti.
Odnovremennost' sobytii. Dva sobytiya proishodyat v odin i tot zhe
moment vremeni sinhronizirovannyh chasov v razlichnyh tochkah prostranstva.
Voznikaet novoe opredelenie sinhronizovannyh chasov. Pust' v tochkah ![]() i
i
![]() est' chasy. Opredelyaem, chto vremya prohozhdeniya sveta iz
est' chasy. Opredelyaem, chto vremya prohozhdeniya sveta iz ![]() v
v ![]() ravno
vremeni prohozhdeniya sveta iz
ravno
vremeni prohozhdeniya sveta iz ![]() v
v ![]() . Poyasnim eto na ris. 1.3.
Pust' v moment vremeni
. Poyasnim eto na ris. 1.3.
Pust' v moment vremeni ![]() iz
iz ![]() posylaetsya svetovoi signal, on
dostigaet tochki
posylaetsya svetovoi signal, on
dostigaet tochki ![]() v moment vremeni
v moment vremeni ![]() , otrazhaetsya i dostigaet tochki
, otrazhaetsya i dostigaet tochki
![]() v moment vremeni
v moment vremeni ![]() . Chasy po opredeleniyu idut v tochkah
. Chasy po opredeleniyu idut v tochkah ![]() i
i ![]() sinhronno esli
sinhronno esli
| (1.18) |
Prinimayutsya takzhe dve aksiomy:
- Esli chasy
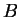 idut sinhronno s chasami
idut sinhronno s chasami 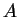 , to chasy
, to chasy 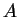 idut sinhronno
s chasami
idut sinhronno
s chasami 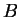 .
.
- Esli chasy
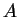 idut sinhronno s chasami
idut sinhronno s chasami 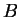 , a chasy
, a chasy 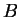 idut sinhronno
s chasami
idut sinhronno
s chasami 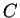 , to chasy
, to chasy 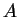 idut sinhronno s chasami
idut sinhronno s chasami 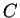 .
.
A.Einshtein takzhe sformuliroval dva principa: princip otnositel'nosti i princip postoyanstva skorosti sveta.
Princip otnositel'nosti
Zakony, po kotorym izmenyayutsya sostoyaniya fizicheskih sistem, ne zavisyat ot
togo, k kotoroi iz dvuh koordinatnyh sistem, dvizhushihsya drug otnositel'no
druga pryamolineino i ravnomerno, eti izmeneniya otnosyatsya.
Princip postoyanstva skorosti sveta
Kazhdyi luch sveta dvizhetsya v izbrannoi sisteme koordinat so skorost'yu ![]() ,
nezavisimo ot togo, ispuskaetsya li etot luch pokoyashimsya ili dvizhushimsya
telom. Pri etom skorost' lucha sveta opredelyaetsya soglasno:
,
nezavisimo ot togo, ispuskaetsya li etot luch pokoyashimsya ili dvizhushimsya
telom. Pri etom skorost' lucha sveta opredelyaetsya soglasno:
Nesmotrya na abstraktnost' eti opredeleniya osobenno vazhny dlya interpretacii astronomicheskih nablyudenii. Prodemonstriruem eto utverzhdenie na prostom primere.
1.3.1 Sverhsvetovye dvizheniya i ih interpretaciya
Nekotoroe vremya nazad on predstavlyal iz sebya zagadku dlya soobshestva astronomov, kotoraya brosila vyzov teorii otnositel'nosti.
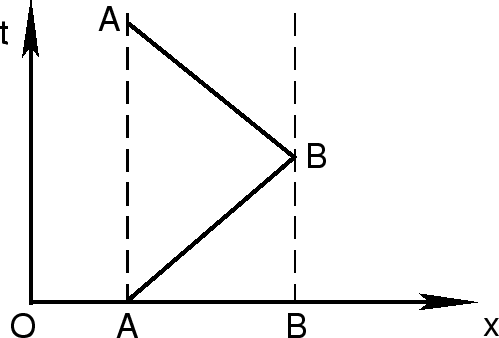
Rassmotrim ris. 1.4. Pust' iz istochnika ![]() vybrasyvaetsya
materiya (naprimer, sgustki plazmy). Eti sgustki letyat pod uglom
vybrasyvaetsya
materiya (naprimer, sgustki plazmy). Eti sgustki letyat pod uglom ![]() k
napravleniyu na nablyudatelya. Chemu ravna vidimaya poperechnaya skorost'
peremesheniya etih sgustkov po nebu?
k
napravleniyu na nablyudatelya. Chemu ravna vidimaya poperechnaya skorost'
peremesheniya etih sgustkov po nebu?
Eta zadacha voznikla pri analize t.n. sverhsvetovyh dvizhenii v kvazarah. Iz mnogih kvazarov nablyudayutsya vybrosy bol'shogo kolichestva veshestva. Pri nablyudeniyah vybrosov astronomy izmeryali ih uglovye skorosti. Po ih krasnomu smesheniyu opredelyalos' rasstoyanie do kvazarov. Umnozhaya rasstoyanie do kvazarov na uglovuyu skorost' peremesheniya vybrosov po nebu astronomy poluchali poperechnuyu skorost' dvizheniya vybrosa. Standartnaya procedura dala neozhidannyi rezul'tat. V neskol'kih sluchayah poperechnaya skorost' dvizheniya vybrosov okazalas' bol'she skorosti sveta!
Astronomy byli postavleny pered nelegkoi zadachei. Kazalos', chto nado sdelat' vybor iz dvuh, odinakovo plohih variantov. Pervyi - priznat', chto v prirode mogut sushestvovat' skorosti bol'she, chem skorost' sveta. Prosto oni ne vstrechayutsya ni v solnechnoi sisteme, ni tem bolee v laboratornyh usloviyah. Vtoroi variant - priznat', chto krasnoe smeshenie v kvazarah - ne rezul'tat kosmologicheskogo krasnogo smesheniya, a sledovatel'no kvazary mogut byt' raspolozheny k nam gorazdo blizhe. Oba varianta, kak ya uzhe skazal byli plohimi.
Odnako, reshenie zadachi okazalos' vozmozhnym v ramkah kak special'noi teorii otnositel'nosti, tak i v ramkah kosmologicheskogo scenariya sushestvovaniya kvazarov. Reshenie, naidennoe P.Sheierom, osnovyvalos' na pravil'nom obrashenii s ponyatiem odnovremennosti.
Rassmotrim dvizhenie odnogo sgustka veshestva. Pust' v moment vremeni ![]() on vybrasyvaetsya iz istochnika
on vybrasyvaetsya iz istochnika ![]() pod uglom
pod uglom ![]() k napravleniyu
k napravleniyu ![]() .
Sgustok predstavlyaet iz sebya plazmu, izluchayushuyu radiovolny. Poetomu
odnovremenno s vybrosom sgustka, k nablyudatelyu po napravleniyu
.
Sgustok predstavlyaet iz sebya plazmu, izluchayushuyu radiovolny. Poetomu
odnovremenno s vybrosom sgustka, k nablyudatelyu po napravleniyu ![]() idet
svetovoi signal (fotony radiochastoty) o tom, chto sgustok vybroshen. Sgustok
dvizhetsya so skorost'yu
idet
svetovoi signal (fotony radiochastoty) o tom, chto sgustok vybroshen. Sgustok
dvizhetsya so skorost'yu ![]() i cherez nekotoryi interval vremeni
i cherez nekotoryi interval vremeni ![]() okazyvaetsya v polozhenii
okazyvaetsya v polozhenii ![]() . K etomu vremeni svetovoi signal proshel put'
. K etomu vremeni svetovoi signal proshel put'
![]() i okazalsya v tochke
i okazalsya v tochke ![]() . Sgustok prodolzhaet izluchat' radiofotony.
Poetomu cherez vremya
. Sgustok prodolzhaet izluchat' radiofotony.
Poetomu cherez vremya ![]() iz tochki
iz tochki ![]() v napravlenii nablyudatelya vnov' idet
signal o tom, chto sgustok dostig
v napravlenii nablyudatelya vnov' idet
signal o tom, chto sgustok dostig ![]() . Postroim vspomogatel'nyi
perpendikulyar iz
. Postroim vspomogatel'nyi
perpendikulyar iz ![]() na pryamuyu soedinyayushuyu
na pryamuyu soedinyayushuyu ![]() i
i ![]() . Vychislim
prodol'noe rasstoyanie
. Vychislim
prodol'noe rasstoyanie ![]() mezhdu tochkami
mezhdu tochkami ![]() i
i ![]() . Ono
ravnyaetsya:
. Ono
ravnyaetsya:
Poperechnoe rasstoyanie mezhdu tochkami ![]() i
i ![]() ravnyaetsya velichine:
ravnyaetsya velichine:
Ugol mezhdu pryamymi ![]() i
i ![]() nichtozhno mal (my schitaem, chto rasstoyanie do
kvazara znachitel'no prevoshodit vse ostal'nye masshtaby rassmatrivaemoi
zadachi). Poetomu signaly o tom, chto sgustok vyshel iz istochnika
nichtozhno mal (my schitaem, chto rasstoyanie do
kvazara znachitel'no prevoshodit vse ostal'nye masshtaby rassmatrivaemoi
zadachi). Poetomu signaly o tom, chto sgustok vyshel iz istochnika ![]() i prishel
v tochku
i prishel
v tochku ![]() pridut k nablyudatelyu cherez interval vremeni
pridut k nablyudatelyu cherez interval vremeni
![]() , a poperechnoe rasstoyanie proidennoe etim sgustkom budet sostavlyat'
, a poperechnoe rasstoyanie proidennoe etim sgustkom budet sostavlyat'
![]() . Teper' mozhno razdelit' poperechnoe rasstoyanie
na interval vremeni
mezhdu sobytie 1 (vyhod sgustka iz istochnika) i sobytiem 2 (poyavlenie
sgustka v tochke
. Teper' mozhno razdelit' poperechnoe rasstoyanie
na interval vremeni
mezhdu sobytie 1 (vyhod sgustka iz istochnika) i sobytiem 2 (poyavlenie
sgustka v tochke ![]() ) poluchaem vidimuyu skorost' peremesheniya sgustka po nebu:
) poluchaem vidimuyu skorost' peremesheniya sgustka po nebu:
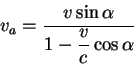
Otsyudya vidno, chto kogda skorost' dvizheniya sgustka blizka k skorosti sveta,
a ugol ![]() mal, vidimaya skorost' dvizheniya sgustka po nebu mozhet
znachitel'no prevyshat' skorost' sveta.
mal, vidimaya skorost' dvizheniya sgustka po nebu mozhet
znachitel'no prevyshat' skorost' sveta.
Rassmotrim podrobnee usloviya pri kotoryh vidimaya skorost' peremesheniya
sgustka po nebu budet prevyshat' skorost' sveta. Itak, budem schitat', chto
Poskol'ku trigonometricheskie funkcii ne prevyshayut 1, to poyavlyaetsya pervoe uslovie dlya skorosti sgustka
Znachit, kogda ugol ![]() nahoditsya v predelah 0
nahoditsya v predelah 0 ![]()
![]() nablyudatel' vidit sverhsvetovoe peremeshenie sgustka po nebu.
nablyudatel' vidit sverhsvetovoe peremeshenie sgustka po nebu.
V etom primere sverhsvetovoe dvizhenie bylo ob'yasneno bez vyhoda za ramki special'noi teorii otnositel'nosti. Zdes' osnovnuyu rol' sygralo pravil'noe obrashenie s ponyatiem odnovremennyh sobytii ( v dannom sluchae odnovremennyi prihod signalov k nablyudatelyu).
<< Vvedenie | Oglavlenie | 2. Special'naya teoriya otnositel'nosti >>
|
Publikacii s klyuchevymi slovami:
Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni
Publikacii so slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |