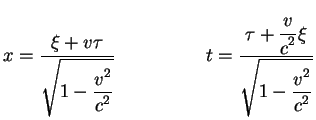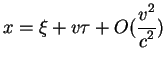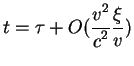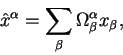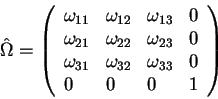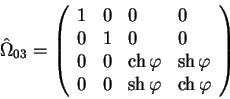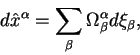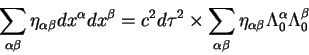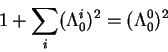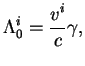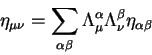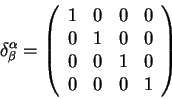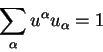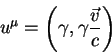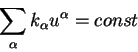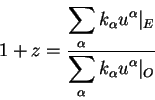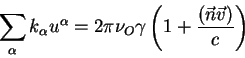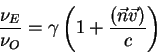Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu
Teoriya otnositel'nosti dlya astronomov
<< 1. Principy otnositel'nosti | Oglavlenie | 3. Uskorennye sistemy otscheta >>

Razdely

2. Special'naya teoriya otnositel'nosti

Astronomy nablyudayut elektromagnitnoe izluchenie (svet) nebesnyh istochnikov v razlichnyh diapazonah spektra. Hotya samo izluchenie harakterizuetsya celym naborom parametrov, dlya astronomii vazhny sledushie: napravlenie prihoda sveta, ego chastota, a takzhe inogda intensivnost'. Dlya bol'shinstva astronomicheskih zadach volnovaya priroda elektromagnitnogo izlucheniya takzhe ne igraet reshayushei roli. Obychno bol'shinstvo zadach s uspehom mozhet byt' resheno v priblizhenii geometricheskoi optiki prinimaemyh fotonov, vklyuchaya dazhe fotony radiodiapazona. Lish' neskol'ko zadach trebuyut ucheta volnovoi prirody, naprimer, zadachi interferometrii. Odnako, dlya vychisleniya mnogih zadach interferometrii dostatochno znaniya tol'ko parametrov izlucheniya, naidennyh v predele geometricheskoi optiki. Poetomu my budem rabotat' s osnovnym parametrom harakterizuyushimi izluchenie v predele geometricheskoi optiki - volnovym vektorom izlucheniya. Napravlenie prihoda luchei sveta i ego chastota v special'noi teorii otnositel'nosti ob'edinyayutsya v edinyi vektor - 4$^x$ impul's fotona.

Poetomu odnoi iz osnovnyh nashih zadach budem vyvod uravnenii redukcii i ih resheniya dlya chetyrehmernogo vektora impul'sa fotona.

2.1 Kinematika special'noi teorii otnositel'nosti

Prezhde chem vyvodit' osnovnye kinematicheskie uravneniya STO sformuliruem princip postoyanstva skorosti sveta na yazyke matematiki.

Rassmotrim opyat' dve sistemy, dvizhushiesya ravnomerno i pryamolineino drug otnositel'no druga. Budem schitat', chto sistema $K$ nepodvizhna otnositel'no nablyudatelya, a sistema $\hat K$ dvizhetsya so skorost'yu $v$. Pust' v $K$ iz tochki s koordinatami $(x_1,$ $y_1,$ $z_1)$ v moment $t_1$ vyhodit luch sveta i dostigaet tochki s koordinatami $(x_2,$ $y_2,$ $z_2)$ v moment $t_2$. V sisteme $\hat K$ eti dva sobytiya vyglyadyat sledushim obrazom. V moment $\hat t_1$ iz tochki s koordinatami $(\hat x_1,$ $\hat y_1,$ $\hat z_1)$ vyhodit luch sveta, kotoryi popadaet v tochku s koordinatami $(\hat x_2,$ $\hat y_2,$ $\hat z_2)$ v moment vremeni $\hat t_2$.

Iz uravnenii teorii elektromagnitnogo polya ( uravnenii Maksvella) my znaem, chto prostranstvenno - vremennaya tochka $(x_1,$ $y_1,$ $z_1$, $t_1)$ svyazana s prostranstvenno - vremennoi tochkoi $(x_2,$ $y_2,$ $z_2$, $t_2)$ ravenstvom vida:

\begin{displaymath} (x_1 -x_2)^2 + (y_1 -y_2)^2 +(z_1 -z_2)^2 =c^2 (t_1 -t_2)^2 \end{displaymath} (2.1)

Zdes' $c$ -skorost' sveta. Postulat ob odinakovosti skorosti sveta v obeih sistemah koordinat mozhno sformulirovat' tak, chto ravenstvo (2.1) spravedlivo i v sisteme koordinat $\hat K$:

\begin{displaymath} (\hat x_1 -\hat x_2)^2 + (\hat y_1 -\hat y_2)^2 +(\hat z_1 -\hat z_2)^2 =c^2 (\hat t_1 -\hat t_2)^2 \end{displaymath} (2.2)

Obratim vnimanie, chto v sisteme $\hat K$ uravnenie soderzhit $c$, a ne $\hat c$, poskol'ku dve eti velichiny ravny drug drugu.

Teper' budem schitat', chto tochki 1 i 2 lezhat beskonechno blizko drug k drugu, a takzhe budem schitat', chto interval vremeni dlya rasprostraneniya sveta iz 1 v 2 yavlyaetsya beskonechno malym. Togda upomyanutye ravenstva mozhno zapisat' kak:

\begin{displaymath} dx^2 + dy^2 +dz^2 =c^2 dt^2 \end{displaymath} (2.3)

Vvedem teper' ponyatie 4$^x$ mernogo intervala mezhdu dvumya sobytiyami. Budem nazyvat' pervym sobytiem to, kotoroe proizoshlo v tochke s koordinatami $(x,$ $y,$ $z)$ v moment $t$, a vtorym sobytiem to, kotoroe proizoshlo v tochke s koordinatami $(x+dx,$ $y +dy,$ $z +dz)$ v moment $t +dt$. Opredelim 4$^x$ mernyi interval mezhdu pervym i vtorym sobytiem kak rasstoyanie v psevdoevklidovom prostranstve:

\begin{displaymath} ds^2 =c^2 dt^2 -dx^2 - dy^2 -dz^2 \end{displaymath} (2.4)

Iz invariantnosti skorosti sveta sleduet, chto interval mezhdu dvumya sobytiyami - izlucheniem sveta iz kakoi -libo prostranstvennoi tochki i priemom sveta v drugoi tochke raven nulyu v lyuboi inercial'noi sisteme otscheta. T.e. $ds=0$ v sisteme $K$ i $\hat ds=0$ v sisteme $\hat K$.

4$^x$ mernyi interval yavlyaetsya invariantom pri preobrazovaniyah koordinat, ego velichina ne zavisit ot togo v kakoi sistemah otscheta rassmatrivayutsya koordinaty mezhdu sobytiyami. Vospol'zuemsya etim svoistvom dlya vyvoda pravil'nyh preobrazovanii koordinat mezhdu dvumya sistemami, kotorye dvizhutsya otnositel'no drug druga.

2.1.1 Preobrazovaniya mezhdu inercial'nymi sistemami

Rassmotrim dve dvizhushiesya sistemy koordinat. Iz principa postoyanstva skorosti sveta, a takzhe iz invariantnosti $4^x$ mernogo intervala mozhno zaklyuchit', chto v dvuh sistemah koordinat $K \in (t,x)$ i $\Xi \in (\tau, \xi)$, svyazannyh lineinymi preobrazovaniyami vida 2.1:

$\displaystyle x=\xi \alpha +c\tau \beta$ (2.5)
$\displaystyle ct= c \tau \alpha + \xi \beta$  

dolzhny sovpadat' differencialy intervala mezhdu dvumya sobytiyami:
$\displaystyle ds^2= c^2dt^2- dx^2 \mbox{\hskip1cm v sisteme $K$}$ (2.6)
$\displaystyle ds^2= c^2d\tau^2- d\xi^2 \mbox{\hskip1cm v sisteme $\Xi$}$  

Koefficenty preobrazovaniya $\alpha, \beta$ proshe vsego vybrat' v vide:

$\displaystyle \alpha=\ch \psi$ (2.7)
$\displaystyle \beta =\sh \psi$  

Rassmotrim differencialy (2.5) i podstavim ih v vyrazheniya dlya 4$^x$ mernogo intervala. Legko videt', chto ravenstvo

\begin{displaymath} \ch^2 \psi -\sh^2 \psi=1 \end{displaymath}

obespechivaet invariantnost' intervala:

\begin{displaymath} c^2dt^2-dx^2=c^2d\tau^2 -d\xi^2. \end{displaymath}

Raasmotrim teper' svyaz' ugla $\psi$ v vyrazheniyah dlya giperbolicheskih sinusa i kosinusa so skorost'yu sistemy $\hat K$ otnositel'no sistemy $K$. Rassmotrim dvizhenie centra sistemy $\hat K$ v sisteme koordinat $K$. Centr sistemy koordinat $\Xi$ nahoditsya v tochke $\xi=0$. V sisteme koordinat $K$ tochka $\xi=0$ dvizhetsya soglasno sisteme uravnenii:

$\displaystyle x=c \tau \sh \psi$ (2.8)
$\displaystyle ct= c \tau \ch \psi$  

Otsyuda legko zaklyuchit', chto centr sistemy koordinat $\Xi$ dvizhetsya v sisteme $K$ so skorost'yu:

\begin{displaymath} {\displaystyle x\over\displaystyle ct}={\displaystyle v\over\displaystyle c}=\th \psi \end{displaymath}

Teper' vyrazhaya giperbolicheskie sinus i kosinus cherez giperbolicheskii tangens prihodim k uravneniyam dlya preobrazovaniya koordinat:

$\displaystyle x={\displaystyle\xi +v\tau\over\displaystyle\sqrt{1-{\displaystyl... ...le c^2}\xi\over\displaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}}$ (2.9)

Otmetim, chto preobrazovaniya (2.9) bol'she pohozhi na preobrazovaniya tipa vrasheniya (1.3), a ne preobrazovaniya Galileya (1.1). Rassmotrim teper' predel malyh skorostei, kogda ${\displaystyle v\over\displaystyle c} \ll 1$, razlozhim preobrazovaniya (2.9) v ryad Teilora po stepenyam etogo malogo parametra i ostavim tol'ko lineinye velichiny po ${\displaystyle v\over\displaystyle c} \ll 1$ prenebregaya kvadratichnymi i bolee vysokimi stepenyami otnosheniya vzaimnoi skorosti dvizheniya sistem k skorosti sveta:

$\displaystyle x=\xi +v\tau +O({\displaystyle v^2\over\displaystyle c^2})$ (2.10)
$\displaystyle \qquad$ (2.11)
$\displaystyle t=\tau + O({\displaystyle v^2\over\displaystyle c^2}{\displaystyle\xi\over\displaystyle v})$ (2.12)

Vtoroi chlen v prebrazovanii vremeni vypisan special'no dlya togo, chtoby prodemonstrirovat', chto v preobrazovanii vremeni soderzhatsya sledy ot preobrazovanii Lorenca, no oni vtorogo poryadka po otnosheniyu ${\displaystyle v\over\displaystyle c}$. Takim obrazom, preobrazovaniya Lorenca svodyatsya k preobrazovaniyam Galileya. Poetomu v predele malyh (po sravneniyu so skorost'yu sveta) skorostei zavisimost' koordinaty $Ox$ ot vremeni $\tau$ priobretaet vid preobrazovaniya tipa sdviga, vremya stanovitsya vneshnim parametrom po otnosheniyu k preobrazovaniyam trehmernyh koordinat. Vremya stanovit'sya neizmennym, vneshnee vliyanie na etot parametr otsutstvuet.

2.1.2 Interval sobstvennogo vremeni

Rassmotrim pokoyashuyusya sistemu otscheta $K$. Rassmotrim v nei dva sobytiya, skazhem, kolebanie matematicheskogo mayatnika, pokoyushegosya otnositel'no etoi sistemy. Pervoe sobytie - prohozhdenie mayatnika cherez tochku ravnovesiya, a vtoroe - ego povtornoe prohozhdenie cherez ravnovesnuyu tochku. Prostranstvennoe rasstoyanie mezhdu dvumya sobytiyami ravno nulyu $dx=0$, $dy=0$, $dz=0$. Togda interval mezhdu dvumya etimi sobytiyami opredelyaet interval sobstvennogo vremeni $ds^2=c^2d\tau^2$.

Eto opredelenie prinyatoe v special'noi teorii otnositel'nosti ostaetsya spravedlivym i v obshei teorii otnositel'nosti.

Rassmotrim teper' zavisimost' intervalov vremeni i dliny ot sostoyaniya dvizheniya. Pust' v sisteme $\hat K$ pokoyatsya chasy. Rassmotrim dva sobytiya v sisteme $\hat K$. Pervoe sobytie - pokazanie chasov $\hat t_0=0$ v tochke $\hat x=0$, $\hat y=0$, $\hat z=0$. Vtoroe sobytie - pokazanie chasov $\hat t_1=1$ sek v toi zhe tochke prostranstva. Vremya v sisteme koordinat $\hat K$ mezhdu etimi sobytiyami est' $\tau =t_1- t_0=1$ sek. Interval mezhdu etimi sobytiyami est' $ds=cd\tau=3\cdot 10^{10}$ sm/sek $\times 1$ sek=300 000 km. Naidem vremya, kotoroe proshlo mezhdu etimi sobytiyami v sisteme $K$, v kotoroi pokoitsya nablyudatel' izmerennoe po chasom etogo nablyudatelya. Preobrazovanie vremeni iz sistemy $\hat K$ v sistemu $K$ osushestvlyaetsya po formule:

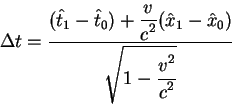
\begin{displaymath} \Delta t={\displaystyle(\hat t_1 -\hat t_0) +{\displaystyle ... ...splaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}} \end{displaymath}

poskol'ku prostranstvennoe rasstoyanie v sisteme $\hat K$ mezhdu dvumya sobytiyami ravno nulyu, a interval vremeni raven $\Delta \hat t=1$ sek, to v sisteme $K$ chasy pokazhut, chto proshlo vremya:

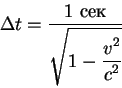
\begin{displaymath} \Delta t={\displaystyle\mbox{1 sek}\over\displaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}} \end{displaymath}

Itak, dlya nablyudatelya, kotoryi pokoitsya v sisteme koordinat $K$ chasy pokazyvayut, chto proshlo bol'she vremeni, chem 1 sek. Eto odin iz samyh neozhidannyh vyvodov special'noi teorii otnositel'nosti. Dlya nespecialistov etot vyvod predstavlyalsya paradoksal'nym i posluzhil odnim iz povodov dlya popytok teoreticheski oprovergnut' special'nuyu teoriyu otnositel'nosti, dokazat' ee vnutrennyuyu protivorechivost'.

Odnim iz naibolee rasprostranennyh sposobov oprovergnut' STO sluzhil t.n. paradoks bliznecov. On formulirovalsya sledushim obrazom.

Rassmotrim dvuh brat'ev - bliznecov. Odin iz nih uletaet na rakete v dlitel'noe puteshestvie. Raketa dvigaetsya so skorost'yu blizkoi k skorosti sveta, tak chto 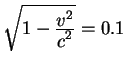$\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}=0.1$ Vtoroi ostaetsya na Zemle. Pervyi brat posle puteshestviya vozvrashaetsya na Zemlyu. Ego sobstvennye chasy pokazyvayut, chto proshlo, skazhem, odin god. Chasy vtorogo brata pokazyvayut, chto proshlo 10 let. Vyvod: brat - bliznec zhivshii na Zemle postarel na 10 let, v to vremya kak ego brat - puteshestvennik postarel tol'ko na odin god.

"Horosho" - govorit zhelayushii oprovergnut' STO. "Teper' davaite rassmotrim situaciyu s tochki zreniya brata - puteshestvennika. S ego tochki zreniya Zemlya dvizhetsya so skorost'yu blizkoi k skorosti sveta, a sledovatel'no, na Zemle chasy dolzhny idti medlennee. Brat - puteshestvennik, vernuvshis' na Zemlyu obnaruzhit, chto u ego brata - blizneca chasy pokazyvayut tol'ko 365 dnei."
"Paradoks!"
vosklicaet oprovergatel',
"Eto dokazyvaet vnutrennyuyu protivorechivost' STO!"
Posle chego delaetsya vyvod, chto STO ne verna.

Razumeetsya, etot vyvod osnovan na oshibke. Oshibka zaklyuchaetsya v tom, chto kosmonavt, puteshestvuyushii na rakete, chast' puti nahoditsya v neinercial'noi sisteme otscheta. Poetomu dve sistemy neekvivalentny. Dokazano eto budet, kogda my poznakomimsya s vychisleniem sobstvennogo vremeni v uskorennyh sistemah otscheta. Poka zhe ogranichimsya ukazaniem na to, chto brat - bliznec ostavshiisya na Zemle, postareet bol'she chem puteshestvennik.

2.1.3 Dlina dvizhushegosya sterzhnya

Rassmotrim teper' kak menyayutsya sobstvennye dliny sterzhnei v dvizhusheisya i pokoyusheisya sistemah otscheta.

Dlya etogo vypishem preobrazovanie prostranstvennoi koordinaty (2.9) iz dvizhusheisya v nepodvizhnuyu sistemu:

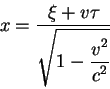\begin{displaymath} x={\displaystyle\xi +v\tau\over\displaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}} \end{displaymath} (2.13)

Razmer sterzhnya v nepodvizhnoi sisteme oboznachim $x_1- x_0=l_p$. V pokoyasheisya sisteme otscheta ego razmer opredelyaetsya vyrazheniem:

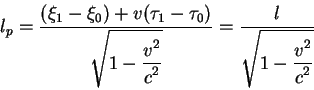\begin{displaymath} l_p={\displaystyle(\xi_1 -\xi_0) +v(\tau_1-\tau_0)\over\disp... ...isplaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}} \end{displaymath} (2.14)

poskol'ku razmer sterzhnya v dvizhusheisya sisteme $l$ neobhodimo opredelyat' v odin i tot zhe moment vremeni $\tau_1=\tau_0$. Poetomu dlina sterzhnya budet maksimal'na v toi sisteme otscheta v kotoroi sterzhen' pokoitsya. V lyuboi drugoi inercial'noi sisteme otscheta, kotoraya dvizhetsya otnositel'no pokoyasheisya so skorost'yu $v$ dlina sterzhnya budet men'she:
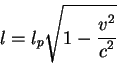\begin{displaymath} l=l_p \sqrt{1-{\displaystyle v^2\over\displaystyle c^2}} \end{displaymath} (2.15)

Pust' sterzhen' dlinoi $l$ v sobstvennoi sisteme otscheta dvizhetsya so skorost'yu $v$ otnositel'no fotoapparata dalekogo nablyudatelya. Za sterzhnem parallel'no emu raspolozhena lineika s nanesennymi metkami dliny, kotoraya pokoitsya otnositel'no nablyudatelya. Napravlenie na fotoapparat sostavlyaet ugol $\theta$ s napravleniem skorosti sterzhnya. Chemu ravna kazhushayasya dlina sterzhnya? Kakaya chast' mernoi lineiki zakryta sterzhnem?

2.2 Obshie preobrazovaniya sistemy koordinat, busty.

Rassmotrim teper' obshie preobrazovaniya sistem koordinat, kotorye vklyuchayut v sebya ne tol'ko chetyrehmernye povoroty svyazyvayushie os' vremeni i odnu iz prostranstvennyh osei, no takzhe i trehmernye vrasheniya. Takie obshie preobrazovaniya pozvolyayut sdelat' redukciyu na moment nablyudenii.

Kak i v paragrafe posvyashennom obsuzhdeniyu vrashenii rassmotrim lineinoe preobrazovanie tipa:

\begin{displaymath} \hat x^{\alpha}=\sum_{\beta} \Omega^{\alpha}_{\beta} x_{\beta}, \end{displaymath} (2.16)

gde $x_{\alpha}$ -koordinaty vektora v sisteme $K$, $\hat x_{\alpha}$ koordinaty togo zhe vektora v sisteme $\hat K$. Matrica $\Omega_{\alpha \beta}$ opredelyaet vrashenie. Budem oboznachat' vrashenie inogda bukvoi $\hat \Omega$, toi zhe, chto i matricu. Krome togo, teper' koordinaty numeruyutsya bukvami grecheskogo alfavita i probegayut znacheniya $\alpha \ni (0, 1, 2, 3)$. Vsyudu nizhe budem priderzhivat'sya etogo pravila. Grecheskie bukvy budut numerovat' chetyre koordinaty (odnu vremennuyu 0 i tri prostranstvennyh 1, 2, 3), latinskie (krome special'no ogovorennyh sluchaev) tri prostranstvennye koordinaty. V svyazi s etim grecheskie indeksy budem inogda imenovat' prostranstvenno - vremennnymi, a latinskie - prostranstvennymi indeksami.

Napishem neskol'ko dopolnitel'nyh uslovii na vrashenie. Teper' preobrazovaniya takogo tipa dolzhny ostavlyat' invariantnoi chetyreh formu vida:

\begin{displaymath} S^2=x_0^2 - x_1^2 -x_2^2 -x_3^2 \end{displaymath} (2.17)

togda takie preobrazovaniya nazyvayutsya preobrazovaniyami Lorenca. Vvedem matricu:

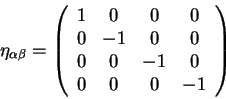\begin{displaymath} \eta_{\alpha \beta}= \left( \begin{array}{cccc} 1& 0& 0& 0 \... ...1& 0& 0 \\ 0& 0& -1& 0 \\ 0& 0& 0& -1 \\ \end{array}\right) \end{displaymath} (2.18)

pri preobrazovaniyah Lorenca imeet mesto ravestvo

\begin{displaymath} \hat \Omega^* \hat \eta \hat \Omega=\hat \eta \end{displaymath}

zdes' $\hat \Omega^*$ oznachaet transponirovannuyu matricu. Otsyuda legko zaklyuchit', chto $Det(\eta)=\pm 1$, sledovatel'no sushestvuet obratnoe preobrazovanie $\hat \eta^{-1}$, kotoroe takzhe yavlyaetsya preobrazovaniem Lorenca. Proizvedenie dvuh preobrazovanii Lorenca takzhe daet preobrazovanie Lorenca, poetomu preobrazovaniya Lorenca obrazuyut gruppu. Uravnenie $S^2=x_0^2 - x_1^2 -x_2^2 -x_3^2 $ opredelyaet v chetyrehmernom prostranstve konus (ego nazyvayut svetovym konusom). Svetovoi konus delit vse prostranstvo - vremya na dve vnutrennie poly konusa, v kotoryh $S^2>0$ i vneshnie oblasti, v kotoryh $S^2<0$.

Pust' $\hat \omega$ - matrica preobrazovaniya (vrashenie) trehmernogo prostranstva. Rassmotrim preobrazovanie v chetyrehmernom prostranstve vida:

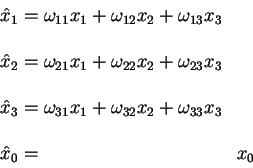
\begin{displaymath} \begin{array}{l} \hat x_1=\omega_{11}x_1 +\omega_{12}x_2 +\o... ...mega_{31}x_1 +\omega_{32}x_2 +\omega_{33}x_3 +} x_0 \end{array}\end{displaymath}

Eto preobrazovanie prinadlezhit gruppe preobrazovanii Lorenca. Ono ostavlyaet bez izmeneniya koordinatu $x_0$ v summe (2.17) i ne menyaet summu $x_1^2 +x_2^2 +x_3^2$. Poskol'ku s kazhdym takim preobrazovaniem mozhno otozhdestvit' vrashenie, to legko videt', chto trehmernye vrasheniya obrazuyut podgruppu preobrazovanii Lorenca.

Napishem matricu povorota s uchetom chetvertoi koordinaty:


\begin{displaymath} \hat \Omega= \left( \begin{array}{llll} \omega_{11} & \omega... ... & \omega_{33} & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} \right) \end{displaymath} (2.19)

Zdes' v kachestve elementov matricy chetyrehmernyh povorotov $\hat \Omega$ ispol'zovany elementy matricy trehmernyh povorotov $\hat \omega$.

Rassmotrim teper' chetyrehmernye lineinye preobrazovaniya tipa (2.16). Otmetim, chto takie lineinye preobrazovaniya yavlyayutsya preobrazovaniyami tipa vrasheniya, no ne preobrazovaniyami tipa sdviga. Dlya nachala naidem preobrazovanie svyazannoe s vrasheniem vremennoi koordinaty.

Preobrazovaniya svyazannye s preobrazovaniyami Lorenca vklyuchayushimi vremennuyu koordinatu, no isklyuchayushie vrasheniya prostranstvennyh koordinat matematiki nazyvayut preobrazovaniyami giperbolicheskogo povorota, a fiziki bustami, t.e. preobrazovaniyami menyayushimi skorost' sistemy koordinat.

Rassmotrim preobrazovanie v ploskosti $(x_3, x_0)$. Takoe preobrazovanie ne dolzhno menyat' formu $x_0^2 -x_3^2$. Imenno eto preobrazovanie matematiki nazyvayut inogda giperbolicheskim povorotom. Matricu giperbolicheskogo povorota mozhno zapisat' analogichno matricam obychnogo povorota, zameniv trigonometricheskoe kosinus i sinus na giperbolicheskie kosinus i sinus:


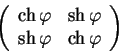
\begin{displaymath} \left( \begin{array}{ccc} \ch \varphi & \sh \varphi \\ \sh \varphi & \ch \varphi \\ \end{array}\right) \end{displaymath}

V chetyrehmernom vide eta matrica budet imet' vid


\begin{displaymath} \hat \Omega_{03}= \left( \begin{array}{llll} 1 & 0 & 0 & 0 ... ...\ 0 & 0 & \sh \varphi & \ch \varphi \\ \end{array} \right) \end{displaymath} (2.20)

Podobnym zhe obrazom budut vyglyadet' matricy, kotorye opisyvayut povoroty v ploskostyah $(x_1, x_0)$, $(x_2, x_0)$. Matricu slozhnogo povorota, opisyvaemuyu kak trigonometricheskimi funkciyami, tak i vklyuchayushuyu giperbolicheskii povorot, opisyvaemyi giperbolicheskimi funkciyami mozhno poluchit' pol'zuyas' teoremami slozheniya trigonometricheskih i giperbolicheskih funkcii.

Tem ne menee v astronomii proshe ispol'zovat' preobrazovaniya Lorenca naidennye v drugom vide, kotoryi my seichas obsudim.

Rassmotrim vnov' obshie preobrazovaniya Lorenca vida (2.16), no zapisannye dlya differencialov koordinat. Pust' sistema $\Xi$ pokoitsya otnositel'no nablyudatelya, a sistema $K$ dvizhetsya otnositel'no nego s proizvol'noi skorost'yu $\vec v$.

Preobrazovaniya opisyvayutsya uravneniem:

\begin{displaymath} d\hat x^{\alpha}=\sum_{\beta} \Omega^{\alpha}_{ \beta} d\xi_{\beta}, \end{displaymath} (2.21)

U nablyudatelya soputstvuyushego sisteme $\Xi$ menyaetsya tol'ko vremya, kotoroe yavlyaetsya sobstvennym vremenem etogo nablyudatelya. Differencialy prostranstvennyh koordinat etogo nablyudatelya v sisteme $\Xi$ ravny nulyu, poskol'ku koordinaty neizmenny. Poetomu vektor opisyvayushii izmenenie differencialov nablyudatelya est' $(d\tau, 0, 0, 0)$. V sisteme $K$ differencialy nablyudatelya est':

$\displaystyle d\hat x^i= \Lambda^i_0 d\tau,$ (2.22)
$\displaystyle \qquad$ (2.23)
$\displaystyle d t = \Lambda^0_0 d \tau . \nonumber$  

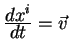Otnoshenie ${\displaystyle d x^i\over\displaystyle d t}=\vec v$ opredelyaet skorost' dvizheniya koordinatnyh sistem drug otnositel'no druga. Poetomu mozhno zapisat' ravenstvo:

\begin{displaymath} \Lambda^i_0= {\displaystyle v^i\over\displaystyle c} \Lambda^0_0 \end{displaymath} (2.24)

Napomnim, chto $x^0=ct$. Vyvedem vtoroe uravnenie dlya svyazi $\Lambda^i_0$ i $\Lambda^0_0$. Dlya etogo vychislim interval mezhdu sobytiyami razdelyaemymi differencialami $d\xi^{\alpha}$ v sisteme $\Xi$ i differencialami $d x^{\alpha}$ v sisteme $K$. Togda mozhno zapisat' uravnenie vida:

\begin{displaymath} \sum_{\alpha \beta} \eta_{\alpha \beta} d x^{\alpha} d x^{\b... ...eta} \eta_{\alpha \beta} \Lambda^{\alpha}_0 \Lambda^{\beta}_0 \end{displaymath} (2.25)

Otsyuda legko naiti (poskol'ku v sisteme soputstvuyushei nablyudatelyu spravedlivo ravenstvo $ds^2=c^2d\tau^2$), chto:

\begin{displaymath} 1 +\sum_i (\Lambda^i_0)^2 = (\Lambda^0_0)^2 \end{displaymath} (2.26)

Teper' podstavlyaem v uravnenie (2.26) uravnenie opredelyayushie razlichnye elementy matricy busta cherez skorosti (2.24) i poluchaem uravneniya dlya opredeleniya elementov matricy $\hat \Omega$:

$\displaystyle \Lambda^0_0=\gamma,$ (2.27)
$\displaystyle \vphantom{\Omega^0_0=\gamma}$  
$\displaystyle \Lambda^i_0={\displaystyle v^i\over\displaystyle c} \gamma,$  

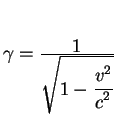gde $\gamma={\displaystyle 1\over\displaystyle\sqrt{1-{\displaystyle v^2\over\displaystyle c^2}}}$.

Uravneniya (2.25, 2.26) yavlyayutsya sledstviem bolee obshego uravneniya:

\begin{displaymath} \eta_{\mu \nu}=\sum_{\alpha \beta} \Lambda^{\alpha}_{\mu} \Lambda^{\beta}_{\nu} \eta_{\alpha \beta} \end{displaymath} (2.28)

Pol'zuyas' etim uravnenie mozhno naiti elementy matricy $\hat \Omega$ s dvumya prostranstvennymi indeksami. Sleduet, odnako, srazu skazat', chto elementy etoi matricy opredelyayutsya neodnoznachno. Oni vsegda mogut byt' umnozheny na matricu trehmernogo vrasheniya.

Vyberem vid trehmernyh elementov chetyrehmernoi matricy vrasheniya kak:

\begin{displaymath} \Lambda^i_j=\delta^i_j -v^i v_j {\displaystyle\gamma -1\over\displaystyle v^2} \end{displaymath} (2.29)

Zametim, chto vektornye komponenty s nizhnimi indeksami otlichayutsya znakom ot vektornyh komponent s verhnimi indeksami $v_j=\eta_{j i}v^i$.

Proizvol'noe preobrazovanie Lorenca mozhet byt' vyrazheno kak proizvedenie trehmernogo vrasheniya s bustom, kotoryi opisyvaetsya matricei $\Lambda^{\mu}_{\nu}$. Dokazatel'stvo etogo utverzhdeniya vyhodit za ramki kursa, no chitatel', znakomyi s teoriei grupp legko vosproizvedet ego. Predstavim proizvol'noe preobrazovanie Lorenca v vide:

\begin{displaymath} \Omega^{\mu}_{\nu}=\Lambda^{\mu}_{\alpha}\omega^{\alpha}_{\nu} \end{displaymath} (2.30)

V takom vide preobrazovaniya Lorenca legko primenyat' dlya polucheniya uravnenii redukcii.

2.3 Preobrazovaniya vektorov

Iz kursa lineinoi algebry izvestno, chto pri preobrazovaniyah vida (2.21) vektora preobrazuyutsya kak

\begin{displaymath} A^{\mu}=\Omega^{\mu}_{\nu} A^{\nu} \end{displaymath} (2.31)

Krome etogo, obshego, uravneniya mozhno takzhe privesti eshe neskol'ko uravnenii, kotorye yavlyayutsya ochen' poleznymi pri vyvode uravnenii redukcii, hotya oni obladayut men'shei obshnost'yu, chem (2.31). Odnim iz takih uranenii yavlyaetsya skalyarnoe proizvedenie vektorov. Skalyarnoe proizvedenie dvuh vektorov:

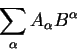
\begin{displaymath} \sum_{\alpha} A_{\alpha}B^{\alpha} \end{displaymath}

yavlyaetsya invariantom koordinatnyh preobrazovanii. Dokazhem eto dlya lineinyh preobrazovanii vida (2.21). Pust' vektora $A_{\alpha}$ i $B^{\alpha}$ zadany v sisteme $\Xi$, sdelaem preobrazovanie vida (2.21) k novoi sisteme koordinat $K$, kotoraya dvizhetsya so skorost'yu $\vec v$ otnositel'no sistemy $\Xi$, krome togo, osi sistemy $K$ povernuty otnositel'no pervoi sistemy v proizvol'nom napravlenii, kotoroe harakterizuetsya tremya uglami Eilera. Teper' vychislim komponenty vektorov $A_{\alpha}$ i $B^{\alpha}$ v novoi sisteme $K$:

\begin{displaymath} \hat A_{\mu}=\Omega_{\mu}^{\alpha} A_{\alpha}, \end{displaymath}

i


\begin{displaymath} \hat B^{\mu}=\Omega^{\mu}_{\alpha} B^{\alpha} \end{displaymath}

Skalyarnoe proizvedenie vektorov v sisteme $K$ vyrazhaetsya cherez proizvedenie vektorov v sisteme $\Xi$ s matricami preobrazovaniya:

\begin{displaymath} \hat A_{\alpha} \hat B^{\alpha}= \Omega_{\alpha}^{\beta}\Omega_{\gamma}^{\alpha} A_{\beta} B^{\gamma} \end{displaymath}

Pryamym vychislenie proizvedeniya maric mozhno pokazat', chto

\begin{displaymath} \Omega_{\alpha}^{\beta}\Omega_{\gamma}^{\alpha} =\delta^{\beta}_{\gamma} \end{displaymath} (2.32)

Zdes' $\delta^{\alpha}_{\beta}$ - simvol Kronekera ili edinichnaya matrica2.2:


\begin{displaymath} \delta^{\alpha}_{\beta}= \left( \begin{array}{cccc} 1& 0& 0&... ...& 1& 0& 0 \\ 0& 0& 1& 0 \\ 0& 0& 0& 1 \\ \end{array}\right) \end{displaymath} (2.33)

Podstavim (2.33) v (2.32) i polchim, chto skalyarnoe proizvedenie vektorov v dvuh sistemah koordinat ravno drug drugu. Eto i oznachaet, chto skalyarnoe proizvedenie yavlyaetsya invariantom pri preobrazovaniyah Lorenca. Zametim srazu, chto skalyarnoe proizvedenie yavlyaetsya invariantnym pri lyubyh, dazhe nelineinyh preobrazovaniyah. Dokazatel'stvo etogo utverzhdeniya otlozhim do pyatoi lekcii.

Krome vektorov nam inogda pridetsya proizvodit vychisleniya s ob'ektami bolee slozhnoi prirody - tenzorami i tenzornymi plotnostyami.

Tenzor vtorogo ranga ekvivalenten chetyrehmernoi kvadratnoi matrice $A^{\alpha \beta}$. Etot tenzor preobrazuetsya soglasno pravilu:

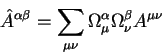
\begin{displaymath} \hat A^{\alpha \beta} =\sum_{\mu \nu} \Omega^{\alpha}_{\mu} \Omega^{\beta}_{\nu} A^{\mu \nu} \end{displaymath}

v sluchae, kogda nado preobrazovat' tenzory vtorogo ranga s dvumya nizhnimi indeksami ili s odnim verhnim i odnim nizhnem indeksami neobhodimosummirovat' ih s $\hat \Omega$ matricami s dvumya verhnimi indeksami summirovaniya ili so smeshannymi indeksami summirovaniya.

Tenzory bolee vysokogo ranga pri preobrazovaniyah soderzhat' bol'she proizvedenii matric $\hat \Omega$. tenzory tret'ego ranga tri matricy, tenzory chetvertogo ranga - chetyre i t.p.

2.4 Chetyrehmernaya skorost'

Kinematicheskie i dinamicheskie velichiny v chetyrehmernom prostranstve otlichayutsya ot sootvetstvuyushih trehmernyh velichin. Vnachale opredelim chetyrehmernuyu skorost'.

Obychnaya trehmernaya skorost' opredelyaetsya kak otnoshenie proidennogo puti na promezhutok vremeni, za kotoryi etot put' proiden:

\begin{displaymath} \vec v={\displaystyle d \vec r\over\displaystyle dt} \end{displaymath}

Iz etoi formuly vidno, chto dlya opredeleniya skorosti v trehmernom prostranstve ispol'zuetsya vneshnii po otnosheniyu trehmernomu prostranstvu parametr - vremya. Esli my postroim traektoriyu probnoi chasticy v trehmernom prostranstve v vide treh funkcii vremeni, kotorye est':


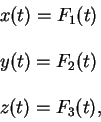
\begin{displaymath} \begin{array}{l} x(t)=F_1(t)\\ \qquad\\ y(t)=F_2(t)\\ \qquad\\ z(t)=F_3(t), \end{array}\end{displaymath}

to skorost' mozhno opredelit' takzhe kak kasatel'nyi vektor

\begin{displaymath} \vec v =({\displaystyle d x(t)\over\displaystyle dt}, {\disp... ...displaystyle dt}, {\displaystyle d z(t)\over\displaystyle dt}) \end{displaymath}

k etoi traektorii.

Po analogii s etim opredeleniem opredelyayut chetyrehmernuyu skorost' kak vektor, kasatel'nyi k chetyrehmernoi traektorii chasticy. V kachestve parametra vdol' traektorii vybirayut nekotoryi afinnyi parametr. Dlya chastic, kotorye obladayut massoi i dvizhutsya so skorost'yu men'she chem skorost' sveta v kachestve afinnogo parametra vdol' traektorii obychno vybirayut interval:


\begin{displaymath} u^{\mu}={\displaystyle d x^{\mu}\over\displaystyle d s} \end{displaymath} (2.34)

Otmetim vazhnoe otlichie chetyrehmernoi skorosti, opredelennoi soglasno (2.34) ot trehmernoi skorosti. Absolyutnaya velichina trehmernoi skorosti yavlyaetsya proizvol'noi velichinoi. Absolyutnaya velichina chetyrehmernoi skorosti ravna edinice.

\begin{displaymath} \sum_{\alpha} u^{\alpha} u_{\alpha}=1 \end{displaymath} (2.35)

V sluchae, kogda my rassmatrivaem probnuyu chasticu, kotoraya dvizhetsya so skorost'yu sveta (naprimer, foton), to v kachestve parametra vdol' traektorii vybirayut drugoi afinnyi parametr, naprimer, put', proidennyi fotonom. Chetyrehmernyi interval vdol' traektorii chasticy dvizhusheisya so skorost'yu sveta uzhe vybirat' nel'zya, poskol'ku on raven nulyu.

Privedem yavnyi vid chetyrehmernoi skorosti cherez trehmernuyu:

\begin{displaymath} u^{\mu} =\left( \gamma, \gamma {\displaystyle\vec v\over\displaystyle c}\right) \end{displaymath} (2.36)

Privedem takzhe uravnenie dlya redukcii volnovogo vektora fotona k nablyudatelyu. Dlya etogo vospol'zuemsya tem svoistvom, chto vektornoe proizvedenie volnovogo vektora fotona $k^{\mu}$ i chetyrehmernoi skorosti nablyudatelya yavlyaetsya invariantnoi velichinoi

\begin{displaymath} \sum_{\alpha} k_{\alpha} u^{\alpha} =const \end{displaymath} (2.37)

Invariantnost' otnositel'no preobrazovaniya sistemy koordinat oznachaet, chto $const$ ne menyaet svoego znacheniya pri perehode ot, skazhem, pokoyusheisya sistemy koordinat, k dvizhusheisya. Rassmotrim nekotorogo nablyudatelya $O$ i ego chetyrehmernuyu skorost' $u^{\alpha}_O$. V sisteme koordinat soputstvuyushei nablyudatelyu vektor skorosti prinimaet znachenie

\begin{displaymath} u^{\alpha}_O = (1, 0, 0, 0) \end{displaymath}

Sootvetstvenno skalrnoe proizvedenie dvuh chetyrehmernyh vektorov vyrozhdaetsya v proizvedenie dvuh velichin: nulevoi komponenty volnovogo vektora fotona i nulevoi komponenty chetyrehmernoi skorosti. Poskol'ku vtoroi somnozhitel' raven edinice, to ostaetsya tol'ko odna velichina $k_0$ komponenta volnovogo vektora fotona. Eta komponenta otozhdestvlyaetsya s nablyudaemoi chastotoi fotona (ili s energiei fotona v sisteme koordinat, soputstvuyushei nablyudatelyu) $\nu_O$. Takim obrazom opredelyaetsya znachenie $const$, kotoraya stoit v pravoi chasti uravneniya (2.37).

Znachenie konstanty v pravoi storone ravenstva (2.37), razumeetsya, budet drugim dlya drugogo ob'ekta. Rassmotrim v kachestve drugogo tela istochnik fotonov. Vychislim pravuyu chast' (2.37) v sisteme koordinat, kotoraya soputstvuet istochniku. Teper' konstanta v pravoi storone ravenstva budet opredelyat' chastotu izlucheniya $\nu_E$. Estestvenno, chto velichina konstanty budet uzhe drugaya.

Costavim teper' otnoshenie dvuh velichin. Chislitel' etogo otnosheniya - proizvedenie chetyrehmernoi skorosti istochnika fotonov na volnovoi vektor fotona. Znamenatelem yavlyaetsya skalyarnoe proizvedenie chetyrehmernoi skorosti nablyudatelya v sisteme koordinat emu soputstvuyushei.

\begin{displaymath} 1+z={\displaystyle\sum_{\alpha} k_{\alpha} u^{\alpha}\vert _... ...er\displaystyle\sum_{\alpha} k_{\alpha} u^{\alpha}\vert _O } \end{displaymath} (2.38)

Zdes' indeks $O$ oznachaet "nablyudatel'", a indeks $E$ oznachaet "izluchatel'". Velichina $z$ obychno nazyvaetsya krasnym smesheniem, ona prishla v relyativistskuyu teoriyu iz kosmologii, v kosmologii eto odin iz osnovnyh parametrov, kotoryi harakterizuet istochnik.

Poskol'ku sprava stoit otnoshenie dvuh konstant, kotorye my uzhe vychislili, to napishem eto otnoshenie yavno:

\begin{displaymath} {\displaystyle\nu_E\over\displaystyle\nu_O} = 1 +z \end{displaymath} (2.39)

Teper' dlya togo, chtoby vychislit' chastotu fotona, kotoruyu budet izmeryat' nablyudatel', postupim sledushim obrazom. V sisteme koordinat, soputsvuyushei nablyudatelyu, volnovoi vektor fotona imeet komponenty


\begin{displaymath} k_{\mu}= 2 \pi \nu_O\left(1, \vec n \right), \end{displaymath}

zdes' $\vec n$ -vektor v napravlenii izlucheniya fotona. Vse velichiny vychisleny v sisteme koordinat soputstvuyushei nablyudatelyu.

Izluchatel' imeet chetyrehmernuyu skorost'

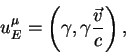
\begin{displaymath} u^{\mu}_E =\left( \gamma, \gamma {\displaystyle\vec v\over\displaystyle c}\right) , \end{displaymath}

gde $\vec v$ -trehmernaya skorost' istochnika fotonov otnositel'no nablyudatelya.

Skalyarnoe proizvedenie v sisteme koordinat nablyudatelya est'

\begin{displaymath} \sum_{\alpha} k_{\alpha} u^{\alpha}=2 \pi \nu_O \gamma \left( 1 +{\displaystyle(\vec n \vec v)\over\displaystyle c}\right) \end{displaymath} (2.40)

Teper' poluchaem, chto otnoshenie chastoty izluchatelya k chastote togo zhe fotona v sisteme nablyudatelya est':

\begin{displaymath} {\displaystyle\nu_E\over\displaystyle\nu_O} = \gamma \left( 1 +{\displaystyle(\vec n \vec v)\over\displaystyle c}\right) \end{displaymath} (2.41)

Eto est' zakon Dopplera v special'noi teorii otnositel'nosti.

Rassmotrim uravnenie (2.41) bolee podrobno.

Budem schitat', chto istochnik fotonov i nablyudatel' nahodyatsya na osi $Ox$ i istochnik dvizhetsya vdol' etoi osi. Pust' izluchatel' dvizhetsya po napravleniyu k nablyudatelyu. Togda $(\vec n \vec v)= -v$ i nablyudaemaya chastoty bol'she chastoty izluchatelya:

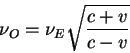
\begin{displaymath} \nu_O = \nu_E \sqrt{{\displaystyle c + v\over\displaystyle c - v}} \end{displaymath}

Chastota fotonov smeshaetsya v golubuyu storonu spektra, my imeem delo s golubym smesheniem.

V tom sluchae, kogda napravlenie rasprostraneniya fotonov protivopolozhno dvizheniyu istochnika $(\vec n \vec v) = v$ voznikaet effekt krasnogo smesheniya chastoty:

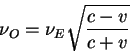
\begin{displaymath} \nu_O = \nu_E \sqrt{{\displaystyle c - v\over\displaystyle c + v}} \end{displaymath}

Rassmotrim eshe odin lyubopytnyi primer. A imenno, pod kakim uglom k napravleniyu rasprostraneniya fotonov dolzhen dvigat'sya istochnik, chtoby smeshenie chastoty otsutstvovalo? Itak, na yazyke matematiki etu zadachu mozhno sformulirovat' sledushim obrazom: Naiti takoe znachenie 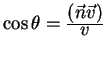$\cos \theta = {\displaystyle(\vec n \vec v)\over\displaystyle v}$ pri uslovii $v \ne 0$, dlya kotorogo $\nu_O = \nu_E$.

Iz usloviya ravenstva chastot poluchaem, chto kosinus ugla mezhdu napravleniem dvizheniya istochnika fotonov i napravleniem na nablyudatelya est':

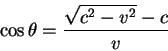
\begin{displaymath} \cos \theta = {\displaystyle\sqrt{c^2 - v^2} - c\over\displaystyle v} \end{displaymath}

Iz privedennogo uravneniya vidno, chto effekt smesheniya chastoty mozhet otsutstvovat' lish' dlya istochnika udalyayushegosya ot nablyudatelya.

Uravnenie (2.41) opisyvaet izmenenie chastoty pri perehode ot dvizhushegosya istochnika k nepodvizhnomu nablyudatelyu. V real'nosti obychno istochnik fotonov i nablyudatelya razdelyaet nekotoroe rasstoyanie. Izmenenie chastoty fotona pri raprostranenii formula (2.41) ne opisyvaet. Esli v prostranstve mezhdu istochnikom fotonov i nablyudatelem prisutstvuet, naprimer, gravitacionnoe pole, to poyavlyaetsya dopolnitel'noe izmenenie chastoty, kotoroe dolzhno byt' uchteno.


<< 1. Principy otnositel'nosti | Oglavlenie | 3. Uskorennye sistemy otscheta >>

Publikacii s klyuchevymi slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni
Publikacii so slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mneniya chitatelei [21]
Ocenka: 3.1 [golosov: 132]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya