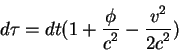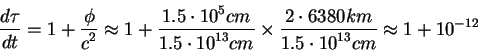Astronet > 3. Uskorennye sistemy otscheta i STO

po tekstam po klyuchevym slovam v glossarii po saitam perevod po katalogu

Teoriya otnositel'nosti dlya astronomov

<< 2. Special'naya teoriya otnositel'nosti | Oglavlenie | 4. Eksperimenty po OTO >>

Razdely

3.1 Vklyuchenie gravitacii v STO.

3. Uskorennye sistemy otscheta i STO

Uspeh special'noi teorii otnositel'nosti, pravil'noe formulirovanie principa otnositel'nosti dlya inercial'nyh sistem otscheta dvizhushihsya so skorostyami blizkimi k skorosti sveta pobudil A.Einshteina na rasprostranenie etogo principa na uskorennye sistemy otscheta.

Teper' vkratce rasskazhem kak A.Einshtein smog opisat' uskorennye sistemy otscheta v terminah principa otnositel'nosti, kak stalo ponyatno, chto eto opisanie privodit k geometricheskoi traktovke gravitacionnogo polya, neobhodimosti vvedeniya neevklidovoi geometrii v fiziku i idei iskrivlennogo prostranstva - vremeni. Osnovnaya ideya stala ponyatnoi A.Einshteinu v 1907 g., hotya v original'nom vide ona byla opublikovana tol'ko v 1972 g. v gazete "New York Times". Eto ideya pozzhe poluchila nazvanie relyativistskogo principa ekvivalentnosti Einshteina. Sam A.Einshtein opisal to vremya i mysli v otryvke, kotoryi pomeshen nizhe. Perevod etogo na russkii yazyk slishkom krasiv, chtoby ego opustit':

" Ya pytalsya modificirovat' teoriyu gravitacii N'yutona takim obrazom, chtoby ona tochno sootvetstvovala special'noi teorii otnositel'nosti. Popytki sdelat' eto pokazali, chto teoriya gravitacii mozhet byt' soglasovana s principami special'noi teorii otnositel'nosti, no oni ne udovletvoryali menya, poskol'ku trebovali vvedeniya gipotez ne soderzhashih fizicheskih osnov. V eto vremya ko mne prishla schastliveishaya ideya moei zhizni ^3.1 v sledushem vide:
Tochno takzhe, kak elektricheskoe pole sozdaetsya elektromagnitnoi indukciei, gravitacionoe pole mozhet sushestvovat' tol'ko otnositel'no. Sledovatel'no, dlya nablyudatelya, nahodyashegosya v svobodnom padenii s kryshi doma, gravitacionnogo polya ne sushestvuet ( po krainei mere v beskonechno blizkoi ego okrestnosti ) v techenii vsego vremeni padeniya. Esli nablyudatel' vypustit iz ruk kakie - libo predmety oni ostanut'sya otnositel'no etogo nablyudatelya v sostoyanii pokoya nezavisimo ot ih himicheskogo sostava ili fizicheskogo sostoyaniya ^3.2. Nablyudatel' v etom sluchae dolzhen priznat', chto on nahoditsya v sostoyanii pokoya.

Chrezvychaino interesnyi empiricheskii zakon glasyashii, chto vse tela v odnom i tom zhe gravitacionnom pole padayut s odnim i tem zhe uskoreniem, poluchal v etom sluchae glubokii fizicheskii smysl. Esli by nashelsya hotya by odin predmet, kotoryi padal by v gravitacionnom pole ne tak kak drugie, to nablyudatel' sravnivaya svoe dvizhenie s dvizheniem etogo predmeta smog by skazat', chto on nahoditsya v gravitacionnom pole i chto on padaet pod ego vozdeistviem. No esli takogo predmeta ne sushestvuet, a eksperiment podtverzhdaet etot fakt s bol'shoi stepen'yu tochnosti, nablyudatel' teryaet vsyakoe ob'ektivnoe osnovanie rassmatrivat'sya svoe sostoyanie kak sostoyanie padeniya v gravitacionnom pole. Skoree on imeet pravo rassmatrivat' svoe sostoyanie kak sostoyanie pokoya i schitat', chto v ego blizhaishem okruzhenii gravitacionnoe pole otsutstvuet.

Takim obrazom, izvestnyi eksperimental'nyi fakt, chto uskorenie v gravitacionnom pole ne zavisit ot himicheskogo sostava ili fizicheskogo sostoyaniya stanovitsya moguchim argumentom dlya rasprostraneniya principa otnositel'nosti na koordinatnye sistemy, kotorye dvizhutsya neravnomerno odna otnositel'no drugoi."

3.1 Vklyuchenie gravitacii v STO.

Risunok 3.1: Na risunke izobrazhen lift, v kotorom uskorenie modeliruet pole tyazhesti.

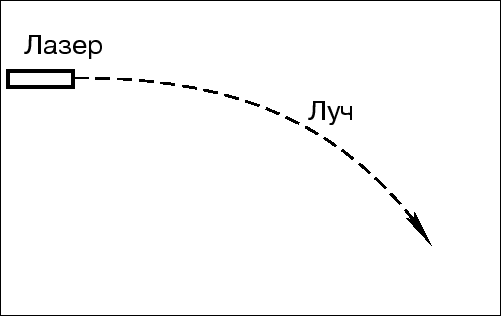
$\begin{figure}\centerline{\epsfxsize=0.7\textwidth\epsfbox{fig3_1.ai}}\end{figure}$

Rassmotrim na ris. 3.1 poyasneniya k principu ekvivalentnosti Einshteina, kotoryi rasprostranyaet princip otnositel'nosti na uskorennye sistemy koordinat.

Na levom risunke izobrazhen lift, uskoryaemyi vverh s velichinoi uskoreniya ravnoi . Svet, izobrazhennyi na risunke punktrinoi liniei dvizhetsya v takom lifte po iskrivlennoi traektorii. Eta iskrivlennaya traektoriya yavlyaetsya ideal'no pryamoi liniei, no v pokoyasheisya sisteme otscheta. V uskorennoi sisteme otscheta liniya stanovitsya iskrivlennoi. Na pravom risunke izobrazhen tot zhe samyi lift, kotoryi nahoditsya v pole tyazhesti s odnorodnym uskoreniem. Princip otnositel'nosti primenennyi k uskorennym sistemam otscheta glasit, chto nevozmozhno otlichit' dve etih situacii. Znachit, v lifte, kotoryi nahoditsya v gravitacionnom pole svet tozhe dolzhen dvigatsya po iskrivlennoi traektorii.

Vychislim harakteristiki sveta pri dvizhenii v odnorodnom pole tyazhesti pol'zuyas' harakteristikami sveta v uskorennom lifte. Dlya etogo rassmotrim fotony, kotorye rasprostranyayutsya vdol' polya tyazhesti $\vec g$ . Eto gravitacionnoe pole ishodya iz principa ekvivalentnosti mozhno zamenit' polem uskoreniya s ravnoi velichinoi, no protivopolozhnym znakom. Rassmotrim lazer , kotoryi izluchaet fotony s chastotoi $\nu_0$ (eta chastota izmeryaetsya nablyudatelem, nahodyashimsya ryadom s lazerom, t.e. soputstvuyushego lazeru). Na rasstoyanii ot lazera (po napravlenniyu dvizheniya) nahoditsya drugoi nablyudatel' , kotoryi tozhe izmeryaet parametry sveta. 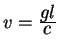Svet, kotoryi vyshel iz lazera v moment vremeni dostignet nablyudatelya v moment vremeni $t={\displaystyle l\over\displaystyle c}$ , a sam nablyudatel' budet imet' skorost' otnositel'no lazera ravnuyu $v={\displaystyle gl\over\displaystyle c}$ .

Rassmotrim teper' dve dopolnitel'nye inercial'nye sistemy koordinat, kotorye dvigayutsya ravnomerno i pryamolineino, tak chto uskorenie v etih sistemah ravno nulyu. V pervoi sisteme koordinat v nachale sistemy nahoditsya nablyudatel' . Skorost' i polozhenie etoi sistemy vybrany tak, chtoby v moment vrmeni nablyudatel' nahodilsya v beskonechno maloi okrestnosti tochki uskorennoi sistemy koordinat. Vtoraya inercial'naya sistema dvizhetsya so skorost'yu otnositel'no pervoi tak, chtoby v moment vremeni $t={\displaystyle l\over\displaystyle c}$ ee nachalo, v kotorom nahorditsya nablyudatel' sovpalo s polozheniem nablyudatelya , nahodyashegosya v uskorennoi sisteme koordinat.

Privlechenie dopolnitel'nyh inercial'nyh sistem koordinat sdelano ne dlya togo, chtoby zaputat' studenta, a dlya togo, chtoby provesti raschety harakteristik sveta pol'zuyas' uzhe znakomymi formulami special'noi teorii otnositel'nosti.

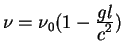
Chastota fotona izmerennaya nablyudatelem v moment vremeni est' $\nu_0$ , soglasno nashemu opredeleniyu. V moment vremeni chastota togo zhe fotona, izmerennaya nablyudatelem , dvizhushemsya so skorost'yu otnositel'no est' $\nu=\nu_0(1-{\displaystyle gl\over\displaystyle c^2})$

Lazer predstavlyaet iz sebya standartnyi elektromagnitnyi oscillyator s sobstvennoli chastotoi $\nu_0$ i s periodom $P_0={\displaystyle 1\over\displaystyle\nu_0}$ . Sootvetstvenno, nablyudatel' budet izmeryat' period oscillyatora:

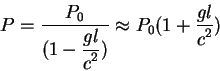
$\begin{displaymath} P={\displaystyle P_0\over\displaystyle(1-{\displaystyle gl\o... ...^2})} \approx P_0(1+ {\displaystyle gl\over\displaystyle c^2}) \end{displaymath}$

Proizvedenie uskoreniya na rasstoyanie predstavlyaet raznost' gravitacionnyh potencialov mezhdu dvumya tochkami. V pervoi tochke nahoditsya lazer, vo vtoroi nahaoditsya nablyudatel': $\phi=gl$ . Teper' mozhno privesti formulu opredelyayushuyu temp techeniya vremeni v dvuh tochkah i :

$\begin{displaymath} \tau=t(1 +{\displaystyle\phi\over\displaystyle c^2}) \end{displaymath}$

(3.1)

Podstavim etu formulu v uravnenie dlya chetyrehmernogo intervala. Poskol'ku (3.1) predstavlyaet svyaz' sobstvennogo vremeni tochki , t.e. $\tau$ s koordinatnym vremenem (kotoroe my otnosim k sobstvennomu vremeni tochki , v kotoroi potencial nulevoi), to mozhno zapisat' chetyrehmernyi interval kak funkciyu sobstvennogo vremeni i kak funkciyu koordinatnogo vremeni:

$\begin{displaymath} ds^2=c^2 d\tau^2=(1 +{\displaystyle 2\phi\over\displaystyle c^2})\times c^2\; dt^2 \end{displaymath}$

(3.2)

Osnovnoe izmenenie po sravneniyu s prezhnei velichinoi, kotoraya harakterizovala "rasstoyanie" mezhdu sobytiyami v STO - poyavlenie koefficenta pered kvadratom differenciala vremeni. Etot koefficent, voobshe govorya, yavlyaetsya funkciei vseh chetyreh koordinat. Takie funkcii poyavlyayutsya v tom sluchae, kogda metrika yavlyaetsya neevklidovoi, a geometriya opisyvaet iskrivlennoe prostranstvo - vremya. Poetomu novaya fizika - opisanie sil'nyh gravitacionnyh polei - harakterizuetsya neevklidovoi geometriei. Dlya raboty v obshei teorii otnositel'nosti neobhodimo vladet' apparatom neevklidovoi geometrii, kotoraya budet izlagat'sya pozzhe v etom kurse.

Vernemsya k formule (3.2). V tom sluchae, kogda nablyudatel' dvizhetsya v pole $\phi$ so skorost'yu , to ego sobstvennoe vremya $\tau$ svyazano s koordinatnym vremenem kak:

$\begin{displaymath} d\tau=dt(1 +{\displaystyle\phi\over\displaystyle c^2} -{\displaystyle v^2\over\displaystyle 2c^2}) \end{displaymath}$

(3.3)

Dlya togo, chtoby ocenit' skorost' techeniya vremeni v gravitacionnom potenciale razlichnoi velichiny provedem raschet na skol'ko "uhodyat" drug otnositel'no druga chasy, nahodyashiesya na poludennoi i polunochnoi storone Zemli v gravitacionnom pole Solnca. Budem schitat', chto chlen proporcional'nyi kvadratu skorosti nablyudatelei razlichaetsya dlya dvuh nablyudatelei na prenebrezhimo maluyu velichinu. Ocenivat' raznost' skorosti techeniya vremeni budem tol'ko po formule (3.3).

$\begin{displaymath} {\displaystyle d\tau\over\displaystyle dt}=1 +{\displaystyle... ...m\over\displaystyle 1.5 \cdot 10^{13} cm}\approx 1 +10^{-12} \end{displaymath}$

(3.4)

Eto znachit, chto, skazhem, za 12 chasov dvoe chasov "razoidutsya" na vremya ravnoe $\sim$ 220 nanosekund. Eto vpolne obnaruzhimoe, a dlya nekotoryh processov dazhe bol'shoe vremya. B $\grave o$ l'shee vremya pokazhut chasy, kotorye raspolozheny dal'she ot Solnca - chasy na polunochnoi storone Zemli. Na ris. 3.1 pokazan grafik skorosti hoda chasov v zavisimosti ot rasstoyaniya ot baricentra Solnca. Vot tol'ko dlya obnaruzheniya etoi raznicy v skorosti techeniya vremeni neobhodimo nahodit'sya daleko ot Zemli, naprimer, na Solnce.

Tem ne menee izmerit' podobnyi effekt mozhno takzhe i na Zemle i v blizhnem kosmose. Rassmotrim dva interesnyh effekta - izmenenie skorosti hoda chasov v zavisimosti ot sezona i izmenenie skorosti hoda chasov ustanovlennyh na sputnike sistemy GPS po sravneniyu s chasami ustanovlennymi na Zemle.

Os' vrasheniya Zemli naklonena po otnosheniyu k ploskosti zemnoi orbity na ugol $\sim 23^{\circ}.5$ . Poetomu chasy, skazhem 1 i 2 s sobstvennym vremenem $\tau_1$ i $\tau_2$ , kotorye nahodyatsya na raznyh shirotah, sootvetstvenno $\varphi_1$ i $\varphi_2$ , nahodyatsya takzhe pri raznyh znacheniyah gravitacionnogo potenciala Solnca. Estestvenno, chto pri dvizhenii Zemli po orbite voznikaet godovaya garmonika v izmenenii skorosti hoda chasov:

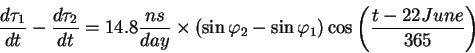
$\begin{displaymath} {\displaystyle d \tau_1\over\displaystyle d t} - {\displayst... ...t( {\displaystyle t - 22 June\over\displaystyle 365} \right) \end{displaymath}$

Zdes' v kachestve nachala otscheta vybran den' letnego solncestoyaniya. Na korotkih promezhutkah vremeni, znachitel'no men'shih dlitel'nosti goda takoe izmenenie skorosti techeniya vremeni vosprinimaetsya kak lineinyi dreif chasov, zavisyashii ot shiroty! Velichina etogo dreifa $\sim$ 15 nanosekund v den'. Takoi effekt deistvitel'no nablyudaetsya i priroda ego nikak neob'yasnima, esli "zabyt'" pro effekty obshei teorii otnositel'nosti.

Obshaya teoriya otnositel'nosti izmenila nashi vzglyady na strukturu prostranstva i vremeni. V techenii dolgogo vremeni OTO ostavalas' teoreticheskim instrumentom sovremennoi fiziki, kotoryi ne imeet prilozhenii v tehnologii. Situaciya sushestvenno izmenilas's poyavleniem vysokotochnoi navigacii, s poyavleniem sputnikovyh sistem GPS i GLONASS. Teper' dlya celei tochnoi navigacii (na poverhnosti Zemli) neobhodimo ispol'zovat' uravneniya obshei teorii otnositel'nosti dlya redukcii nablyudenii. Osobenno vazhno ispol'zovat' ih dlya perescheta standartov vremeni na Zemle i na sputnikah. Vysota poleta sputnikov prevyshaet zemnoi radius, a skorost' znachitel'no prevyshaet skorost' poleta sovremennyh samoletov. Poetomu izmenenie skorosti techeniya vremeni osobenno zametny. Sobstvennore vremya na bortu sputnika oboznachim $\tau_s$ , a na poverhnosti Zemli oboznachim $\tau_e$ . Otnoshenie dvuh intervalov sostavlyaet:

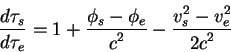
$\begin{displaymath} {\displaystyle d \tau_s\over\displaystyle d \tau_e} = 1 + {\... ...c^2} - {\displaystyle v_s^2 - v_e^2\over\displaystyle 2 c^2} \end{displaymath}$

Zdes' indeksy i sootvetstvenno otnosyatsya k potencialu Zemli na vysote poleta sputnika i skorosti ego poleta, a takzhe sootvetstvuyushie velichiny dlya standarta na Zemle.

Itak, skorost' techeniya vremeni na Zemle i na sputnike razlichna. Dlya sputnikov sistemy GPS, kotorye nahodyatsya na vysote 14 000 km otlichie dvuh tempov techeniya vremeni sostavlyaet 44 mikrosekundy v den'. Estestvenno, dlya podderzhaniya ravnomernoi shkaly vremeni, edinoi dlya poverhnosti Zemli i sputnikov neobhodimo uchityvat' eto izmenenie.

<< 2. Special'naya teoriya otnositel'nosti | Oglavlenie | 4. Eksperimenty po OTO >>

Publikacii s klyuchevymi slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni Publikacii so slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni
Sm. takzhe: 70 let Stivenu Hokingu Sputnik Gravity Probe B podtverdil nalichie gravimagnetizma Vsemirnyi god fiziki: triumf Einshteina Al'bert Einshtein opisyvaet prostranstvo-vremya Polnoe solnechnoe zatmenie Otdel pul'sarnoi astrometrii PRAO AKC FIAN O skorosti gravitacii - ot avtorov Vse publikacii na tu zhe temu >>

Mneniya chitatelei [21]

Versiya dlya pechati

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce