Rambler's Top100Astronet    
  po tekstam   po klyuchevym slovam   v glossarii   po saitam   perevod   po katalogu 		 

Na pervuyu stranicu
Teoriya otnositel'nosti dlya astronomov
<< 3. Uskorennye sistemy otscheta | Oglavlenie | 5. Neevklidova geometriya >>

Razdely

4. Eksperimenty po OTO

Naskol'ko vse teoreticheskie ocenki, kotorye obsuzhdalis' v predydushih glavah sootvetstvuyut deistvitel'nosti? Podtverzhdeny li eti formuly eksperimentom? Kak my uzhe pisali, special'naya teoriya otnositel'nosti ispol'zuetsya pri raschetah bol'shih mashin dlya fizicheskogo eksperimenta. Ispol'zovanie obshei teorii otnositel'nosti zaderzhalos'. Ee nachali primenyat' v tehnologii tol'ko poslednie dvadcat' let. Ispol'zovanie ee nachalos' s opredeleniya skorosti techeniya vremeni v gravitacionnom pole s razlichnym potencialom. Rasskazhem ob eksperimentah, kotorye polozhili nachalo primeneniyu obshei teorii otnositel'nosti v prikladnyh celyah.

4.1 Eksperimenty po proverke skorosti hoda vremeni

Pervyi eksperiment byl sdelan v 1971 g.[3]. Chetvero chasov sdelannyh na osnove cezievyh standartov chastoty byli pomesheny na dva samoleta i sovershili krugosvetnoe puteshestvie. Odni chasy puteshestvovali v vostochnom napravlenii, drugie obognuli Zemlyu v zapadnom napravlenii. Raznica v skorosti hoda vremeni voznikala iz-za dobavochnoi skorosti vrasheniya Zemli. Eto byl effekt, skoree special'noi teorii otnositel'nosti, chem obshei, odnako, chlen zavisyashii ot velichiny zemnogo potenciala v izmenenii skorosti hoda chasov takzhe prisutstvoval i vnes znachimyi vklad. Nado skazat', chto v pervom eksperimente bylo ochen' mnogo neopredelennostei svyazannyh s netochnost'yu izmereniya skorosti samoletov, vysotoi samoletov nad poverhnost'yu Zemli i ih polozheniem. Otsutstvoval takzhe vneshnii kontrol' hoda chasov i t.p. Tem ne menee, udalos' podtverdit' obshuyu teoriyu otnositel'nosti, udalos' izmerit' razlichie v skorosti hoda chasov na bortu dvuh samoletov. Teoreticheskie vychisleniya zaderzhki chasov byli:

Effekt Vostok Zapad
Potencial'nyi 144 $\pm$ 14 ns 179 $\pm$ 18 ns
chlen    
Dopplerovskii -184 $\pm$ 18 ns 96 $\pm$ 10 ns
chlen    
Polnaya -40 $\pm$ 23 ns 275 $\pm$ 21 ns
zaderzhka    

Eksperiment dal sledushii rezul'tat:

  Vostok Zapad
Polnaya -59 ns 273 ns
zaderzhka    

Prodemonstriruem na prostyh vykladkah, kak menyaetsya sobstvennoe vremya chasov, kotorye nahodyatsya na bortu dvuh samoletov, odin iz kotoryh letit na zapad, drugoi na vostok. Skorost' samoleta otnositel'no zemnoi poverhnosti oboznachim $\vec v_a$. Samolet dvigaetsya s poverhnosti vrashayusheisya Zemli, ego skorost' otnositel'no pokoyusheisya sistemy koordinat skladyvaetsya so skorost'yu vrasheniya Zemli $\vec v_E=\vec \Omega \times \vec r$. Vybiraya sootvetsvuyushie znaki mozhno eto ravenstvo zapisat' takzhe $v_E=\Omega r \cos \varphi$. Zdes' $\varphi$ - geocentricheskaya shirota, kotoraya mozhet byt' otozhdestvlena s obychnoi geograficheskoi shirotoi, poskol'ku szhatie Zemli malo $\sim 0.003$ i pri nashih vychisleniyah im mozhno prenebrech'.

V sisteme koordinat, kotoraya svyazana so centrom Zemli, kotoryi nahoditsya v sostoyanii svobodnogo padeniya v pole tyazhesti Solnca i planet, vremya otschityvaetsya sobstvennymi chasami $t$. V etoi zhe sisteme koordinat skorost' samoleta est':

\begin{displaymath} \vec V_a = \vec v_a + \vec \Omega \times r_a \end{displaymath}

Raznost' sobstvennogo vremeni dvuh chasov $\tau_1$ i $\tau_2$ opredelyaetsya ravenstvom:

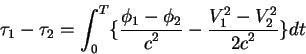
\begin{displaymath} \tau_1 - \tau_2 = \int_0^T \lbrace{\displaystyle\phi_1 - \ph... ...\displaystyle V_1^2 - V_2^2\over\displaystyle 2c^2}\rbrace d t \end{displaymath}

Podstavlyaya formulu dlya skorosti samoleta otnositel'no centra sistemy koordinat poluchaem, chto na bortu samoleta kotoryi letit na vostok, skorost' techeniya vremeni otlichaetsya ot skorosti techeniya vremeni na bortu samoleta, kotoryi letit na zapad. Eta raznost' sostavlyaet

\begin{displaymath} 2 v_{ae} \Omega r_a \cos \varphi \end{displaymath}

Zdes' $v_{ae}$ - komponenta skorosti samoleta, napravlennaya na vostok. Pri etom schitaetsya, chto skorosti samoleta, kotoryi letit na zapada i samoleta, letyashego na vostok ravny drug drugu.

Otsyuda vidno, chto predskazaniya obshei teorii otnositel'nosti byli podtverzhdeny s vysokoi (dlya togo vremeni) tochnost'yu.

Izmereniya vremennoi zaderzhki zavisyashei ot potenciala byli sdelany chetyre goda spustya [4]. Issledovateli sinhronizovali dvoe chasov, zatem pomestili odni chasy na vershinu gory, a vtorye ostavili na fizicheskom fakul'tete, raspolozhennom u podnozh'ya gory. Raznica v vysote sostavlyala 3250 m. Vremya za kotoroe izmeryalas' zaderzhka chasov sostavlyalo 66 dnei. Iz - za razlichiya v potenciale gravitacionnogo polya Zemli skorosti hoda chasov byli razlichny. Izmereniya opyat' podtverdili obshuyu teoriyu otnositel'nosti i izmerili zaderzhku s tochnost'yu $15\%$.

Dva goda spustya podobnyi eksperiment byl povtoren v Yaponii [5]. Issledovateli pomestili odni chasy na goru, a drugie pod goru. Raznica vysot sostavlyala 2818 m, a vremya izmereniya effekta bylo dve nedeli. Poskol'ku chasy, ispol'zuemye yaponskimi issledovatelyami byli znachitel'no tochnee, tochnost' izmerenii sostavlyala 5%. Vnov' predskazaniya obshei teorii otnositel'nosti byli podtverzhdeny.

Odni iz naibolee tochnyh izmerenii byli sdelany vo vremya vysotnogo poleta rakety [6]. Na bortu rakety nahodilsya vodorodnyi mazer, kotoryi ispol'zovalsya v kachestve vysokostabil'nyh chasov. Raketa podnyalas' na 10 000 m, a zatem upala v Atlanticheskii okean. Dlya izmerenii potencial'nogo chlena v zaderzhke chasov prishlos' kompensirovat' vklad dopplerovskogo chlena (raketa dvigalas' bystro), a takzhe ionosfernye effekty. Tem ne menee izmereniya byli blagopoluchno provedeny i pravil'nost' formuly dlya vremeni zaderzhki byla podtverzhdena s tochnost'yu 0.01%.

Izmereniya vremeni zaderzhki provodilis' takzhe pozzhe na samoletah. V polete osushestvlyalsya postoyannyi kontrol' hoda chasov i stabil'nosti parametrov. V chastnosti, byl proveden eksperiment po proverke "paradoksa bliznecov". Byli sinhronizovany chasy, posle chego odni chasy pomestili na bort samolet, a vtorye ostavili na Zemle. Chasy, kotorye nahodilis' na bortu samoleta, po priletu pokazali, chto na bortu proshlo bol'she vremeni, chem na Zemle!

V chem delo? Mozhet byt' obshaya teoriya otnositel'nosti neverna? Net, izmereniya vnov' polnost'yu podtverdili spravedlivost' obshei teorii otnositel'nosti, prosto nado delat' pravil'nye vyvody iz teoreticheskih polozhenii.

Klassicheskaya formulirovka paradoksa bliznecov otnosit'sya k sistemam koordinat, kotorye svobodny ot neodnorodnogo gravitacionnogo polya. Na Zemle, razumeetsya, neodnorodnoe gravitacionnoe pole prisutstvuet. Poetomu nado ne tol'ko sravnivat' zaderzhku vremeni voznikayushuyu na bortu samolet iz - za dvizheniya samolet, no takzhe i zaderzhku vremeni voznikayushuyu iz - za potencial'nogo chlena. Esli samolet dvizhetsya otnositel'no laboratorii (probnyh chasov), to chasy na ego bortu budut otstavat' ot chasov v laboratorii (eto effekt proporcional'nyi $-{\displaystyle v^2\over\displaystyle 2c^2}$), no samolet letit vyshe laboratorii, on letit v pole tyazhesti s oslablennym potencialom, a znachit, chasy, nahodyashiesya v laboratorii budut idti medlennee po sravneniyu s chasami, nahodyashimisya na bortu $+{\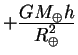displaystyle GM_{\oplus} h\over\displaystyle R^2_{\oplus}}$ (Zdes' $h$ -raznica vysot mezhdu samoletom i laboratoriei). Sravnit' vklad potencial'nogo chlena i chlena iz - za skorosti legko. Neobhodimo sravit' velichinu harakternoi skorosti v dannom potenciale (vtoraya kosmicheskaya skorost') s real'noi skorost'yu apparata.

Dlya samolet potencial'nyi chlen vsegda bol'she. Skorost' samolet znachitel'no men'she skorosti rakety, poetomu chasy, podnyatye na samolete nad laboratoriei (esli oni, konechno, podnyaty na dostatochno bol'shuyu vysotu) budut otstavat' po sravneniyu s chasami, nahodyashimisya v laboratorii.

Teper' formuly dlya izmeneniya tempa techeniya vremeni v zavisimosti ot skorosti i vysoty ispol'zuyutsya v navigacionnoi tehnologii GPS i GLONASS.

4.1.1 Paradoks bliznecov

Rassmotrim teper' "paradoks bliznecov" v ego klassicheskoi formulirovke. Itak, rassmatrivayutsya dvoe chasov, odni dlya prostoty budem oboznachat' $A$, vtorye $B$. Chasy $A$ vse vremya pokoyutsya otnositel'no inercial'noi sistemy koordinat $K$. Chasy $B$ vnachale tozhe pokoyutsya. Chasy sinhroniziruyutsya, zatem chasy $B$ nachinayut uskoryat'sya vdol' polozhitel'nyh znachenii osi $Ox$ sistemy koordinat $K$. Cherez nekotoroe vremya uskorenie propadaet i chasy $B$ po inercii dvizhutsya so skorost'yu $v$ vdol' osi $Ox$ nekotoroe vremya. Zatem chasy vnov' uskoryayutsya, no teper' v protivopolozhnom napravlenii, chto privodit k ih zamedleniyu i polnoi ostanovke, a zatem k nachalu dvizheniya v protivopolozhnom napravlenii. Chasy $B$ uskoryayutsya poka ne dostignut skorosti $-v$. Zatem chasy $B$ dvizhutsya v napravlenii k chasam $A$. V zaranee raschitannyi moment vremeni chasy $B$ vnov' nachinayut uskoryat'sya v napravlenii protivopolozhnom dvizheniyu tak, chtoby skorost' ih umen'shalas'. Uskorenie vnov' podbiraetsya tak, chtoby chasy $B$ okazalis' v odnoi tochke s chasami $A$ c nulevoi skorost'yu. Posle etogo pokazaniya chasov sravnivayutsya. Uskoreniya v etom myslennom eksperimente mozhno sdelat' dostatochno bol'shimi, tak chto vliyanie uchastkov dvizheniya s nenulevym uskoreniem na process vychisleniya zaderzhki chasov mozhno schitat' prenebrezhimo malym. Togda chasy $B$ dolzhny otstat' ot chasov $A$ na nekotoryi interval vremeni. Itak, dlya nablyudatelya, soputstvuyushego chasam $A$ dvizhushiesya chasy dolzhny otstat'.

Rassmotrim etot zhe process s tochki zreniya nablyudatelya soputstvuyushego chasam $B$. On imeet protivopolozhnye harakteristiki, tak chto s ego tochki zreniya "otstat'" dolzhny chasy $A$. Nizhe my proanaliziruem pravil'nyi hod rassuzhdenii i pokazhem, chto na samom dele dlya obeih nablyudatelei chasy $B$ dolzhny otstat' po sravneniyu s chasami $A$. Prichinoi nepravil'nyh rassuzhdenii yavlyaetsya nalichie polya uskoreniya v sisteme koordinat soputstvuyushei chasam $B$. Poetomu izmeneniya intervalov vremeni v sisteme soputstvuyushei $B$ nado schitat' uzhe po formulam obshei teorii otnositel'nosti, a ne tol'ko po formulam special'noi teorii otnositel'nosti.

Odno iz luchshih izlozhenii "paradaksa bliznecov" privel A.Einshtein v svoei populyarnoi stat'e "Dialog po povodu vozrazhenii protiv teorii otnositel'nosti" privedennoi v knige [7]. Budem sledovat' etomu izlozheniyu, podkreplyaya ego raschetami. Ves' process puteshestviya i vozvrasheniya chasov mozhno razdelit' na pyat' stadii.

S tochki zreniya $A$      S tochki zreniya $B$
1. Chasy $B$ uskoryayutsya vneshnimi silami v napravlenii polozhitel'nyh znachenii osi $Ox$, poka ne priobretut skorost' $v$. Chasy $A$ pokoyutsya.     1. V otricatel'nom napravlenii osi $Ox$ voznikaet gravitacionnoe pole, v kotorom $A$ padaet uskorenno. Chasy $B$ uderzhivayutsya vneshnimi silami v pokoe. Kogda $A$ priobretayut skorost' $v$ gravitacionnoe pole ischezaet.
2. Chasy $B$ dvizhutsya s postoyannoi skorost'yu do tochki 2. Chasy $A$ pokoyatsya.     2. Chasy $A$ dvizhutsya s postoyannoi skorost'yu do tochki $\hat 2$. Chasy $B$ pokoyatsya.
3. Chasy $B$ uskoryayutsya vneshnimi silami poka ne priobretut skorost' $-v$.     3. Poyavlyaetsya odnorodnoe pole tyazhesti napravlenoe v storonu polozhitel'nyh znachenii osi $Ox$, pod deistviem kotorogo $A$ uskoryayutsya v polozhitel'nom napravlenii do teh por poka ne priobretut skorost' $+v$. Posle etogo pole ischezaet. Vneshnie sily uderzhivayut chasy $B$.
4. Chasy $B$ dvizhutsya nazad s postoyannoi skorost'yu $v$, poka ne priblizyatsya k $A$. Chasy $A$ pokoyatsya.     4. Chasy $A$ dvizhutsya so skorost'yu $v$ v napravlenii polozhitel'nyh znachenii osi $Ox$, do teh por, poka ne priblizyatsya k $B$. Chasy $B$ ostayutsya v pokoe.
5. Chasy $B$ ostanavlivayutsya vneshnimi silami.     5. Voznikaet pole tyazhesti, kotoroe ostanavlivaet chasy $A$. Chasy $B$ uderzhivayutsya vneshnimi silami.

Kak vidim, dve sistemy koordinat neekvivalentny drug drugu. S tochki zreniya nablyudatelya soputsvuyushego chasam $A$ gravitacionnoe pole otsutstvuet, s tochki zreniya nablyudatelya soputstvuyushego chasam $B$ gravitacionnoe pole ne ravno nulyu. Dlya vychisleniya skorosti hoda chasov s tochki zreniya nablyudatelya $A$ dostatochno formul, vyvedennyh v ramkah STO, s tochki zreniya nablyudatelya $B$ pri vychislenii skorosti hoda vremeni neobhodimo uchityvat' effekty OTO.

Vnov' akkuratno uchityvaya raznicu mezhdu sistemami koordinat vychislim skorost' hoda chasov v sisteme $K$ i v sisteme $\hat K$ i sravnim kakie iz chasov otstanut' ot drugih.

Raschet budem vesti primenyaya priblizhennye formuly STO i OTO dlya togo, chtoby raschety byli legche i ne zatemnyalsya smysl formul, my budem schitat', chto skorost' $v$ znachitel'no men'she chem skorost' sveta.

Vnachale rasschitaem zaderzhku vremeni po formulam STO s tochki zreniya nablyudatelya soputstvuyushego chasam $A$. Budem schitat', chto vremya uskoreniya prenebrezhimo malo. Togda raznost' skorosti hoda chasov vo vremya pervoi stadii, a takzhe vo vremya tret'ei i pyatoi stadii pprenebrezhimo malo. Togda interval vremeni pokazannyi chasami v techenii vsego puteshestviya $B$ zavisit ot intervala vremeni pokazannomu chasami $A$ kak:

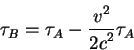
\begin{displaymath} \tau_B=\tau_A - {\displaystyle v^2\over\displaystyle 2c^2}\tau_A \end{displaymath}

Zdes' $\tau_A$ - polnoe vremya puteshestviya tuda - obratno.

Itak s tochki zreniya nablyudatelya soputstvuyushego chasam $A$ chasy $B$ otstayut.

Provedem raschet skorosti hoda obeih chasov s tochki zreniya nablyudatelya soputstvuyushego chasam $B$. Vo vremya pervoi stadii raznost' hoda prenebrezhimo mala. Oba chdena dayut prenebrezhimo malyi vklad. Potencial'nyi - potomu chto chasy $A$ i $B$ nahodyatsya prakticheski tol'ko v odnoi tochke, a vklad ot potencial'nogo chlena proporcionalen raznosti rasstoyanii, chlen zavisyashii ot skorosti tozhe mal.

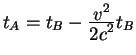Vo vremya vtoroi stadii dvizheniya po inercii, kotoraya dlitsya vremya, skazhem, $t_B$ chasy $A$ otstayut ot chasov $B$ kak $t_A=t_B -{\displaystyle v^2\over\displaystyle 2c^2}t_B$.

Budem schitat', chto tret'ya stadiya dlitsya interval vremeni $t_r$. Vo vremya tret'ei stadii vklad chlena proporcional'nogo skorosti chasov v raznost' hoda chasov prenebrezhimo mal. Odnako velik vklad potencial'nogo chlena. Deistvitel'no za vremya $t_B$ chasy $A$ proshli otnositel'no chasov $B$ rasstoyanie $L=vt_B$. Uskorenie, trebuemoe dlya izmeneniya skorosti s $+v$ na $-v$ v techenii vremeni $t_r$ sostavlyaet $g={\displaystyle 2v\over\displaystyle t_r}$.

Gravitacionnyi potencial mezhdu tochkami nahozhdeniya dvuh chasov sostavlyaet velichinu $\phi= +gL$. Znak plyus vybran potomu, chto uskorenie napravleno ot $A$ k $B$. Posle okonchaniya tret'ei stadii iz - za potencial'nogo chlena interval vremeni $T_A$ pokazannyi chasami $A$ i interval vremeni $T_B$ pokazannyi chasami $B$ svyazany ravenstvom

\begin{displaymath} T_A=T_B +\frac{gL}{c^2} t_r \end{displaymath}

Obratim vnimanie, chto vtoroe slagaemoe v etoi formule imeet polozhitel'nyi znak. Eto oznachaet, chto chasy $A$ teper' idut bystree, chem chasy $B$.

V techenii chetvertoi stadii chasy $A$ vnov' otstayut ot chasov $B$. Obratnyi put' dlitsya tot zhe interval vremeni $\hat t_B=t_B$. Za etot interval chasy $A$ vnov' otstayut. Interval vremeni, kotoryi pokazyvayut chasy $A$ sostavlyaet:

\begin{displaymath} \hat t_A=\hat t_B -\frac{v^2}{2c^2}\hat t_B \end{displaymath}

V techenii pyatoi stadii chasy $A$ vnov' zamedlyayutsya gravitacionnym polem. Odnako teper' raznost' hoda chasov $A$ i $B$ opyat' prenebrezhimo mala, po tem zhe prichinam, chto i na pervoi stadii.

Poschitaem polnyi interval vremeni, kotoryi pokazyvayut chasy $A$ s tochki zreniya nablyudatelya, soputstvuyushego chasam $B$. Promezhutok vremeni, kotoryi pokazyvayut chasy $A$ skladyvaetsya iz promezhutkov vremeni pokazyvaemyh etimi chasami s pervoi po pyatuyu stadii:

\begin{displaymath} \hat \tau_A=t_A +T_A +\hat t_A \end{displaymath}

Poetomu polnyi interval vremeni pokazannyi chasami $A$ s tochki zreniya nablyudatelya soputstvuyushego chasam $B$ est':

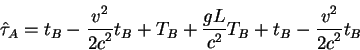
\begin{displaymath} \hat \tau_A=t_B -{\displaystyle v^2\over\displaystyle 2c^2}t... ...c^2} T_B + t_B -{\displaystyle v^2\over\displaystyle 2c^2}t_B \end{displaymath}

Podstavim znachenie polnogo vrmeni puteshestviya tuda - obratno $\tau_B=2t_B$. Krome togo, podstavim znacheniya $g={\displaystyle 2v\over\displaystyle T_B}$ i $L=vt_B$, vyrazhaya polnoe ravenstvo tol'ko cherez $v$. Okonchatel'no poluchaem, chto

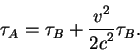
\begin{displaymath}\tau_A=\tau_B +{\displaystyle v^2\over\displaystyle 2c^2}\tau_B.\end{displaymath}

Teper' vidno, chto interval vremeni pokazyvaemyi chasami $A$ okazyvaetsya bol'she, chem interval vremeni pokazyvaemyi chasami $B$. Eto znachit, chto puteshestvuyushie chasy pokazhut men'shii promezhutok vremeni, chem chasy pokoyashiesya otnositel'no inercial'noi sistemy koordinat. Etot raschet demonstriruet otsutstvie "paradoksa bliznecov" v relyativistskoi fizike.


<< 3. Uskorennye sistemy otscheta | Oglavlenie | 5. Neevklidova geometriya >>

Publikacii s klyuchevymi slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni
Publikacii so slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni
Sm. takzhe:
Vse publikacii na tu zhe temu >>

Mneniya chitatelei [21]
Ocenka: 3.1 [golosov: 132]
 
O reitinge
Versiya dlya pechati Raspechatat'

Astrometriya - Astronomicheskie instrumenty - Astronomicheskoe obrazovanie - Astrofizika - Istoriya astronomii - Kosmonavtika, issledovanie kosmosa - Lyubitel'skaya astronomiya - Planety i Solnechnaya sistema - Solnce

Astronet | Nauchnaya set' | GAISh MGU | Poisk po MGU | O proekte | Avtoram

Kommentarii, voprosy? Pishite: info@astronet.ru ili syuda

Rambler's Top100 Yandeks citirovaniya