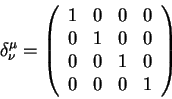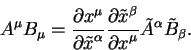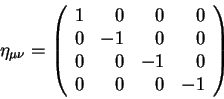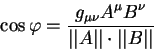<< 4. Eksperimenty po OTO | Oglavlenie | 6. Analiz v neevklidovoi >>
5. Neevklidova geometriya
V klassicheskoi fizike prostranstvo bylo evklidovym, a vremya absolyutnym i edinym dlya vsego prostranstva. V relyativistskoi fizike, kak my uzhe ubedilis' iz materiala predydushei glavy prostranstvo yavlyaetsya neevklidovym. V obshem sluchae geometriya predstavlyaet iz sebya chetyrehmernoe differenciruemoe mnogoobrazie,
V proizvol'noi geometrii rassmatrivayutsya proizvol'nye preobrazovaniya
koordinat:
naprimer,

kak vidno iz privedennyh preobrazovanii, oni opisyvayut prosto perehod ot sfericheskih k dekartovym koordinatam.
Differencial v netil'dovannoi sisteme svyazan s differencialom v sisteme
koordinat s til'doi uravneniyami vida:
V geometrii vvoditsya ponyatie geometricheskogo ob'ekta. Ne perechislyaya vseh ob'ektov geometrii nazovem tol'ko skalyary, vektory i tenzory. Strogo govorya, vse perechislennye velichiny yavlyayutsya tenzorami, tak skalyar yavlyaetsya tenzorom nulevogo ranga, a vektor tenzorom pervogo ranga. Odnako istoricheski prinyato vydelyat' skalyary i vektory.
Skalyarnaya velichina (ili skalyar) pri preobrazovaniyah sistemy koordinat ne
preobrazuetsya,
Vektorom nazyvaetsya velichina, kotoraya soderzhit chetyre komponenty,
preobrazuemye soglasno pravilu:
dlya kontravariantnyh komponent i
dlya kovariantnyh komponent.
Kak mozhno zametit', iz zakona preobrazovaniya (5.1) preobrazovanie kontravariantnyh komponent kakogo - libo vektora podobno preobrazovaniyu differencialov koordinat, predstavlyayushih raznost' polozhenii dvuh tochek. Sledovatel'no kontravariantnye komponenty vektora mozhno predstavit' kak sistemu iz dvuh tochek, s ukazaniem kakaya iz tochek yavlyaetsya pervoi, a kakaya yavlyaetsya vtoroi. Primerom kontravariantnyh komponent yavlyaetsya chetyrehmernaya skorost' kakogo - libo tela.
Primerom kovariantnyh komponet vektora yavlyaetsya gradient nekotorogo polya:
Obrazom gradienta ot polya yavlyayutsya nabory dvumernyh poverhnostei
opredelyayushih postoyanstvo polya
![]() . Sledovatel'no
geometricheskim obrazom kovariantnyh komponent tenzora yavlyayutsya dvumernye
poverhnosti "raskrashennye" v razlichnye "cveta" dlya togo, chtoby opredelit'
kakaya iz poverhnostei yavlyaetsya pervoi, a kakaya - vtoroi.
. Sledovatel'no
geometricheskim obrazom kovariantnyh komponent tenzora yavlyayutsya dvumernye
poverhnosti "raskrashennye" v razlichnye "cveta" dlya togo, chtoby opredelit'
kakaya iz poverhnostei yavlyaetsya pervoi, a kakaya - vtoroi.
Vypishem takzhe pravilo po kotoromu preobrazuyutsya komponenty tenzora vtorogo
ranga:

Geometricheskaya velichina
![]() , kotoraya imeet
, kotoraya imeet ![]() verhnih ipndeksov i
verhnih ipndeksov i ![]() nizhnih
indeksov i preobrazuetsya po zakonu:
nizhnih
indeksov i preobrazuetsya po zakonu:
nazyvaetsya tenzorom ranga ![]() s
s ![]() kontravariantnymi
kontravariantnymi ![]() kovariantnymi
indeksami.
kovariantnymi
indeksami.
V algebre tenzorov opredelyaetsya summirovanie tenzorov odinakovogo ranga i s
odinakovo raspolozhennymi indeksami:
umnozhenie opredeleno dlya tenzorov lyubogo ranga s proizvol'no raspolozhennymi
indeksami:
V tenzornoi algebre opredelyayut takzhe svertku dvuh tenzorov po pravilu:
dlya proizvol'nogo raspolozheniya indeksov vazhno tol'ko, chtoby indeks po
kotoromu provoditsya svertka v pervom tenzore byl verhnim, vo vtorom -
nizhnim (ili naoborot, v pervom - nizhnim, a vo vtorom -verhnim). Polozhenie i
kolichestvo ostal'nyh indeksov perenositsya v svertku po ih mestu. Svertki
mogut byt' obrazovany razlichnymi sposobami, odnako kazhdoe summirovanie
dolzhno vypolnyat'sya po verhnemu i nizhnemu indeksu. Naprimer, summa

ne yavlyaetsya tenzorom, kak legko ubedit'sya rassmotrev zakon preobrazovaniya etoi velichiny.
V sovremennoi tenzornoi algebre, analize i fizike pol'zuyutsya pravilom
summirovaniya Einshteina, kotoryi dlya udobstva vvel sledushee oboznachenie:
pri etom indeks ![]() nazyvayut mertvym indeksom i po povtoryayushimsya
indeksam proizvoditsya summirovanie. Tak zapis'
nazyvayut mertvym indeksom i po povtoryayushimsya
indeksam proizvoditsya summirovanie. Tak zapis'
![]() oboznachaet:
oboznachaet:
Povsyudu v etoi knige my budem ispol'zovat' eto pravilo, dva povtoryayushihsya indeksa odin verhnii, drugoi - nizhnii budet oznachat', chto po nim proizvoditsya summirovanie.
Opredelim takzhe obratnye tenzory soglasno uravneniyu:
Zdes'
![]() - simvol Kronekera, kotoryi opredelyaetsya
sledushimi usloviyami
- simvol Kronekera, kotoryi opredelyaetsya
sledushimi usloviyami
![]() esli
esli ![]() i
i
![]() esli
esli ![]() . Mozhnl takzhe vypisat' matricu
simvola Kronekera
. Mozhnl takzhe vypisat' matricu
simvola Kronekera
Svertka dvuh tenzorov ponizhaet rang proizvedeniya. Tak, vazhnyi primer
pokazyvaet, chto proizvedenie kovariantnyh komponent vektora na
kontravariantnye komponenty yavlyaetsya invariantom:
Razlichnye avtory [8], [9], [12] vvodyat takzhe operaciyu simmetrirovaniya, albternirovaniya, vyklyucheniya indeksov i t.p. Dlya nas vazhnoi ostaetsya tol'ko poslednyaya operaciya nad tenzorami - obrazovanie sleda, obrazovanie poperechnoi chasti tenzora i obrazovanie poperechno - bessledovoi chasti tenzora, kotorye budut primenyat'sya vo vtoroi chasti knigi. Odnako dlya ih opredeleniya nam pridetsya ispol'zovat' metriku, poetomu otlozhim vvedeniya etih ponyatii posle obsuzhdeniya metriki.
5.1 Metrika iskrivlennogo prostranstva - vremeni
Geometriya chetyrehmernogo prostranstva - vremeni polnost'yu opredelyaetsya desyat'yu funkciyami, kotorye yavlyayutsya komponentami simmetrichnogo tenzora vtorogo ranga. Metrika chetyrehmernogo intervala est':
Zdes' ![]() - kovariantnye komponenty metricheskogo tenzora ili, kak
obychno govoryat, metricheskii tenzor vtorogo ranga.
- kovariantnye komponenty metricheskogo tenzora ili, kak
obychno govoryat, metricheskii tenzor vtorogo ranga.
Komponenty metricheskogo tenzora yavlyayutsya, voobshe govorya, funkciyami vseh chetyreh koordinat.
Preobrazovaniem koordinat vsegda mozhno dobit'sya togo, chtoby komponenty
metricheskogo tenzora byli privedeny k vidu metriki Minkovskogo:
V prostranstve s zadannoi metrikoi mozhno opredelit' svyaz' mezhdu
kovariantnymi i kontravariantnymi komponentami tenzorov, tak dlya vektora
svyaz' mezhdu etimi komponentami zadaetsya uravneniyami:
Teper' mozhno opredelit' normu vektora, analogichno tomu, kak eto delaetsya v
evklidovoi geometrii. Noromoi vektora po opredeleniyu polagayut velichinu
[8], [9], [12]:
V zavisimosti ot togo, chemu ravna norma vetora ego nazyvayut:
- vremenipodobnym, esli
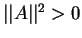
- prostranstvennopodobnym, esli
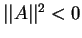
- izotropnym, esli
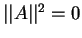
Norma nazyvaetsya takzhe dlinoi vektora. Kak vidno iz opredeleniya izotropnogo vektora on obladaet nulevoi dlinoi.
Rassmotrim svertku dvuh vektorov. Dva vektora, kotorye udovletvoryayut
usloviyu:
nazyvayutsya ortogonal'nymi. Otsyuda mozhno sdelat' vyvod, chto izotropnyi vektor ortogonalen samomu sebe i lyubomu drugomu izotropnomu vektoru. Sleduet zametit', chto takim svoistvom obladayut tol'ko izotropnye vektora.
Krome etogo vazhnogo svoistva privedem takzhe uravnenie opisyvayushee ugol
![]() mezhdu dvumya vektorami
mezhdu dvumya vektorami ![]() i
i ![]() v neevklidovoi
geometrii:
v neevklidovoi
geometrii:
Zdes' sleduet zametit', chto oba vektora ![]() i
i ![]() yavlyayutsya libo
prostranstvennopodobnymi, libo izotropnymi.
yavlyayutsya libo
prostranstvennopodobnymi, libo izotropnymi.
5.1.1 Primery metriki iskrivlennogo prostranstva
Privedem primery metriki iskrivlennogo prostranstva. Na samom dele v bytu my stalkivaemsya s primera geometrii iskrivlennogo prostranstva znachitel'no chashe, chem privykli dumat'. Poverhnost' myacha, poverhnost' spinki kresla, poverhnost' kuvshina ili grafina - vot nepolnyi spisok dvumernyh iskrivlennyh prostranstv. Primery ideal'nyh ploskostei, takih kak kryshka stola ili rovnyi listok bumagi v etom ryadu vyglyadyat, skoree isklyucheniyami, chem pravilom.
Privedem v kachestve primera metriku na poverhnosti sfery. Dlya etogo vypishem
vnachale metriku evklidova prostranstva v sfericheskoi sisteme koordinat:
Budem schitat', chto my vychislyaem rasstoyanie tol'ko mezhdu temi tochkami,
kotorye lezhat na poverhnosti sfery radiusa ![]() . Togda mozhno polagat', chto
. Togda mozhno polagat', chto
![]() , a znachit metrika poluchaet vid:
, a znachit metrika poluchaet vid:
teper' metrika opisyvaet poverhnost' sfery, a geometriya, kotoruyu opisyvaet dannyi metricheskii tenzor yavlyaetsya neevklidovoi.
5.2 Geodezicheskie linii v neevklidovoi geometrii
V evklidovoi geometrii ochen' vazhnym ponyatiem yavlyaetsya pryamaya mezhdu dvumya tochkami, kotoraya k tomu zhe yavlyaetsya kratchaishim rasstoyaniem mezhdu etimi tochkami. V neevklidovoi geometrii ponyatie pryamoi zamenyaetsya ponyatiem geodezicheskoi linii, kotoraya yavlyaetsya ekstremal'nym putem mezhdu dvumya tochkami.
Dlya nahozhdeniya uravneniya geodezicheskoi liniii primenim variacionnoe ischislenie.
Dlina linii v geometrii obshei teorii otnositel'nosti est' integral po
intervalu mezhdu dvumya sobytiyami razdelennymi po vremeni i prostranstvu:
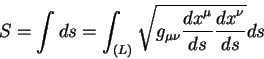
Linii ekstremal'nogo puti udovletvoryaet usloviyu:
Zdes' simvol ![]() oznachaet pervuyu variaciyu. Iz etogo usloviya
poluchaetsya uravnenie geodezicheskoi linii.
oznachaet pervuyu variaciyu. Iz etogo usloviya
poluchaetsya uravnenie geodezicheskoi linii.
Dlya vychisleniya variacii velichiny ![]() primenim sledushii priem.
Provar'iruem ne differencial intervala
primenim sledushii priem.
Provar'iruem ne differencial intervala ![]() , a kvadrat differenciala
, a kvadrat differenciala
![]() . Variacii samogo differenciala po variaciyam kvadrata mozhno poluchit'
soglasno uravneniyu
. Variacii samogo differenciala po variaciyam kvadrata mozhno poluchit'
soglasno uravneniyu
![]() . S drugoi storony,
variacii kvadrata
. S drugoi storony,
variacii kvadrata ![]() est':
est':
pravuyu chast' etogo ravenstva mozhno predstavit' v vide summy:
Vospol'zuemsya ravenstvami
![]() i
i
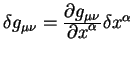 i poluchim uravnenie dlya variacii differenciala intervala:
i poluchim uravnenie dlya variacii differenciala intervala:
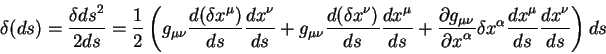
Tretii chlen v kruglyh skobkah uzhe priveden k vidu prigodnomu dlya vychisleniya
pervoi variacii. Dlya privedeniya k takomu zhe vidu pervyh dvuh chlenov
vospol'zuemsya ravenstvom:
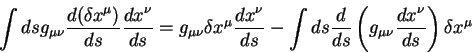
Vospol'zuemsya teper' etimi ravenstvami i vychislim pervuyu variaciyu polnogo
puti:
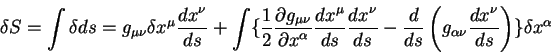
V etom uravnenii pervyi chlen posle vtorogo znaka ravenstva predstavlyaet iz
sebya variacii v konechnyh tochkah puti, po opredeleniyu eti variacii ravny
nulyu [13], [14]. Chlen pod znakom integrala v figurnyh skobkah
dolzhen obrashat'sya v nul' na geodezicheskoi linii. Eto i daet nam uravnenie
geodezicheskoi linii:
Zdes' ![]() - vektor kasatel'nyi k geodezicheskoi linii.
- vektor kasatel'nyi k geodezicheskoi linii.
Uravnenie, kotoroe my poluchili yavlyaetsya uravneniem vtorogo poryadka. V
sluchae evklidovoi geometrii, kogda vse komponenty metricheskogo tenzora
yavlyayutsya diagonal'nymi i ravny edinice, pravaya chast' ravenstva
(5.10) ravna nulyu. Togda reshenie etogo uravneniya est'
![]() . Eto reshenie opisyvaet pryamye linii, kotorye yavlyayutsya liniyami
kratchaishego puti v evklidovoi geometrii.
. Eto reshenie opisyvaet pryamye linii, kotorye yavlyayutsya liniyami
kratchaishego puti v evklidovoi geometrii.
Privedem eto uravnenie k standartnoi forme, prinyatoi v neevklidovoi
geometrii. Dlya etogo vospol'zuemsya tozhdestvom:
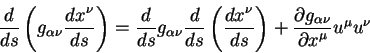
Podstaviv ego v levuyu chast' uravneniya (5.10) poluchaem uravnenie
vida:
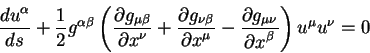
Velichina
nazyvaetsya simvolom Kristoffelya. Simvol Kristoffelya imeet tri indeksa i ne yavlyaetsya tenzorom. V algebre takie velichiny nosyat nazvanie simvoly pervogo roda.
Standartnyi vid uravneniya geodezicheskoi linii v neevklidovoi geometrii
zapisyvaetsya s pomosh'yu simvola Kristoffelya:
Krome etogo, standartnogo vida uravneniya geodezicheskoi linii, mozhno takzhe
zapisat' kak menyaetsya differencial kasatel'nogo vektora ![]() pri
perenose vdol' geodezicheskoi linii:
pri
perenose vdol' geodezicheskoi linii:
5.2.1 Geodezicheskie linii na poverhnosti sfery
Rassmotrim v kachestve primera geodezicheskie linii na sfere - dvumernoi
neevklidovoi poverhnosti. Metricheskii tenzor na poverhnosti sfery imeet
vid:
Kontravariantnye komponenty metricheskogo tenzora na poverhnosti sfery est':
Vychislyaya simvol Kristoffelya poluchaem, chto vse komponenty ravny nulyu za
isklyucheniem dvuh:

Uravneniya geodezicheskih linii imeyut vid:
i
Zdes' ![]() ,
, ![]() sfericheskie koordinaty nakloneniya i azimuta, a
sfericheskie koordinaty nakloneniya i azimuta, a
![]() - afinnyi parametr vdol' geodezicheskoi linii.
- afinnyi parametr vdol' geodezicheskoi linii.
Pri privedenii k pervomu integralu uravnenie (5.17) poluchaet vid:
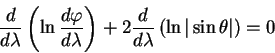
ili
Zdes'
 oboznachaet konstantu
integrirovaniya. Pervyi integral uravneniya (5.16) mozhno legko
privesti k udobnoi forme, esli vybrat' v kachestve afinnogo parametra dlinu
vdol' geodezicheskoi
oboznachaet konstantu
integrirovaniya. Pervyi integral uravneniya (5.16) mozhno legko
privesti k udobnoi forme, esli vybrat' v kachestve afinnogo parametra dlinu
vdol' geodezicheskoi
![]() . Togda integral pervogo uravneniya
stanovitsya:
. Togda integral pervogo uravneniya
stanovitsya:
Rassmotrim dva chastnyh sluchaya geodezicheskih linii.
Dvizhenie po ekvatoru
Pust' nasha liniya nachinaetsya na ekvatore
![]() , prichem
napravlenie etoi linii sovpadaet s napravleniem ekvatora, t.e.
, prichem
napravlenie etoi linii sovpadaet s napravleniem ekvatora, t.e.
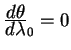 i
i
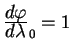 .
.
Reshenie dlya geodezicheskoi linii poluchaetsya iz uravnenii (5.18,
5.19). Deistvitel'no, pravaya chast' ravenstva (5.18)
est' 1. Podstavlyaem vyrazhenie dlya
![]() v
uravnenie (5.19) i poluchaem uravnenie:
v
uravnenie (5.19) i poluchaem uravnenie:
Udovletvoryaet etomu uravneniyu tol'ko znacheniya
![]() .
Takim obrazom dokazano, chto ekvator yavlyaetsya geodezicheskoi liniei na sfere.
.
Takim obrazom dokazano, chto ekvator yavlyaetsya geodezicheskoi liniei na sfere.
Dvizhenie po meridianu
Rassmotrim teper' dvizhenie vdol' meridiana i pokazhem, chto meridian takzhe
yavlyaetsya geodezicheskoi liniei. Teper' vektor, kasatel'nyi k linii imeet
komponenty:
Nachal'nuyu tochku takzhe vyberem na ekvatore
![]() . Iz
uravneniya (5.18) poluchaem, chto
. Iz
uravneniya (5.18) poluchaem, chto
otkuda sleduet, chto
![]() . Iz vtorogo integrala
sistemy (5.19) poluchaem, chto
. Iz vtorogo integrala
sistemy (5.19) poluchaem, chto
otkuda neposredstvenno sleduet, chto
Ne rassmatrivaya obshego sluchaya resheniya sistemy (5.18, 5.19) upomyanem tol'ko, chto ekvator i meridian na poverhnosti sfery yavlyayutsya chastnymi sluchayami bol'shogo kruga - secheniya poverhnosti sfery ploskost'yu, kotoraya prohodit cherez centr sfery. Rassmatrivaya trehmernye vrasheniya, mozhno pokazat', chto tol'ko otrezok bol'shogo kruga na sfere predstavlyaet kusok geodezicheskoi linii. Polnaya geodezicheskaya liniya predstavlyaet iz sebya bol'shoi krug.
Dvizhenie po malomu krugu
Prodemonstriruem otlichie proizvol'noi linii ot geodezicheskoi linii na primere malogo kruga na sfere. Malyi krug na sfere - eto sechenie sfery ploskost'yu, kotoraya ne prohodit cherez centr sfery.
Vyberem malyi krug tak, chtoby on byl secheniem s
![]() . Togda
uravneniya, kotorye opisyvayut malyi krug est':
. Togda
uravneniya, kotorye opisyvayut malyi krug est':
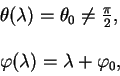
otsyuda legko naiti pervye i vtorye proizvodnye ot koordinat po afinnomu
parametru:
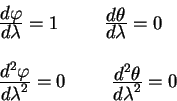
Podstavlyaya eti znacheniya v uravneniya geodezicheskih prihodim k protivorechiyu:
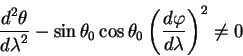
Takim obrazom malyi krug na sfere ne yavlyaetsya geodezicheskoi liniei.
<< 4. Eksperimenty po OTO | Oglavlenie | 6. Analiz v neevklidovoi >>
|
Publikacii s klyuchevymi slovami:
Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni
Publikacii so slovami: Obshaya teoriya otnositel'nosti - special'naya teoriya otnositel'nosti - sistemy otscheta - izmerenie vremeni | |
Sm. takzhe:
Vse publikacii na tu zhe temu >> | |